文章目录
1. 雷达的基本概念
无线电探测及测距(Radio Detection and Ranging), 发射电磁波并接收目标反射的回波信号,通过对比发射信号与回收信号,获取目标的位置、速度等信息。
1.1 毫米波雷达分类
雷达的分类
• 所发射电磁波的频段,决定了雷达的基本性能特点
• 超视距雷达、微波雷达、毫米波雷达、激光雷达、…
- 按照用途分类:军用,气象,导航,车载
- 按照波长分类:米,分米,厘米,毫米
- 按照波形分类:脉冲,连续波
按照波长和用途分类
- 长波雷达(米,分米),分辨率低,穿透性强 ➢一般用于广播,军事预警,卫星通讯等:
- 短波雷达(厘米,毫米),分辨率高,穿透性差 ➢一般用于测绘,短程通讯,车载应用等
按照波形分类
- 脉冲雷达 ➢通过脉冲发送和接收的时间差来确定目标的距离 ➢不能确定目标的速度
- 连续波雷达 ➢发射信号在时间上是连续的 ➢发射信号的频率是随着时间变化的(调频连续波)
1.2 信息的传输
◼ 调制:将调制信号(待传输信息)混合到载波信号(起到载运作
用的信号)的过程,可分为调频,调幅,调相。
◼ 解调:相反的过程,即从混合信号中恢复出待传输信息。
◼ 带宽:调制信号频谱的宽度,带宽高有利于传输更多数据。
- 毫米波雷达使用的电磁波波长介于1-10mm,波长短、频段宽,比较 容易实现窄波束,雷达分辨率高,不易受干扰
- 早期被应用于军事领域,随着雷达技术的发展与进步,毫米波雷达传 感器开始应用于汽车电子、无人机、智能交通等多个领域。

1.3 毫米波雷达的信号频段
频率24GHz77GHz探测范围 探测距离短,探测角度(FOV)大探测距离长,探测角度小频段限制24GHz频段因与其他无线电设备共享,必须限制发射功率独占频段带宽小于1GHz可达4GHz优势在中短距测距有明显优势;探测范围FOV更大波长更短波束更窄;识别精度高且穿透力更强;带宽更大可兼顾远中近不同场景代表产品大陆 ARS208,Hella 24GHz角雷达大陆 ARS408,BOSCH LRR4
1.4 毫米波雷达工作原理
在车载毫米波雷达中,目前主要有三种调制方案:调频连续波(Frequency
Modulated Continuous Wave, FMCW),频移键控(Frequency Shift Keying, FSK)以及相移键控(Phase Shift Keying, PSK)。
主流车载毫米波雷达所采用的的调制信号为调频连续波FMCW。
其基本原理是在发射端发射一个频率随时间变化的信号,经目标反射后被接收机接收,通过反射信号和接收信号之间的混频,得出两个信号的频率差,随后通过电磁波传播公式和多普勒效应公式求出目标距离和速度.
⚫ 测距测速是通过分析发射和接收的调频连续之间的区别来实现
⚫ 测量角度是通过计算不同天线单元之间的延时差来计算
1.4.1 毫米波雷达测速测距的数学原理

这里首先分析
0
<
t
<
T
/
2
0<t<T/2
0<t<T/2 时收发信号的关系。在调频连续波雷达中,本振信号的频率在半个周期内是随**时间成线性关系变化**的,即
f
L
O
(
t
)
=
f
0
+
k
t
(
0
<
t
<
T
2
)
{f_{LO}}(t) = {f_0} + kt{\rm{ }}(0 < t < \frac{T}{2})
fLO(t)=f0+kt(0<t<2T) 其中
f
0
f_0
f0 是初始时刻的频率,
k
k
k 是频率随时间变化的斜率。因为频率是相位关于时间
t
t
t 的导数,因此相位可以表示为频率关于时间
t
t
t 的积分,即
ϕ
(
t
)
=
2
π
∫
f
(
t
)
d
t
=
π
k
t
2
+
2
π
f
0
t
+
ϕ
0
\phi (t) = 2\pi \int {f(t)dt = \pi k{t^2} + 2\pi {f_0}t + {\phi _0}}
ϕ(t)=2π∫f(t)dt=πkt2+2πf0t+ϕ0 其中
ϕ
0
\phi _0
ϕ0 是初始相位,因此本振信号关于时间的表达式可以写成
V
L
O
(
t
)
=
V
1
cos
(
π
k
t
2
+
2
π
f
0
t
+
ϕ
0
)
{V_{LO}}(t) = {V_1}\cos (\pi k{t^2} + 2\pi {f_0}t + {\phi _0})
VLO(t)=V1cos(πkt2+2πf0t+ϕ0) 其中
V
1
V_1
V1 是本振信号的幅度,由于该本振信号的**频率是随时间呈连续周期性变化**的,所以称之为调频连续波,本振信号经过功率放大器(Power Amplifier, PA)放大后,由天线发射到自由空间中,这里把 PA 和天线的总增益记为
G
1
G_1
G1,则发射信号为
V
T
X
(
t
)
=
G
1
V
1
cos
(
π
k
t
2
+
2
π
f
0
t
+
ϕ
0
)
{V_{TX}}(t) = {G_1}{V_1}\cos (\pi k{t^2} + 2\pi {f_0}t + {\phi _0})
VTX(t)=G1V1cos(πkt2+2πf0t+ϕ0) 该信号经过空气传播到目标表面,被目标反射,最后由接收机接收,信号往返的传播时间为
τ
τ
τ,若雷达和目标的距离为
r
(
t
)
r(t)
r(t),则
τ
=
2
r
(
t
)
c
=
2
(
r
0
+
v
t
)
c
\tau = \frac{{2r(t)}}{c} = \frac{{2({r_0} + vt)}}{c}
τ=c2r(t)=c2(r0+vt) 其中
c
c
c 为电磁波在空气中的传播速度,
r
0
r_0
r0 是初始距离,
v
v
v 为雷达和目标间的相对速度。
电磁波在空气中传播和被目标反射的过程也会带来一定损耗,损耗系数记作
α
1
α_1
α1,则接收信号可以表示为
V
R
X
(
t
)
=
α
1
G
1
V
1
cos
(
π
k
(
t
−
τ
)
2
+
2
π
f
0
(
t
−
τ
)
+
ϕ
0
)
{V_{RX}}(t) = {\alpha _1}{G_1}{V_1}\cos (\pi k{(t - \tau )^2} + 2\pi {f_0}(t - \tau ) + {\phi _0})
VRX(t)=α1G1V1cos(πk(t−τ)2+2πf0(t−τ)+ϕ0) 这里再介绍以下混频的概念:
混频:输出信号频率等于两输入信号频率之和、差或其他组合的电路。
常用方法:
cos
α
⋅
cos
β
=
[
cos
(
α
+
β
)
+
cos
(
α
−
β
)
]
/
2
\cos \alpha \cdot \cos \beta = [\cos (\alpha + \beta ) + \cos (\alpha - \beta )]/2
cosα⋅cosβ=[cos(α+β)+cos(α−β)]/2
接收信号经过低噪声放大器(Low Noise Amplifier, LNA)放大后,与本振信号进行混频。混频后的信号包含了高频分量和低频分量,将该信号通过一个低通滤波器可得(假设通带内的增益为单位增益):
V
I
F
(
t
)
=
α
1
G
1
G
2
V
1
2
cos
(
2
π
k
τ
t
+
2
π
f
0
τ
−
π
k
τ
2
)
{V_{IF}}(t) = {\alpha _1}{G_1}{G_2}{V_1}^2\cos (2\pi k\tau t + 2\pi {f_0}\tau - \pi k{\tau ^2})
VIF(t)=α1G1G2V12cos(2πkτt+2πf0τ−πkτ2) 求导,即可求出中频频率(混频后的信号经低通滤波后所得低频分量,又叫中频频率
f
𝐼
𝐹
f_{𝐼𝐹}
fIF(intermediate frequency)为,是RX与TX之差。)
f
I
F
(
t
)
≈
2
k
r
0
c
+
2
f
0
v
c
{f_{IF}}(t) \approx \frac{{2k{r_0}}}{c} + \frac{{2{f_0}v}}{c}
fIF(t)≈c2kr0+c2f0v 只知道上式是无法求出速度和距离的,所以需要用到三角波的原理进行求解,三角波有两个斜率,一正一负,可以得到两个表达式,进而可以求解出距离
r
r
r和速度
v
v
v。三角波的周期为
T
T
T,最低频率、最高频率和中心频率分别为
f
a
、
f
b
、
f
c
f_a、f_b、f_c
fa、fb、fc,其带宽
B
=
f
b
−
f
a
B=f_b-f_a
B=fb−fa,三角波的斜率为
k
=
2
B
T
=
2
(
f
b
−
f
a
)
T
k = \frac{{2B}}{T} = \frac{{2({f_b} - {f_a})}}{T}
k=T2B=T2(fb−fa) 上升、下降区间的中频频率分别为
𝑓
1
𝑓_1
f1,
𝑓
2
𝑓_2
f2,斜率为
k
k
k, 光速为
c
c
c,变频后的结果如下
f
1
=
2
k
r
c
+
2
f
c
v
c
{f_1} = \frac{{2kr}}{c} + \frac{{2{f_c}v}}{c}
f1=c2kr+c2fcv
f
2
=
−
2
k
r
c
+
2
f
c
v
c
{f_2} = \frac{{ - 2kr}}{c} + \frac{{2{f_c}v}}{c}
f2=c−2kr+c2fcv 因此可以解出速度和距离
v
=
(
f
1
+
f
2
)
c
4
f
c
v = \frac{{({f_1} + {f_2})c}}{{4{f_c}}}
v=4fc(f1+f2)c
r
=
(
f
1
−
f
2
)
c
4
k
r = \frac{{({f_1} - {f_2})c}}{{4k}}
r=4k(f1−f2)c
1.4.2 毫米波雷达测角度的数学原理
一对收发机所采集到的信号是不具备角度信息的, 因此需要采用多路发射多路接收的架构,或者采用相控阵架构。
短波长和小天线孔径就很有必要了,
•短波长意味着波束更窄,能量更加集中;
•更小的孔径尺寸意味着系统上能集成更多的天线单元
这些都有利于提高角分辨率。
天线阵列示意图
1.4.3 硬件接口
⚫ 天线向外发射毫米波,接收目标反射信号
⚫ 信号处理器完成回波信号处理
⚫ 算法芯片完成原始点云目标的进一步处理
⚫ CAN接口完成毫米波处理数据的发送以及配置信息的输入
1.4.4 关键零部件
毫米波雷达的天线接发系统
• PCB板实现MMIC(单片微波集成电路)
• 包括接收电路单元,负责发射与接收连续调频波
毫米波雷达的信号处理芯片
• 包含信号处理器和算法芯片
• 完成回波信号处理与目标感知结果的计算
1.4.5 数据的协议与格式
传输层协议:网口UDP/IP协议,或者CAN接口
- 控制器局域网总线(CAN,Controller Area Network)是一种用 于实时应用的串行通讯协议总线
数据格式:按照CAN编码机制,确定雷达的输入配置信息与输出数据格式
- CAN报文 13个字节 信息段(5Byte)+数据段(8Byte) 数据段按照事先规定好的报文规则进行编码和解码
- CAN报文解析使用方法
 数据内容:不同内容使用不同的CAN协议 Cluster类型:包含3类message:
数据内容:不同内容使用不同的CAN协议 Cluster类型:包含3类message: - Header(数量n)
- +n个数据消息(距离/角度/速度)
- +n个质量消息(数据的方差)(1≤n ≤ 256)
1.5 车载毫米波雷达的重要参数
常见参数:
- 测量性能 测距范围 距离/水平角/速度 分辨率 (可对两个物体进行区分的最小单位) 距离/水平角/速度 精度 (测量不确定性)
- 操作条件 雷达发射功率、传输能力、电源、功耗、操作温度
1.6 车载毫米波雷达的三种典型应用

毫米波雷达具有全天侯适应性,是高级别自动驾驶实现必备的环境感知传感器.
77GHz及79GHz雷达是未来车载毫米波雷达的发展方向,国内正处于快速追赶时期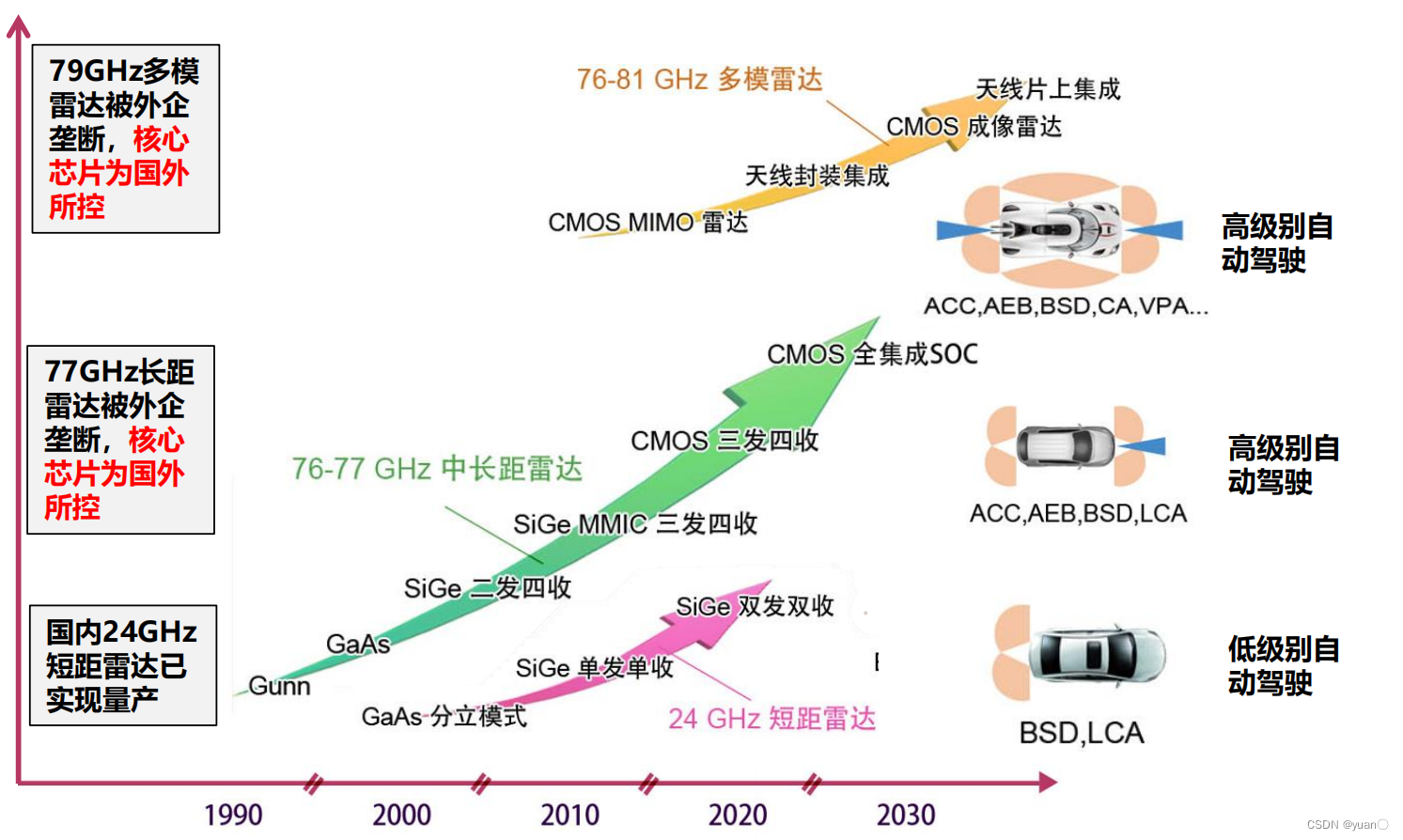
2. FMCW雷达的工作流程
PS:此部分主要是为了简单理解FMCW雷达的工作原理,是对第一章内容的补充。
总结一下,FMCW雷达的工作流程:
- 合成器生成一个线性调频信号 ;
- 发射天线( TX )发射线性调频信号;
- 接收天线( RX )捕获目标对线性调频信号的反射;
- 混频器将RX和TX信号合并到一-起,生成一个中频(IF )信号。

2.1 线性调频脉冲信号
对于一个脉冲信号
- 信号的频率随时间的变化线性升高
- 起始频率 f c f_c fc,持续时间 T c T_c Tc,带宽 B B B,频率变化率 S S S

2.2 混频器
作用:将TX和RX的信号合并生成一个新的信号IF
TX发射信号:
x
1
=
sin
(
2
π
f
1
t
+
ϕ
1
)
{x_1} = \sin (2\pi {f_1}t + {\phi _1})
x1=sin(2πf1t+ϕ1)
RX接收信号:
x
2
=
sin
(
2
π
f
2
t
+
ϕ
2
)
{x_2} = \sin (2\pi {f_2}t + {\phi _2})
x2=sin(2πf2t+ϕ2)
中频信号IF:
x
o
u
t
=
sin
(
2
π
(
f
1
−
f
2
)
t
+
ϕ
1
−
ϕ
2
)
=
sin
(
2
π
Δ
f
t
+
Δ
ϕ
)
\begin{array}{c}{x_{out}} = \sin (2\pi ({f_1} - {f_2})t + {\phi _1} - {\phi _2})\\ = \sin (2\pi \Delta ft + \Delta \phi )\end{array}
xout=sin(2π(f1−f2)t+ϕ1−ϕ2)=sin(2πΔft+Δϕ)
对于单个静止目标,RX和TX脉冲 之间的时间差是固定为
τ
τ
τ。因此,频率差也是固定的,也就是说IF是一个频率恒定的单音信号。IF的
Δ
f
\Delta f
Δf
Δ
ϕ
\Delta \phi
Δϕ用以估计速度和距离。
2.3 单目标距离估计
PS:此处估计为了简要分析,雷达与目标的相对速度为0.

RX和TX之间的时间差为
τ
=
2
r
c
\tau = \frac{{2r}}{c}
τ=c2r,
r
r
r为距离,
c
c
c为光速。由此可以推出
τ
=
2
r
c
⇒
r
=
Δ
f
⋅
c
2
S
\tau = \frac{{2r}}{c} \Rightarrow r = \frac{{\Delta f \cdot c}}{{2S}}
τ=c2r⇒r=2SΔf⋅c
从上式可以看出,最大探测距离
r
r
r受限于
Δ
f
\Delta f
Δf的最大值,
Δ
f
\Delta f
Δf受限于以下两个因素:
- 带宽 B B B: Δ f < B \Delta f<B Δf<B,因此 r < B ⋅ c 2 S r < \frac{{B \cdot c}}{{2S}} r<2SB⋅c
- IF信号的采样频率 F S F_S FS: F S > 2 Δ f F_S>2\Delta f FS>2Δf 假设一个chirp内的采样频率为 N N N, F S = N / T c F_S=N/T_c FS=N/Tc,可得 r < F S ⋅ c 4 S = N ⋅ c 4 T c S = N ⋅ c 4 B r < \frac{{{F_S} \cdot c}}{{4S}} = \frac{{N \cdot c}}{{4{T_c}S}} = \frac{{N \cdot c}}{{4B}} r<4SFS⋅c=4TcSN⋅c=4BN⋅c
最大探测距离主要受限于
F
s
F_s
Fs,并且与
B
B
B成反比
2.4 多目标距离估计
- 来自三个目标的RX接收信号,每个信号有不同的延时,延时和与目标的距离成正比。
- 不同的RX接收信号转化为多个单音信号,每个信号的频率差是恒定的( f b 1 , f b 2 , f b 3 ) f_{b1},f_{b2},f_{b3}) fb1,fb2,fb3)
- 混频器输出的是多个单音信号的叠加。对该信号进行FFT操作,会产生一个具有不同的峰值的频谱,每个峰值表示在特定距离处的目标。
距离分辨率是指雷达能区分两个不同目标的最小距离。傅里叶变换理论指出:观测时间窗口T,可以分辨间隔超过
1
/
T
1/T
1/T Hz的频率分量。因此,两个目标反射信号频率差的差值需要满足
∣
Δ
f
1
−
Δ
f
2
∣
>
1
T
c
\left| {\Delta {f_1} - \Delta {f_2}} \right| > \frac{1}{{{T_c}}}
∣Δf1−Δf2∣>Tc1根据测距公式:
∣
Δ
f
1
−
Δ
f
2
∣
=
2
S
Δ
r
c
\left| {\Delta {f_1} - \Delta {f_2}} \right| = \frac{{2S\Delta r}}{c}
∣Δf1−Δf2∣=c2SΔr可以得到最小分辨距离
Δ
r
>
c
2
S
T
c
=
c
2
B
\Delta r > \frac{c}{{2S{T_c}}} = \frac{c}{{2B}}
Δr>2STcc=2Bc因此,从式子中我们可以得到提高分辨率的方法:提高带宽
B
B
B,延长chirp信号。
2.5 单目标速度估计
FMCW雷达会发射两个间隔
T
c
T_c
Tc的线性调频脉冲(两个Chirp) ,相应的IF信号为:
在这里有两个近似条件:
- 在一个chirp时间( T c = 40 μ s {T_c} = 40\mu s Tc=40μs)内,目标的移动距离可以近似看成不变。
- TX与RX的频率基本不变: Δ f 1 ≈ Δ f 2 \Delta {f_1} \approx \Delta {f_2} Δf1≈Δf2
相位计算公式:
Δ
ϕ
=
2
π
f
τ
=
2
π
c
τ
λ
=
4
π
r
λ
\Delta \phi = 2\pi f\tau = \frac{{2\pi c\tau }}{\lambda } = \frac{{4\pi r}}{\lambda }
Δϕ=2πfτ=λ2πcτ=λ4πr其中,
f
f
f是发射信号频率,
τ
τ
τ是时间延迟,
λ
λ
λ是发射信号波长,
r
r
r是目标距离。
相位变化为
Δ
ϕ
1
−
Δ
ϕ
2
=
4
π
(
r
1
−
r
2
)
λ
=
4
π
v
T
c
λ
\Delta {\phi _1} - \Delta {\phi _2} = \frac{{4\pi ({r_1} - {r_2})}}{\lambda } = \frac{{4\pi v{T_c}}}{\lambda }
Δϕ1−Δϕ2=λ4π(r1−r2)=λ4πvTc用
λ
=
4
×
1
0
−
3
,
v
=
10
m
/
s
\lambda = 4 \times {10^{ - 3}},v=10m/s
λ=4×10−3,v=10m/s估算,得到相位变化为
0.4
π
0.4\pi
0.4π,较大。
因此得到速度的估计公式:
v
=
(
Δ
ϕ
1
−
Δ
ϕ
2
)
λ
4
π
T
c
v = \frac{{(\Delta {\phi _1} - \Delta {\phi _2})\lambda }}{{4\pi {T_c}}}
v=4πTc(Δϕ1−Δϕ2)λ限制
∣
Δ
ϕ
1
−
Δ
ϕ
2
∣
<
π
{\left| {\Delta {\phi _1} - \Delta {\phi _2}} \right| < \pi }
∣Δϕ1−Δϕ2∣<π时有效,则得到
v
<
λ
4
T
c
v < \frac{\lambda }{{4{T_c}}}
v<4Tcλ

2.6 多目标速度估计
发射一组M个等间隔线性调频脉冲(M个Chirp),
对N这个维度进行FFT处理(距离FFT) ,得到M个频谱。
- 如果目标距离相同,速度不同,M个频谱的峰值相同,但相位不同,包含来自多个目标的相位成分。
- 如果目标距离不同,速度不同,M个频谱都会出现多个峰值,每个峰值的相位都不同。
对M这个维度进行FFT处理(速度FFT) ,可以分离多个相位分量。
速度分辨率:雷达能区分两个不同目标的最小速度差。
傅里叶变换理论指出:两个离散频率
ω
1
\omega_1
ω1和
ω
2
\omega_2
ω2在满足
∇
ω
=
ω
1
−
ω
2
>
2
π
/
M
\nabla \omega = {\omega _1} - {\omega _2} > 2\pi /M
∇ω=ω1−ω2>2π/M时,是可以分辨的。
∇
ϕ
1
−
∇
ϕ
2
=
4
π
T
c
λ
(
v
1
−
v
2
)
>
2
π
/
M
\nabla {\phi _1} - \nabla {\phi _2} = \frac{{4\pi {T_c}}}{\lambda }({v_1} - {v_2}) > 2\pi /M
∇ϕ1−∇ϕ2=λ4πTc(v1−v2)>2π/M
(
v
1
−
v
2
)
>
λ
2
T
c
M
=
λ
2
T
f
({v_1} - {v_2}) > \frac{\lambda }{{2{T_c}M}} = \frac{\lambda }{{2{T_f}}}
(v1−v2)>2TcMλ=2Tfλ
T
f
T_f
Tf为一帧的时间
提高速度分辨率的方法:提高帧时间,Chirp时 间固定的话等价于增加Chirp个数。

参考文献
[1] Milovanovic Vladimir M… On fundamental operating principles and range-doppler estimation in monolithic frequency-modulated continuous-wave radar sensors[J]. Facta universitatis - series: Electronics and Energetics,2018,31(4).
声明
本人所有文章仅作为自己的学习记录,若有侵权,联系立删。本系列文章主要参考了清华大学、北京理工大学、哈尔滨工业大学、深蓝学院、百度Apollo等相关课程。
版权归原作者 yuan〇 所有, 如有侵权,请联系我们删除。