人工智能-常见模型评估(基于sklearn实现)

一、模型评估概述

模型评估的作用

模型评估是模型开发过程不可或缺的一部分。它有助于发现表达数据的最佳模型和所选模型将来工作的性能如何。

按照数据集的目标值不同，可以把模型评估分为分类模型评估和回归模型评估。

模型评估的表现效果

表现效果可以分成两类：过拟合、欠拟合

过拟合(over-fitting)：所建的机器学习模型或者是深度学习模型在训练样本中表现得过于优越，导致在测试数据集中表现不佳

欠拟合(under-fitting)：模型学习的太过粗糙，连训练集中的样本数据特征关系都没有学出来

调优思路：

过拟合的基本调优思路是增加数据量，降低模型复杂度。

欠拟合的基本调优思路是提高特征数量和质量，增加模型复杂度。

二、回归模型评估方法

平均绝对误差(MAE)

    平均绝对误差是所有单个观测值与算术平均值的偏差的绝对值的平均。与平均误差相比，平均绝对误差由于离差被绝对值化，不会出现正负相抵消的情况，因而，平均绝对误差能更好地反映预测值误差的实际情况。MAE的值越接近0，预测模型的准确性越高。

计算公式：

其中，n是样本数，是真实值，是预测值

基于sklearn实现:

from sklearn.metrics import mean_absolute_error

prediction = [2.443532,5.213567,8.168953]
true_value = [2.431354,5.839245,8.123678]
score = mean_absolute_error(true_value, prediction)

能够得到一个评估值，需要对比才能知道模型优劣。

均方误差(MSE)

计算每一个样本的预测值与真实值之差的平方，然后求和再取平均值，其值越小说明拟合效果越好

计算公式：

其中，是真实值，是预测值

基于sklearn实现:

from sklearn.metrics import mean_squared_error

prediction = [2.443532,5.213567,8.168953]
true_value = [2.431354,5.839245,8.123678]
score = mean_squared_error(true_value, prediction)

均方根误差(RMSE)

    均方根误差也称为**标准误差**，预测值与真值偏差的平方与预测次数比值的平方根。均方根误差是用来衡量预测值同真值之间的偏差。标准误差对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。可用标准误差作为评定这一测量过程精度的标准。

计算公式：

基于sklearn实现：

from sklearn.metrics import mean_squared_error
import math

prediction = [2.443532,5.213567,8.168953]
true_value = [2.431354,5.839245,8.123678]

mse_score = mean_squared_error(true_value, prediction)
rmse_score = math.sqrt(mse_score)

决定系数(R-square)

     R2 Score又称为the coefficient of determination。判断的是预测模型和真实数据的拟合程度，最佳值为1，同时可为负值。

计算公式：

其中，是平均值

基于sklearn实现：

prediction = [2.443532,5.213567,8.168953]
true_value = [2.431354,5.839245,8.123678]

from sklearn.metrics import r2_score
score = r2_score(true_value, prediction)

其它评估指标

相对平方误差（Relative Squared Error，RSE）、相对绝对误差（
Relative Absolute Error，
**RAE) **等等

三、分类模型评估方法

混淆矩阵

在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适⽤于多分类)

行索引是
预测结果，列索引是
真实结果

正例假例正例真正例（TP）伪反例（FN）假例伪正例（FP）真反例（TN）
基于sklean实现：

# 假如有一个模型在测试集上得到的预测结果为：  
y_true = [1, 0, 0, 2, 3, 2] # 实际的类别  
y_pred = [1, 1, 0, 2, 1, 3] # 模型预测的类别  
  # 使用sklearn 模块计算混淆矩阵  
from sklearn.metrics import confusion_matrix  
confusion_mat = confusion_matrix(y_true, y_pred)  

准确率Accuracy

准确率是最常用的分类性能指标，预测正确的数占样本总数的比例，即正确预测的正反例数 /总数或者说是分类模型所有判断正确的结集占总观测值的比重。

                    ​​​​​​​        ​​​​​​​        ​​​​​​​        ![\mathrm{Accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}](https://latex.csdn.net/eq?%5Cmathrm%7BAccuracy%7D%3D%5Cfrac%7B%5Cmathrm%7BTP%7D+%5Cmathrm%7BTN%7D%7D%7B%5Cmathrm%7BTP%7D+%5Cmathrm%7BTN%7D+%5Cmathrm%7BFP%7D+%5Cmathrm%7BFN%7D%7D)

基于sklearn实现

from sklearn.metrics import accuracy_score
y_pred = [0,2,1,3,9,7,4]
y_true = [0,1,2,3,2,6,4]

accuracy_score(y_true,y_pred)

精确率Precision

精确率容易和准确率被混为一谈。

正确预测的正例数 /预测正例总数

Precision = TP/(TP+FP)

表现为预测出是正的里面有多少真正是正的。可理解为查准率。

基于sklearn实现在目录F1-score部分

召回率recall

正确预测的正例数 /实际正例总数

与真正率相等，可理解为查全率。正确预测为正占全部正校本的比例

Recall = TP/(TP+FN)

基于sklearn实现在目录F1-score部分

** F1-score**

主要用于评估模型的稳健性，F值是精确率和召回率的调和值，更接近于两个数较小的那个，所以精确率和召回率接近时，F值最大。

F1-Score是综合考虑使用召回率和查准率的指标，F1-Score越高，模型分类效果越好。

计算公式：

其中，P代表Precision，R代表Recall

基于sklearn实现：

from sklearn.metrics import classification_report

y_true = [1, 0, 2, 2, 1]
y_pred = [1, 0, 2, 2, 0]
target_names = ['标签 0', '标签 1', '标签 2']
print(classification_report(y_true, y_pred, target_names=target_names))

结果展示：

                  precision    recall  f1-score   support

        标签 0       0.50      1.00      0.67         1
        标签 1       1.00      0.50      0.67         2
        标签 2       1.00      1.00      1.00         2

      accuracy                           0.80         5
     macro avg       0.83      0.83      0.78         5
  weighted avg       0.90      0.80      0.80         5

ROC曲线与AUC指标

TPR = TP / (TP + FN)

所有真实类别为1的样本中，预测类别为1的比例

FPR = FP / (FP + TN) = 1 - TNR

所有真实类别为0的样本中，预测类别为1的比例

ROC曲线

ROC曲线的横轴就是FPR，纵轴就是TPR，当二者相等时，表示的意义则是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的，此时AUC为0.5。

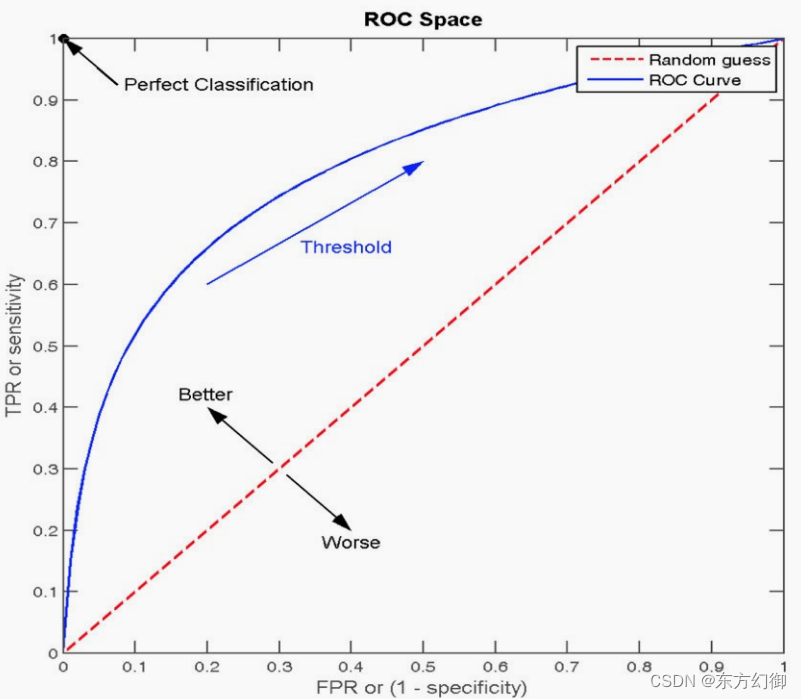
真正的理想情况，TPR应接近1，FPR接近0，即图中的（0,1）点。ROC曲线越靠拢（0,1）点，越偏离45度对角线越好****。

AUC指标

AUC（Area Under Curve）被定义为ROC曲线下的面积(ROC的积分)，通常大于0.5小于1。随机挑选一个正样本以及一个负样本，分类器判定正样本的值高于负样本的概率就是 AUC 值。AUC值(面积)越大的分类器，性能越好

AUC的概率意义是随机取⼀对正负样本，正样本得分⼤于负样本得分的概率

AUC的范围在[0, 1]之间，并且越接近1越好，越接近0.5属于乱猜

AUC=1，完美分类器，采⽤这个预测模型时，不管设定什么阈值都能得出完美预测。绝⼤多数预测的场合，不存在完美分类器。

0.5<AUC<1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

基于sklearn方式实现

import numpy as np
from sklearn.metrics import roc_auc_score

# 构造数据集
y_true = [1, 0, 0, 2, 3, 2] # 实际的类别  
y_pred = [1, 1, 0, 2, 1, 3] # 模型预测的类别  

# 将列表转换为numpy数组
y_true = np.array(y_true)
y_pred = np.array(y_pred)

# 将实际类别中大于等于2的值转换为1
y_true=np.where(y_true>=2,1,0) 
print("AUC值为",roc_auc_score(y_true,y_pred))

需要注意的是，y_true是每个样本的真实类别，必须是0（反例），1（正例）标记

AUC只能⽤来评价⼆分类

AUC⾮常适合评价样本不平衡中的分类器性能

交叉验证

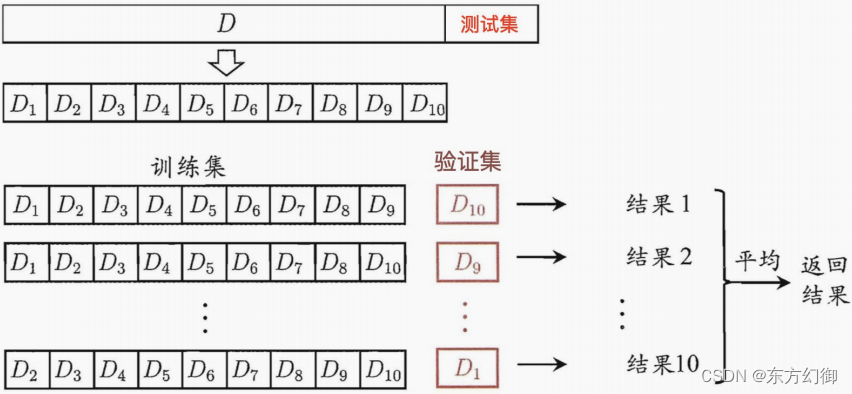
    交叉验证：将拿到的训练数据，分为训练和验证集，既适用于分类模型的评估，也适用于回归模型的评估 

。将数据分成4份，其中⼀份作为验证集。然后经过4次(组)的测试，每次都更换不同的验证集。即得到4组模型的结果，取平均值作为最终结果。称4折交叉验证。

●训练集：训练集+验证集 


●测试集：测试集 

交叉验证API： 

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
    对估计器的指定参数值进⾏详尽搜索
    estimator：估计器对象
    param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
    cv：指定⼏折交叉验证
    fit：输⼊训练数据
    score：准确率

结果分析：
    bestscore__:在交叉验证中验证的最好结果
    bestestimator：最好的参数模型
    cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

基于sklean实现交叉验证： 

# 1、获取数据集
#Iris数据集是常⽤的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是⼀类多重变量分析的数据集。
iris = load_iris()

# 2、数据基本处理 -- 划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

# 3、特征⼯程：标准化
# 实例化⼀个转换器类
transfer = StandardScaler()
# 调⽤fit_transform
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4、KNN预估器流程
# 4.1 实例化预估器类
estimator = KNeighborsClassifier()
# 4.2 模型选择与调优——⽹格搜索和交叉验证
# 准备要调的超参数
param_dict = {"n_neighbors": [1, 3, 5]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
# 4.3 fit数据进⾏训练
estimator.fit(x_train, y_train)

# 5、评估模型效果
# ⽅法a：⽐对预测结果和真实值
y_predict = estimator.predict(x_test)
print("⽐对预测结果和真实值：\n", y_predict == y_test)
# ⽅法b：直接计算准确率
score = estimator.score(x_test, y_test)
print("直接计算准确率：\n", score)

print("在交叉验证中验证的最好结果：\n", estimator.best_score_)
print("最好的参数模型：\n", estimator.best_estimator_)
print("每次交叉验证后的准确率结果：\n", estimator.cv_results_)

结果展示：

⽐对预测结果和真实值：
[ True True True True True True True False True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True]

直接计算准确率：
0.947368421053

在交叉验证中验证的最好结果：
0.973214285714

最好的参数模型：
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')

每次交叉验证后的准确率结果：
{'mean_fit_time': array([ 0.00114751, 0.00027037, 0.00024462]), 'std_fit_time': array([ 1.13901511e-03, 1
.25300249e-05, 1.11011951e-05]), 'mean_score_time': array([ 0.00085751, 0.00048693, 0.00045625]), 'std_scor
e_time': array([ 3.52785082e-04, 2.87650037e-05, 5.29673344e-06]), 'param_n_neighbors': masked_array(data
= [1 3 5],
mask = [False False False],
fill_value = ?)
, 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}], 'split0_test_score': array([ 0.973684
21, 0.97368421, 0.97368421]), 'split1_test_score': array([ 0.97297297, 0.97297297, 0.97297297]), 'split2_te
st_score': array([ 0.94594595, 0.89189189, 0.97297297]), 'mean_test_score': array([ 0.96428571, 0.94642857,
0.97321429]), 'std_test_score': array([ 0.01288472, 0.03830641, 0.00033675]), 'rank_test_score': array([2, 3
, 1], dtype=int32), 'split0_train_score': array([ 1. , 0.95945946, 0.97297297]), 'split1_train_score':
array([ 1. , 0.96 , 0.97333333]), 'split2_train_score': array([ 1. , 0.96, 0.96]), 'mean_trai
n_score': array([ 1. , 0.95981982, 0.96876877]), 'std_train_score': array([ 0. , 0.00025481,
0.0062022 ])}

留出法(hold-out)

    与交叉验证相似，都是常用的评估方法，可以帮助评估模型的性能和泛化能力。直接将数据集D划分为两个互斥的集合，其中⼀个集合作为训练集S，另⼀个作为测试集T。在S上训练出模型后，⽤T来评估其测试误差，作为对泛化误差的估计。

  
       需**注意**的是，训练/测试集的划分要尽可能保持数据分布的⼀致性，避免因数据划分过程引⼊额外的偏差⽽对最终结果产⽣影响，⼀般要采⽤若⼲次随机划分、重复进⾏实验评估后取平均值作为留出法的评估结果。  


基于sklean实现留出法： 

from sklearn.model_selection import train_test_split
#使⽤train_test_split划分训练集和测试集
train_X , test_X, train_Y ,test_Y = train_test_split(
X, Y, test_size=0.2,random_state=0)

留一法

在留出法中，有⼀个特例，叫：留⼀法( Leave-One-Out，简称LOO****），即每次抽取⼀个样本做为测试集。 留⼀法不受随机样本划分⽅式的影响，因为m个样本只有唯⼀的⽅式划分为m个⼦集⼀每个⼦集包含个样本；

from sklearn.model_selection import LeaveOneOut
data = [1, 2, 3, 4]
loo = LeaveOneOut()
for train, test in loo.split(data):
print("%s %s" % (train, test))
'''结果
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]
'''

留⼀法优缺点：

优点：

留⼀法使⽤的训练集与初始数据集相⽐只少了⼀个样本，这就使得在绝⼤多数情况下，留⼀法中被实际评估的模型与期望评估的⽤数据集训练出的模型很相似。因此，留⼀法的评估结果往往被认为⽐较准确。

缺点：

留⼀法也有其缺陷:在数据集⽐较⼤时，训练m个模型的计算开销可能是难以忍受的。