MATLAB小提琴仿真与代码实现（数学物理方程）大作业

1. 问题背景与介绍

振动是自然界最普遍的现象之一，也是所有物体发声的来源，可以说振动与我们的

生活息息相关。一直以来，科研人员在振动领域投入了大量研究，对振动过程和机理的

认识也日益深化，使振动能够趋利避害。振动力学是关于机械振动的一门重要学科，它

为合理解决工程中遇到的各种振动问题提供了理论依据，本问主要内容就是借助振动力学来研究弦振动方程去探究小提琴琴弦的振动特性，以及与之密切相关影响的其它因素，通过MATALB仿真进行实现。

基础乐理知识介绍

标准音：目前国际通用的标准高度是每秒钟振动 440 次的 a 音，即以小字一组的 a 为 “标准音”。乐音体系中的各音级，其高度都有一定的标准。

八度就是指音程关系。在音乐中，相邻的音组中相同音名的两个音，包括变化音级，称之为八度。

十二平均律：将一个纯八度（如 c1-c2）分成十二个均等的部分。

用十二平均律构成的七声音阶如表1.1：

1. 任务要求

已知小提琴的钢质E弦(小提琴最细的弦) ，其空弦基频为660Hz。试根据细弦横向振动的知识和结论，完成下列任务的仿真程序。（分析过程中，只考虑弦的横向振动。）

从以下几个方面进行分析，并通过MATlab进行仿真和验证。

1、小提琴的高八度A音(2×440Hz)时，弦长是多少，拉力多大?

2、小提琴的音准受哪些因素影响，各因素影响的大小分别是多少（用相对误差关系来表示）?

3、用MATLab仿真其发音，检验自己在发生多大的设计误差时能听得出来。

4、在程序设计中，时间序列取值间隔应注意哪些问题，为什么?

1. 设计原理

弦振动方程的确立与求解

首先，我们来分析一根琴弦的振动。一根均匀柔软的弦受到一个垂直于弦方向的扰动以后开始作小振幅的振动，取绷紧弦的位置为平衡位置， 振动的方向垂直于弦的平衡 位置，这样的振动称为横振动。 假设弦的平衡位置为 x 轴，取振动中的一段弦元 AB，设弦的线密度是p,两端受到的张力为 T，作用在单位质量上的外力是 f(x,t)，方向沿着 y 轴，弦的初始位移和初始速度分别用 φ(x)和表示，弦元偏离平衡位置的距离是 。

演奏小提琴比较常见的一种技法是拨弦[1]。 拨弦把琴弦拨离平衡位置，使其振动发声。 这相当于在x处把弦拉高到高度h，然后松开，使其自由振动，即弦振动的初始位移不为零而初速度为零。

由数学物理知识可得，小提琴可转化为物理实际问题弦振动问题的定解问题。可以列出下列方程组：

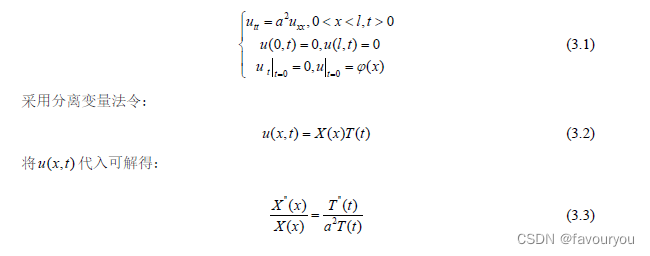
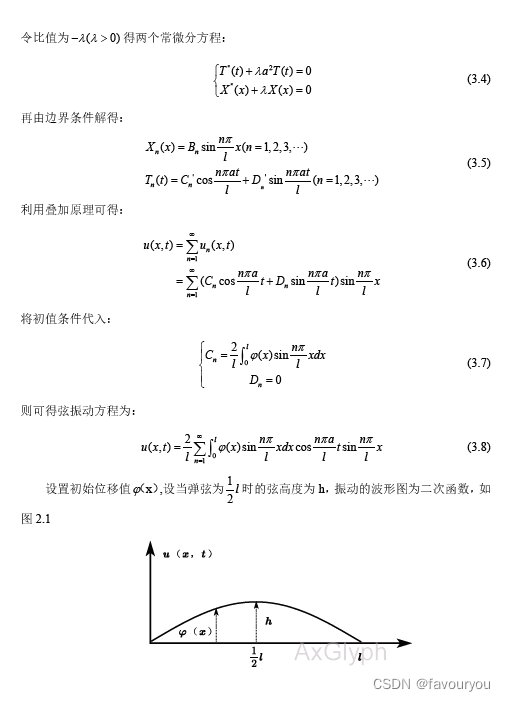
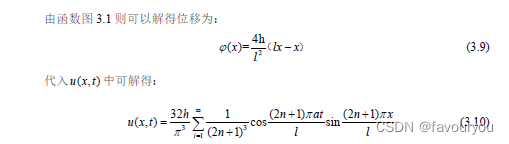
本文只考虑了初值条件为无初速度有初位移的情况，在真实的复杂情况可能初值不一样，结果可能造成了误差。

小提琴振动发音原理

在研究小提琴的振动之前，有必要了解一下小提琴的发音原理。小提琴就是靠演奏者施加拉力，这个力通过弓作用在琴弦上，使琴弦产生振动，弦的振动施加力给琴码，琴码通过两只码脚把琴弦的横向力转变为驱动力，施加给面板，而背板和面板通过音柱相连接，这样面板和背板都产生振动，从而使小提琴琴身产生振动发出声音，声音又通过空气传给人耳。

小提琴的发音：取决它的木质和相应的结构,取决于木材的振动频率和它对弦振动的反应,优质的小提琴能将每个音符的基音和泛音都同样灵敏地传播出去。本文只研究琴弦的横振动,所以发音效果会有一定的误差。

**横振动[2]**（transverse vibration）。将弦挑离其平衡位置再放掉，弦就开始作一个扁

纱锭型的振动，它的振幅限制在两条明确的曲线之内。弦的横振动频率，可以用泰勒公式来表达，即

式中 f 为弦的振动频率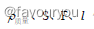，依次为弦的密度、截面积、张力和长度。且可

以看出横振动频率与弦长成反比，与张力的平方根成正比，与弦的密度、截面积的平方

根成反比。

为了方便计算且与前面弦振动方程传播系数a2量纲保持一致，故采取，这里的是弦的线密度即：

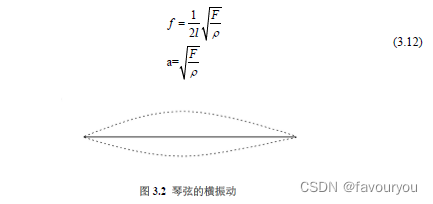
琴弦的横振动只考虑当小提琴水平放，琴弦上下来回振动如图3.2所示。

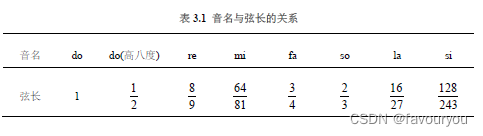
由频率公式可以得出频率与弦长之间的关系，进而得出与七声音阶之间的关系，如表2.1

琴弦材料参数确定

通过查询琴弦生产公司PIRASTRO官网，我们选择如表2.2的E（小提琴最细的琴弦）琴弦材料参数。

在此我们定弦长L=328mm=0.328m（注：此处我们选用的是4/4M尺寸的小提琴，即成人常用小提琴）

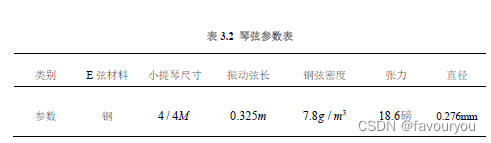
弦的密度为,E弦直径为0.276mm则半径为0.138mm=0.000138m,由公式线密度=密度x琴弦的横截面积得，E弦的线密度是。

对张力F进行调整，利用泰勒公式已知空弦时基频为660Hz，利用振动弦长，弦密度可解得拉力F=86N。

至此小提琴参数确定为：

1. 问题求解

问题一

提琴的高八度A音(2×440Hz)时，弦长是多少，拉力多大?

由前面介绍的乐理知识，可知当小提琴发A音即对应为la，高八度时频率为2x440hz

此时利用前面泰勒定理公式（3.12）

                                                     ![](https://img-blog.csdnimg.cn/2f219874bdc44a5e9c61482727dc8f8a.png)                                

   则第一问已解。

问题二

小提琴的音准受哪些因素影响，各因素影响的大小分别是多少（用相对误差关系来表示）?

音准是由频率决定的所以理论上讲音准受弦长、拉力与线密度影响。

即问题二解出各因素对音准的影响关系得解。

问题三

用MATLab仿真其发音，检验自己在发生多大的设计误差时能听得出来。

由已知八度音振动发声的频率如表4.1

表4.1 各音节的振动发声频率表

音名

do

re

mi

fa

so

la

si

do(高八度)

频率（Hz）

261.6

293.7

329.6

349.2

392

440

493.9

523.3

基于表4.1，在matlab中进行仿真，对于该题无论你改变哪个量，始终影响这的是频率f的改变，通过改变各音节每次减少或增加的频率数，通过双层循环，每次输出八度音，测试自己的误差，得出下表4.2：

音节

频率界值（Hz）

do

200-275

Re

280-310

mi

315-340

fa

345-370

so

380-420

la

425-460

si

480-510

表4.2 频率误差表

则。

问题四

在程序设计中，时间序列取值间隔应注意哪些问题，为什么?

我们对弦振动方程进行matlab仿真模拟，基于现实中小提琴琴弦振动的情况，从最开始振动位移很大，到慢慢衰减到最后一直位移为0才停止下来，我们选择小提琴E弦为基础在matlab中进行仿真，画出对比图4.1：

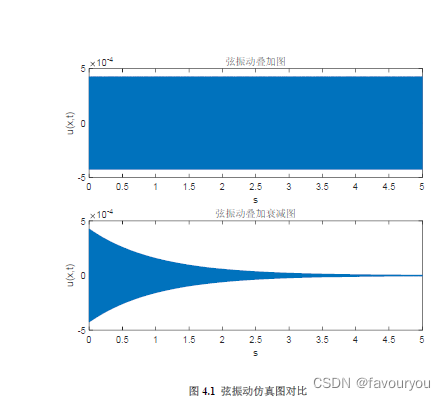
图4.1 弦振动仿真图对比

图4.1中下图才是真正现实振动波形图

所以对于时间序列的取值，倘若时间序列太长，则振动时间会加长，无衰减的情况下，琴弦发出的声音会一直保持，声音与现实有点差距，所以为了更加真实的模拟现实小提琴的声音，选择稍微短点的时间序列或者在发声函数上加一个衰减函数来达到现实中的弦振动，但时间序列的取值也不能太短，为人耳可听频率为20Hz-20KHz，因此，经试验时间长度必须大于等于0.002秒才可以听出不同声音。

至于采样频率，它当然越高越好，因为离散点越密集越像连续图像真实性越高，当然那样运算量也越大，经测验5kHz的采样率仅能达到人们讲话的声音质量。11kHz的采样率是播放小段声音的最低标准，是CD音质的四分之一。22kHz采样率的声音可以达到CD音质的一半，目前大多数网站都选用这样的采样率。

1. 总结

本文基于对小提琴发声的背景下，对琴弦振动进行了深入分析，从振动力学角度入手，给出了在横振动的情况下，建立了弦振动方程并进行了求解，选择合适的小提琴E琴弦，并在matlab中进行了仿真，仿真出了真实音效八度音节和振动位移图，同时也进行也来误差分析，从仿真图的结果上体现加上衰减函数的发声函数与现实琴弦振动更加贴合。

综上所述，所得结果较好的体现了现实真实琴弦振动的情况，但仿真数据的误差与现实仍有差距。

参考文献

[1]李韵,郭怡文,吕郁文.基于Matlab环境的弦振动方程的图像与音效模拟[J].科协论坛(下半月),2009(07):74-75.

[2]贾雄. 小提琴弦振动与琴体腔谐振研究[D].华南理工大学,2013.

[3]张承忠. 小提琴振动机理及声学品质研究[D].华南理工大学,2014.

[4]吕林波. 小提琴音响品质评估与优化[D].上海交通大学,2011.

附录

八度音阶代码（可调）

%循环发声八度音来检测自己的听力误差，通过调整参数检验上限和下限

function qing

fs=100000;                                                %采样频率

shijianxulie=1/fs:1/fs:1;                                %时间序列

fqiduyin_a=[261.6,293.7,329.6,349.2,392,440,493.9,523.3];%八度音节对应的频率

for a=0:1:10                                             %外循环

    fqiduyin_a=fqiduyin_a-5;                             %每次将频率减少的值

        for i=1:1:8                                       %内循环

        fasheng(1,:)=sin(2*pi*shijianxulie*fqiduyin_a(1,i));     %发声函数转化为离散信号

        sound(fasheng.*exp(-shijianxulie),fs);                                 %让振动发声

        delay(2);                                       %延迟时间

        end

end

function delay=delay(n)

tic;                   %启动秒表计时器

for t=0.001:0.001:n    %按秒算

    while toc<t        %当秒表小于时间

    end

end

end

弦振动图

clc

clear;

F=86;                                                              %初始张力                                                         

P_string=4.67e-4;                                                   %钢弦密度                                               

h=0.01;                                                             %弹弦高度

V=(F/P_string)^(0.5);                                               %传播常数

Length_string=0.325;                                                %振动弦长

f=V/(2*Length_string);                                              %频率计算公式

x=0.5*Length_string;                                                %弹琴弦位置

z=0;zn=0;

fs=10000;                                                            %采样频率

t=0:1/fs:5;                                                          %时间序列

for n=1:10                                                           %设置叠加次数

      zn=32*h/pi^3*(1/(2*n+1)^3)*cos((2*n+1)*pi*V/...  

          Length_string*t)*sin((2*n+1)*pi*x/Length_string);         %弦振动方程

       z=z+zn;                                                       %叠加

end

subplot(2,1,1)

plot(t,z);                                                          %画图无衰减

title('弦振动叠加图');xlabel('s');ylabel('u(x,t)');

z=z.*(exp(-1*t));                                                   %乘以指数衰减

subplot(2,1,2)

plot(t,z);                                                          %画图衰减

title('弦振动叠加衰减图');xlabel('s');ylabel('u(x,t)');

音节图加音调逐级递增

clc
clear;
f_tone_0=440;%A调基频
Step_half_scale=2^(1/12);%十二节律
fs=100000;%采样频率
t_tone=1/fs:1/fs:1;%时间序列
for i=1:1:13  %根据乐理知识十二节律与八度音节的关系
    Scale_tone(i)=f_tone_0/(Step_half_scale^(10-i));%每个基本唱名与A的关系式
    if i==1%do时与A的关系
        y_tone(1,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
        x_tone(1)=Scale_tone(i);%do
    else if i==3
            y_tone(2,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
            x_tone(2)=Scale_tone(i);%re
        else if i==5
                y_tone(3,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
                x_tone(3)=Scale_tone(i);%mi
            else if i==6
                    y_tone(4,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
                    x_tone(4)=Scale_tone(i);%fa
                else if i==8
                        y_tone(5,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
                        x_tone(5)=Scale_tone(i);%so
                    else if i==10
                            y_tone(6,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
                            x_tone(6)=Scale_tone(i);%la
                        else if i==12
                                y_tone(7,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
                                x_tone(7)=Scale_tone(i);%si
                            else if i==13
                                    y_tone(8,:)=sin(2*pi*t_tone*Scale_tone(i));%发音函数转化为离散信号
                                    x_tone(8)=Scale_tone(i);%高八度do
                                end
                            end
                        end
                    end
                end
            end
        end
    end
end
figure(1)%创建图窗窗口
hold on;%保留图
xlabel('\bf音节：（cdefgabc）');%x坐标
ylabel('\bf音节音频：（Hz）');%y坐标
title('\bf8度音节音频示意图（A：4400Hz');%图题
x_sub=1:1:8;%离散序列x坐标值
Sub_stem=zeros(1,8);%离散序列
stem(x_sub,Sub_stem);%绘制离散序列图示
xlim([0,8]);%x的刻度
ylim([0,600]);%y的刻度
for i=1:1:8%循环八次
    time_pause=1.2;%时间暂停1.2s
    if i==8%发高八度do时
        time_pause=2.4;%暂停2.4s
    end
    stem(i,x_tone(i),'fill');%绘制离散序列，并创建一个针状图并填充终止每个针状图的圆
    sound(y_tone(i,:),fs);%循环发声
    pause(time_pause);%暂停函数
end
hold off