你程序的复杂性知道嘛？

14天阅读挑战赛
努力是为了不平庸~
算法学习有些时候是枯燥的，这一次，让我们先人一步，趣学算法！

程序的复杂性

• 时间的复杂度
• 空间的复杂度
• 爆炸级增量
• 总结

这是我在力扣网上找的一个题，题目中有这样的限制条件，你知道什么是时间的复杂的吗？你知道该怎样计算时间的复杂度吗?

1.时间的复杂性

好的算法的判断方法是：高效率、低存储。那么计算运行的速度，学习时间的复杂性是十分有必要的。

算法的时间复杂度就是算法运行所需的时间。由于相同配置的计算机进行一次基本运算的时间是一定的，可以用算法基本运算的执行次数来衡量算法的效率，因此我们将算法基本运算的执行次数作为时间复杂度的衡量标准。

  观察算法1-1并分析算法的时间复杂度
  
  //算法1-1
  int sum = 0;//运行1次
  int total = 0;//运行1次
  for (int i = 1; i <= n; i++)//运行n+1次
  {
    sum = sum + i;//运行n次
    for (int j = 1; j <= n; j++)//运行n*(n+1)次
    {
        total = total + i * j;//运行n*n次
    }
  }

把算法1-1中所有语句运行的次数加起来：1+1+n+1+n+n*(n+1)+n*n。这可以用一个函数T(n)来表示：

      T(n)=2n^2+3n+3

当n足够大时，例如n=10^5，T(n)=210^10+310^5+3。可以看出，算法的运行时间主要取决于最高项。其实时间的复杂度也与最高项息息相关，接下来让我们化简求时间的复杂度。
化简得规则为：

• 忽略常数项 //T(n)=2n^2+3n
• 忽略低阶项 //T(n)=2n^2
• 忽略最高阶的系数 //T(n)=n^2

所以f(n)=n^2，时间复杂度的表示为 O(f(n))，
所以则时间复杂度的表示为 O(n^2)

以上就是时间复杂度的求法，让我们来几道题练练手吧：

• 第一题//算法1-2int i = 1; //运行1次while (i <= n) //假设运行x次{ i = i * 2; //假设运行x次}对于算法1-2我们无法立即确定while以及i=i*2语句运行了多少次。这时可假设运行了x次，每次运行后 i的值为2、2^2、...、2^x，当2^x>n结束，此时x>log_2^n，所以while运行的次数为log_2^n+1， i=i\*2运行次数为log_2^n，所以算法1-2的运行次数为1+2log_2^n，时间的复杂度为O(f(n))=O(log_2^n)。

在计算时间复杂度时，可以只考虑对算法运行时间贡献大的语句，而忽略那些运行次数少的语句。循环语句中处在循环内层的语句往往运行次数最多，它们是对运行时间贡献最大的语句。例如，在1-1中，total=total+i*j是对算法贡献最大的语句，只计算该语句的运行次数即可。

不是所有的算法都能直接计算运行次数
例如算法1-3，在数组a[n]中顺序查找x并返回其下标i。如果没有找到，则返回-1。

 //算法1-3
int  findx(int x)
{
        int i = 0;
        for(i = 0; i<n; i++)
        if(a[i] == x)
              return i;
        return -1;
}

对于该算法，很难计算到底执行了多少次，因为运算次数依赖于数组中x的位置。如果第一个元素是x，则执行一次（最好的情况）；如果最后一个是x，则执行x次（最坏的情况）；如果分布概率均等，则平均运行次数为(n+1)/2。
//
有些算法，如排序、查找、插入算法等，可以分为最好、最坏和平均情况分别求算法渐进复杂度。但考察一个算法时通常考查最坏的情况，而不是考察最好的情况，最坏的情况对衡量算法的好坏具有实际意义。

2.空间的复杂度

空间的复杂度：算法占用空间的大小。
算法复杂度的本意是指算法在运行过程中占用了多少存储空间。算法占用的存储空间包括：

• 输入/输出数据
• 算法本身
• 额外需要的辅助空间输入/输出数据占用的空间时必需的，算法本身占用的空间可以通过精简算法来缩减，但缩减的量是很小的，可以忽略不计。算法在运行时所使用的辅助变量占用的空间（即辅助空间）才是衡量算法空间复杂度的关键因素。

我们可以类比时间复杂度，当n趋近于无限大时，常量和低阶项都可以忽略不记。在这里，输入/输出、算法本身可以忽略不记。

请分析算法1-4的空间复杂度

void swap(int* x, int* y)      //交换x，y的值
{
       int temp;
       temp = *x;         //temp为辅助空间
       *x = *y;
       *y = temp;
}

算法1-4使用了辅助空间temp，空间复杂度为O(1)

请分析算法1-5（递归）空间复杂度

int fac(int n){ //计算n的阶乘
      if(n == 0&&n == 1)
           return 1;
      else
           return n*fac(n-1);
}

阶乘是典型的递归调用问题，递归包括递推和回归。递推是将原问题不断分解成子问题，直至满足结束条件，返回最近子问题的解；然后逆向逐一回归，最终到达递推开始的原问题，返回原问题的解。

请计算n=5的空间复杂度。

计算机使用一种称为“栈”的数据结构，“栈”类似于一个放盘子的容器，每次从顶端放进去一个，拿出来的时候只能从顶端拿一个，不允许从中间插入或抽取，因此，称为“先进后出”。

递归算法的空间复杂度需要计算递归使用的栈空间

           5的阶乘进栈的过程

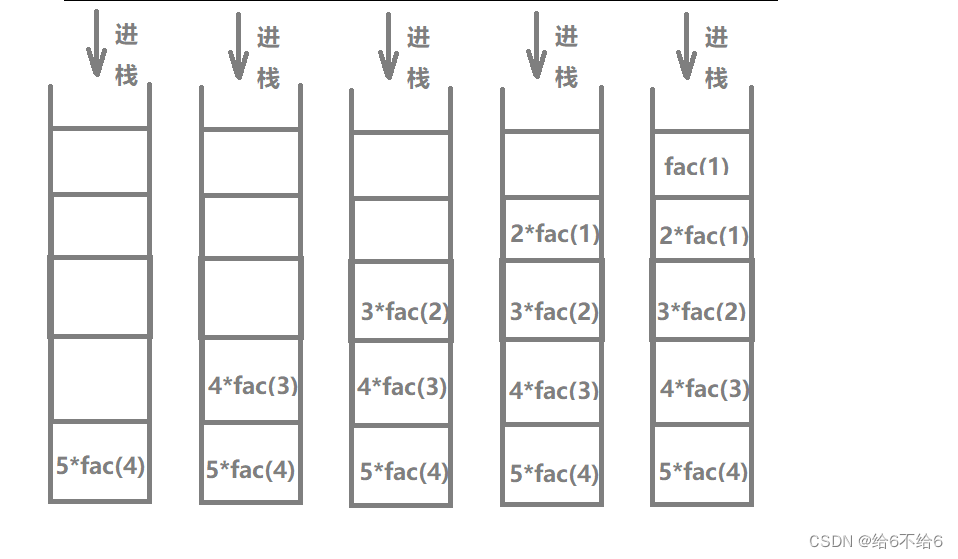
        5的阶乘出栈的过程

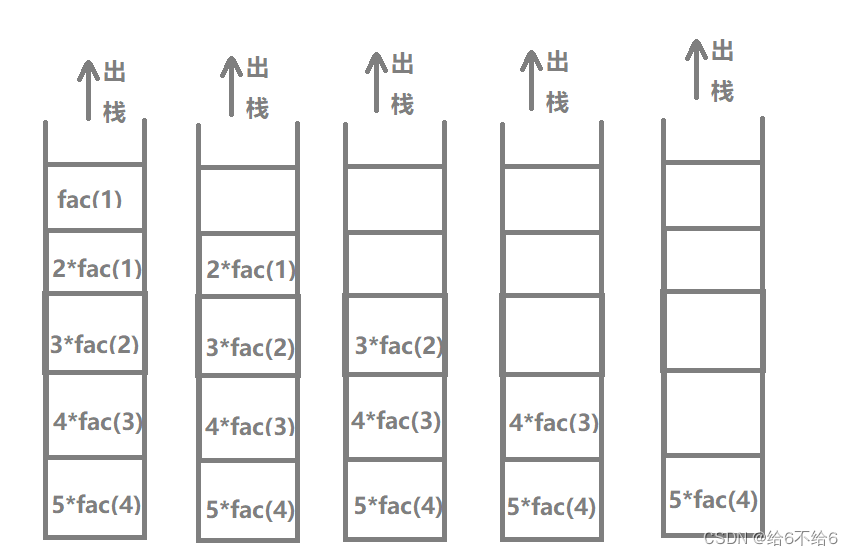
则5的阶乘的辅助空间是5，空间复杂度为5
则n的阶乘的空间复杂度为n

3.爆炸级增量

一盘棋的麦子

有个古老的传说，一位国王的女儿不幸落水，水中有很多鳄鱼，国王情急之下下令：“谁能把公主救上来，就把女儿嫁给他。”很多人纷纷退让，一个勇敢的小伙子挺身而出，冒着生命危险把公主救了上来，国王一看是个穷小子，想要反悔，说：“除了女儿，你要什么都可以。”小伙子说：“好吧，我只要一盘棋的麦子。你再第一个格子里放一粒麦子，第二个格子里放2粒麦子，在第三个格子里，放4粒麦子，在第四个格子，放8粒麦子，以此类推，每一个格子里麦子的粒数都是前一个格子里的麦子粒数的两倍。把这64个格子放满了就行，我就想要这么多。”国王听后哈哈大笑，觉得小伙子的要求很容易满足，满口答应。结果方向，把全国的麦子都拿来，也填不完这64个格子…国王无奈，只好把女儿嫁给了这个小伙子。

我们把这个故事当作数学题，试着用你那聪明的大脑求需要的麦粒数目是多少？

解：
S=1+21+22+23+…+263
S=264-1
一粒麦子的重量大约是41.9毫克，这些麦粒的总重量约等于7729000亿千克
全世界人口按77亿计算，每个人差不多可以分得100 000千克（即100吨）
我们称这样的函数为爆炸增量函数，想一想，如果算法的时间复杂度是O(2n)会怎样？随着n的增长，算法会不会”爆掉“？我们经常见到有些算法调试没问题，运行一段时间也没问题，但在关键的时候宕机（即死机）。例如在我们高考完过后，每个考生在那一天都要查自己的成绩，查成绩的网站就那一个，1000个人查成绩没问题，10000个也没问题，可一旦涉及到几十万几百万的时候网站就容易宕机，登陆不上。

常见的算法复杂度

常见的算法时间复杂度有以下几类。
（1）常数阶。

常数阶算法的运行次数是一个常数，如5、20、100。常数阶算法的时间复杂度通常用O(1)表示。

（2）多项式阶。

很多算法的时间复杂度是多项式，通常用O(n)、O(n^2^)、O(n^3^)等表示。

（3）指数阶。

指数阶算法的运行效率极差，程序员往往像躲“恶魔”一样避开这类算法。指数阶算法的时间复杂度通常用
O(2^n^)、O(n!)、O(n^n^)等表示。

（4）对数阶。

对数阶算法的运行效率较高，通常用O(logn)、O(nlogn)等表示。

指数阶增量随着x的增加而急剧增加，而对数阶增长缓慢。它们之间的关系如下：

O(1)<O(logn)<O(n)<O(nlogn)<O(n^2^)<O(n^3^)<O(n^n^)<O(n!)<O(n^n^)

注意

在设计算法时，我们要注意算法复杂度增量的问题，尽量避免爆炸级增量。

4.一个好的算法的产生过程

题目：斐波那契数列如下：

1，1，2，3，5，8，13，21，34，......求数列前n项和。

算法设计：

算法1-6：递归

intFib1(int n){if(n ==1|| n ==2)return1;elsereturnFib1(n -1)+Fib1(n -2);}

当写完一个算法时，需要考虑如下3个问题。

• 算法是否正确？
• 算法复杂度如何？
• 算法能否改进？

算法1-6经过公式与运行实例，得出该算法的正确性没有问题
计算算法的时间复杂度：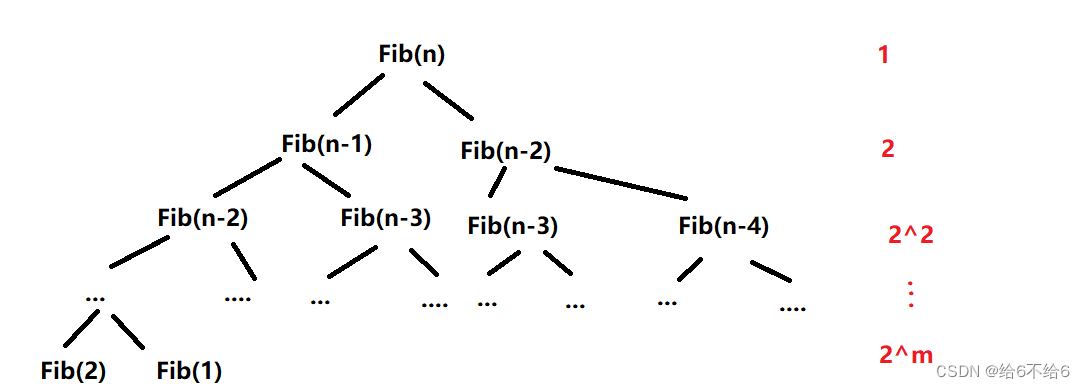

这是一份递归树，每往下递归一行，函数Fib都要分裂为两个Fib函数，每个程序的函数都要进行计算，所以时间复杂度是指数阶的。算法1-6的无论是时间复杂度还是空间复杂度都属于爆炸增量函数，这在算法设计中是应当避开的，那么算法1-6能不能改进呢？

算法1-7

intFib2(int n){int arr[n +1]={0};
    arr[1]=1;
    arr[2]=1;for(int i =3; i <= n; i++){
        arr[i]= arr[i -1]+ arr[i -2];}return arr[n];}

很明显，算法1-7的算法复杂度为O(n)，因为算法1-7仍然遵从F(n)的定义，所以正确性没有问题，但时间复杂度却从算法1-6的指数阶降到了多项式阶，算法效率有了重大突破！使用了一整个数组的辅助变量，算法的空间复杂度为O(n);

算法1-7使用了一整个数组的辅助变量，其实我们仔细观察，我们只需要一个辅助变量即可，请看！

算法1-8

intFib3(int n){if(n ==1|| n ==2)return1;int s1 =1;int s2 =1;int temp =0;for(int i =3; i <= n; i++){
        temp = s1;
        s1 = s2;
        s2 = temp + s2;}return s2;}

很明显，我们只用了一个辅助变量temp即可，空间复杂度降为O(1)，时间复杂度为O(n);

5.总结

• 将程序执行的次数作为时间复杂度的衡量标准
• 时间复杂度通常用符号O(f(n))表示
• 衡量算法的好坏通常考查算法的最坏情况
• 空间复杂度只计算辅助空间
• 递归算法的空间复杂度需要计算递归使用的栈空间
• 设计算法应避免爆炸级增量复杂度