决策树之ID3的matlab实现

森林内的两条分叉路，我选择了人迹罕见的一条，从此一切变得不一样。
------佛洛斯特Robert Frost

目录

一 .决策树介绍

1.1 相关概念

1.2 图形表示

1.3 规则表示

二.决策树的信息计算

三.ID3相关介绍

3.1 ID3算法概述

3.2 算法流程

四.matlab实现

4.1 数据集

4.5 代码实现

一 .决策树介绍

1.1 相关概念

决策树是什么？ 决策树当然顾名思义用来做决策。

怎么决策？ 以树状的形式来表示逻辑的一种决策过程。既然是一棵树，必然有树枝，那么把树枝的分叉表示我们的一种划分，来判断往哪个树枝继续前进。决策树有以下部分组成：

（1）根节点：即为决策树的起点

（2）分支点：属于内部节点，所谓分支就是要选择一个某一个特征或者属性

（3）内部节点：包括根节点和分支点，通常取样本的大部分

（4）叶节点：即为决策树的终点，决定了因变量分类的标签

1.2 图形表示

决策树的图形表示如下:

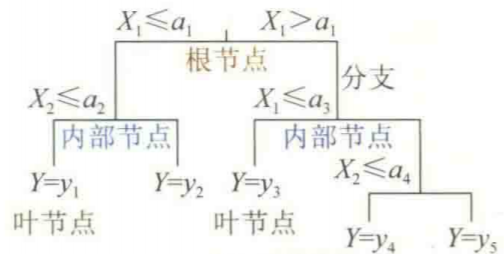
1.3 规则表示

决策树的规则表示为：

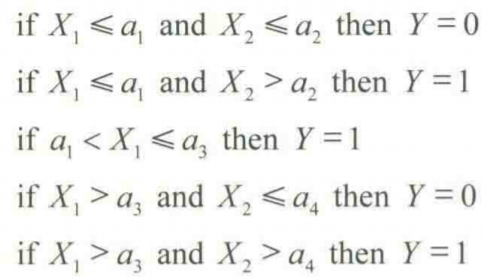
二.决策树的信息计算

为什么我们要做信息计算？这是为了选择决策树的分支，我们为了做分枝，就要计算特征变量的一些信息，来选择信息增益最大的特征变量，从而作为决策树的分枝。

怎么做信息计算？首先介绍如下概念：

（1）熵：由于要做分枝，熵相当于分枝的乱度，分枝是要找降低乱度多的，信息增益大的。例如我们要扔一枚硬币，正反两面出现的概率都为1/2，此时若有人说硬币一定会是正面，那么此时熵就为0，即乱度为0，计算公式如下：

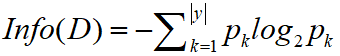
系统越有序，信息熵就越低；反之，一个系统越乱，信息熵就越高。所以，信息熵可以说是系统有序化程度的一个衡量。

（2）信息增益：就是信息产生的价值，例如上述硬币的例子，信息增益=1-0=1，计算公式如下：

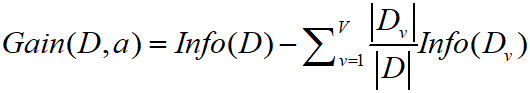
信息增益是针对具体的属性来讲的，选择一个属性来划分数据集D，分别计算划分后两个集合的纯度，然后，把这两个集合的熵求加权平均，跟之前没有划分的时候的熵相比较，用后者减去前者，得到的就是该属性对样本集D划分所得到的信息增益。

三.ID3相关介绍

3.1 ID3算法概述

ID3为迭代二叉树3代，ID3算法实际上是一种贪心算法，用来构造决策树。ID3算法起源于概念学习系统（CLS），在每一个节点还尚未被用来划分具有最高信息增益的特征来作为划分标准，然后继续这个过程，直到决策树能完美的完成分类训练到样例。

3.2 算法流程

输入：样本集合S，属性集合A

输出：ID3决策树。

（1)若所有种类的属性都处理完毕，返回；否则执行2）

（2)计算出信息增益最大属性a，把该属性作为一个节点。如果仅凭属性a就可以对样本分类，则返回；否则执行3）

（3)对属性a的每个可能的取值v，执行一下操作：

i. 将所有属性a的值是v的样本作为S的一个子集Sv；

ii. 生成属性集合AT=A-{a};

iii.以样本集合Sv和属性集合AT为输入，递归执行ID3算法；

四.matlab实现

4.1 数据集

数据集选取UCI数据集里边的mushroom数据，样式如下：

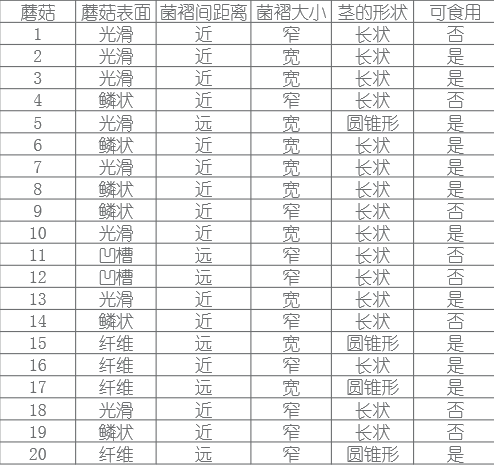
数据集下载地址：https://archive.ics.uci.edu/ml/datasets/Mushroom

mushroom数据

4.5 代码实现

%样本集的熵
sum=20;yes=12;no=8;
Entropy_S=-(yes/sum)*log2(yes/sum)-(no/sum)*log2(no/sum);
%disp(['样本集S的熵：',num2str(Entropy_S)])
%蘑菇表面状况
sum_s=8;yes=6;no=2;%蘑菇表面光滑
Entropy_s=-(yes/sum_s)*log2(yes/sum_s)-(no/sum_s)*log2(no/sum_s);
%disp(['蘑菇表面光滑的熵：',num2str(Entropy_s)])
sum_y=6;yes=2;no=4;%蘑菇表面鳞状
Entropy_y=-(yes/sum_y)*log2(yes/sum_y)-(no/sum_y)*log2(no/sum_y);
%disp(['蘑菇表面鳞状的熵：',num2str(Entropy_y)])
sum_g=2;yes=0;no=2;%蘑菇表面凹槽
Entropy_g=-0-(no/sum_g)*log2(no/sum_g);
%disp(['蘑菇表面鳞状的凹槽：',num2str(Entropy_g)])
sum_f=4;yes=4;no=0;%蘑菇表面纤维
Entropy_f=-(yes/sum_f)*log2(yes/sum_f)-0;
%disp(['蘑菇表面纤维的熵：',num2str(Entropy_f)])
Gain_surface=Entropy_S-(sum_s/sum)*Entropy_s-(sum_y/sum)*Entropy_y-(sum_g/sum)*Entropy_g-(sum_f/sum)*Entropy_f;
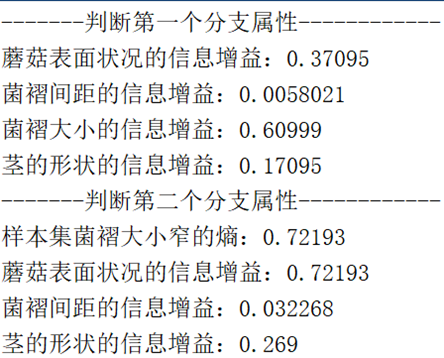
disp(['蘑菇表面状况的信息增益：',num2str(Gain_surface)])
%菌褶间距
sum_d=6;yes=4;no=2;%菌褶间距远
Entropy_d=-(yes/sum_d)*log2(yes/sum_d)-(no/sum_d)*log2(no/sum_d);
sum_c=14;yes=8;no=6;%菌褶间距近
Entropy_c=-(yes/sum_c)*log2(yes/sum_c)-(no/sum_c)*log2(no/sum_c);
Gain_gillsize=Entropy_S-(sum_d/sum)*Entropy_d-(sum_c/sum)*Entropy_c;
disp(['菌褶间距的信息增益：',num2str(Gain_gillsize)])
%菌褶大小
sum_b=10;yes=10;no=0;%
Entropy_b=-(yes/sum_b)*log2(yes/sum_b)-0;
sum_n=10;yes=2;no=8;%
Entropy_n=-(yes/sum_n)*log2(yes/sum_n)-(no/sum_n)*log2(no/sum_n);
Gain_gillsize=Entropy_S-(sum_b/sum)*Entropy_b-(sum_n/sum)*Entropy_n;
disp(['菌褶大小的信息增益：',num2str(Gain_gillsize)])
%茎的形状
sum_t=4;yes=4;no=0;%
Entropy_t=-(yes/sum_t)*log2(yes/sum_t)-0;
sum_e=16;yes=8;no=8;%
Entropy_e=-(yes/sum_e)*log2(yes/sum_e)-(no/sum_e)*log2(no/sum_e);
Gain_gillsize=Entropy_S-(sum_t/sum)*Entropy_t-(sum_e/sum)*Entropy_e;
disp(['茎的形状的信息增益：',num2str(Gain_gillsize)])

disp('-------判断第二个分支属性------------')
%% 判断第二个分支属性
%在分类时，分支属性菌褶代大小为宽时，蘑菇均为可食用，所以以菌褶大小窄继续划分
%样本集菌褶大小窄的信息熵
sum=10;yes=2;no=8;
Entropy_S=-(yes/sum)*log2(yes/sum)-(no/sum)*log2(no/sum);
disp(['样本集菌褶大小窄的熵：',num2str(Entropy_S)])
%蘑菇表面状况
sum_s=2;yes=0;no=2;%蘑菇表面光滑
Entropy_s=0-(no/sum_s)*log2(no/sum_s);
sum_y=4;yes=0;no=4;%蘑菇表面鳞状
Entropy_y=0-(no/sum_y)*log2(no/sum_y);
sum_g=2;yes=0;no=2;%蘑菇表面凹槽
Entropy_g=0-(no/sum_g)*log2(no/sum_g);
sum_f=2;yes=2;no=0;%蘑菇表面纤维
Entropy_f=-(yes/sum_f)*log2(yes/sum_f)-0;
Gain_surface=Entropy_S-(sum_s/sum)*Entropy_s-(sum_y/sum)*Entropy_y-(sum_g/sum)*Entropy_g-(sum_f/sum)*Entropy_f;
disp(['蘑菇表面状况的信息增益：',num2str(Gain_surface)])

%菌褶间距
sum_d=3;yes=1;no=2;%菌褶间距远
Entropy_d=-(yes/sum_d)*log2(yes/sum_d)-(no/sum_d)*log2(no/sum_d);
sum_c=7;yes=1;no=6;%菌褶间距近
Entropy_c=-(yes/sum_c)*log2(yes/sum_c)-(no/sum_c)*log2(no/sum_c);
Gain_gillsize=Entropy_S-(sum_d/sum)*Entropy_d-(sum_c/sum)*Entropy_c;
disp(['菌褶间距的信息增益：',num2str(Gain_gillsize)])

%茎的形状
sum_t=1;yes=1;no=0;%菌褶间距远
Entropy_t=-(yes/sum_t)*log2(yes/sum_t)-0;
sum_e=9;yes=1;no=8;%菌褶间距近
Entropy_e=-(yes/sum_e)*log2(yes/sum_e)-(no/sum_e)*log2(no/sum_e);
Gain_gillsize=Entropy_S-(sum_t/sum)*Entropy_t-(sum_e/sum)*Entropy_e;
disp(['茎的形状的信息增益：',num2str(Gain_gillsize)])

结果如下：

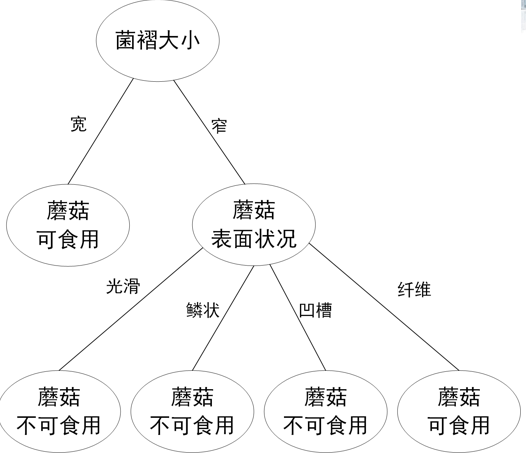
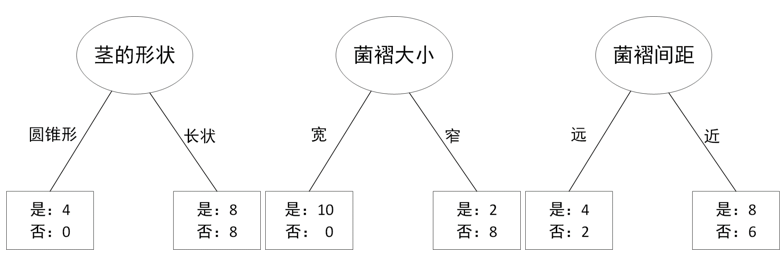
形成的决策树如下：