神经网络入门（详细 ）

文章目录

机器学习流程

机器学习需要人工选取数据，提取数据。
深度学习是机器学习的一部分。

• 数据获取
• 特征工程 数据特征决定了模型的上限 预处理和特征提取是最核心的 算法与参数选择决定了如何逼近这个上限
• 建立模型
• 评估与应用

传统特征提取方法：

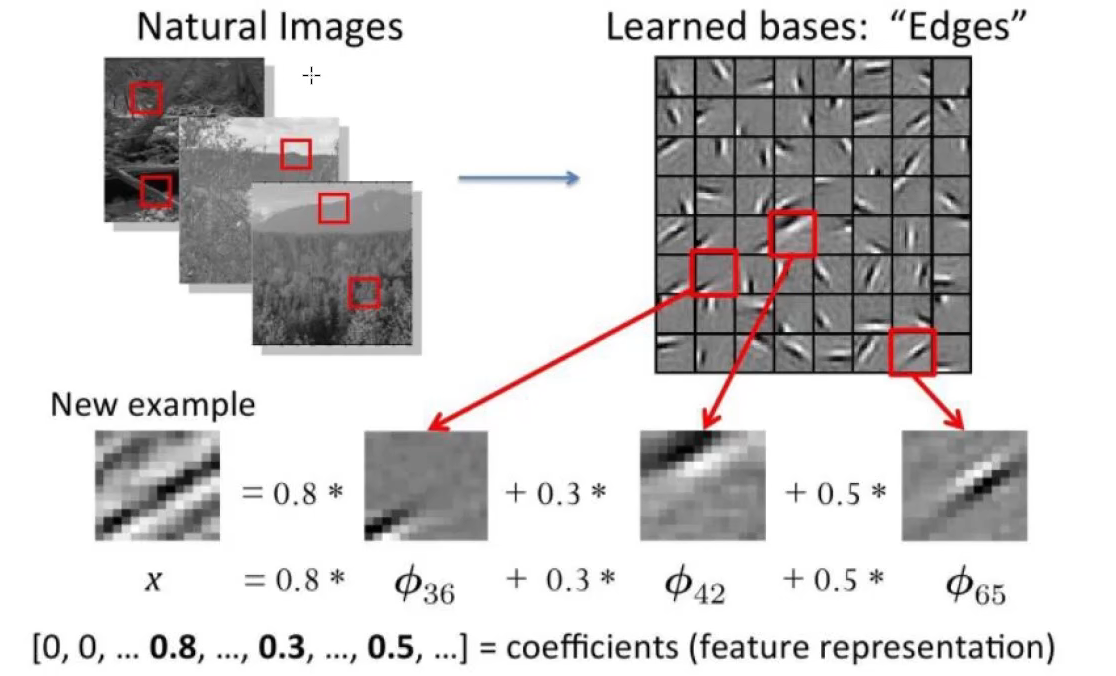
为什么需要深度学习

·解决核心是，如何去提取特征

图像分类

计算机视觉面临的挑战

• 照射角度
• 性状改变
• 部分遮蔽
• 背景混入

机器学习常规套路

1. 收集数据并给定标签
2. 训练一个分类器
3. 测试，评估

K近邻

K近邻算法

数据：两类点方块和三角
绿色的点属于方块还是三角呢？
K=3还是K=5？结果一样吗？

K近邻计算流程：

1. 就算已知类别数据集中的点与当前点的距离
2. 按照距离依次排序
3. 选取与当前点距离最小的K个点
4. 确定前K个点所在类别的出现概率
5. 返回前K个点出现频率最高的类别作为当前点预测分类

K近邻分析

KNN 算法本身简单有效，它是一种 lazy-learning 算法。
分类器不需要使用训练集进行训练，训练时间复杂度为0。
KNN 分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为 n，那么 KNN 的分类时间复杂度为O（n）。
K 值的选择，距离度量和分类决策规则是该算法的三个基本要素。

距离的选择：

L1 distance：

     d
    
    
     1
    
   
   
    (
   
   
    
     I
    
    
     1
    
   
   
    ,
   
   
    
     I
    
    
     2
    
   
   
    )
   
   
    =
   
   
    
     ∑
    
    
     p
    
   
   
    ∣
   
   
    
     I
    
    
     1
    
    
     p
    
   
   
    −
   
   
    
     I
    
    
     2
    
    
     p
    
   
   
    ∣
   
  
  
   d_1(I_1,I_2)=\sum_p \vert I_1^p - I_2^p \vert
  
 
d1​(I1​,I2​)=∑p​∣I1p​−I2p​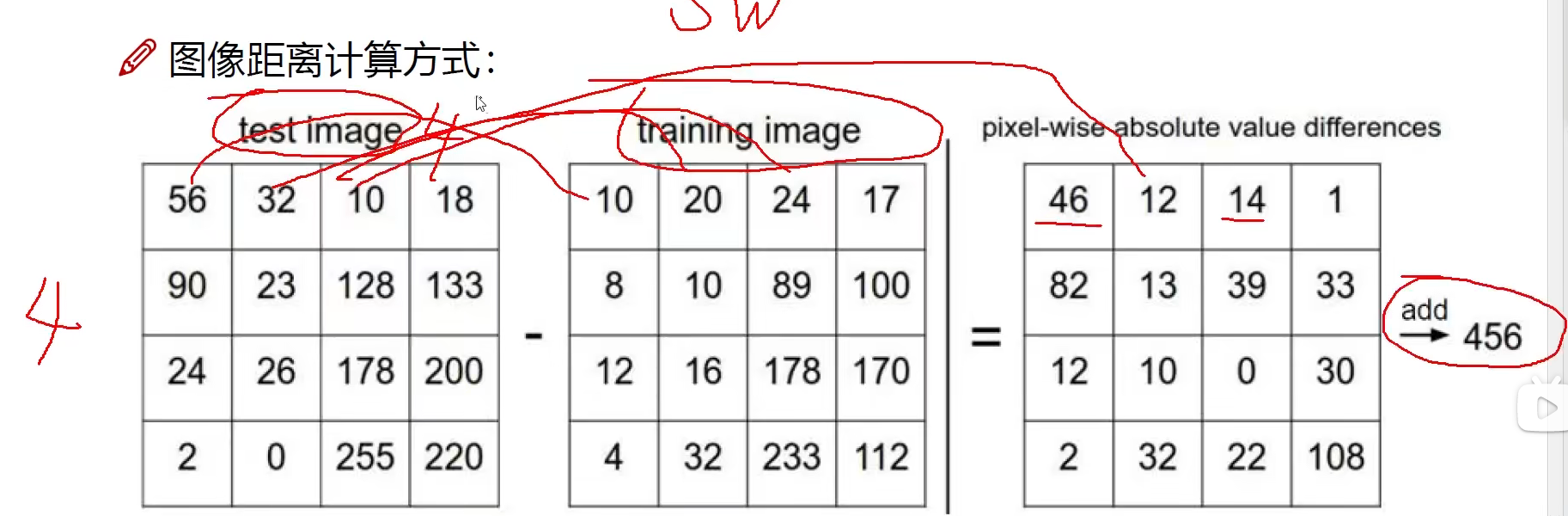∣![在这里插入图片描述](https://img-blog.csdnimg.cn/903712b8e3ba40dc91d9080d2b790eb8.png)

为什么K近邻不能用来图像分类？

背景主导是一个最大的问题，我们关注的却是主体（主要成分）
如何才能让机器学习到哪些是重要的成分呢？

神经网络基础

线性函数

从输入 --> 输出的映射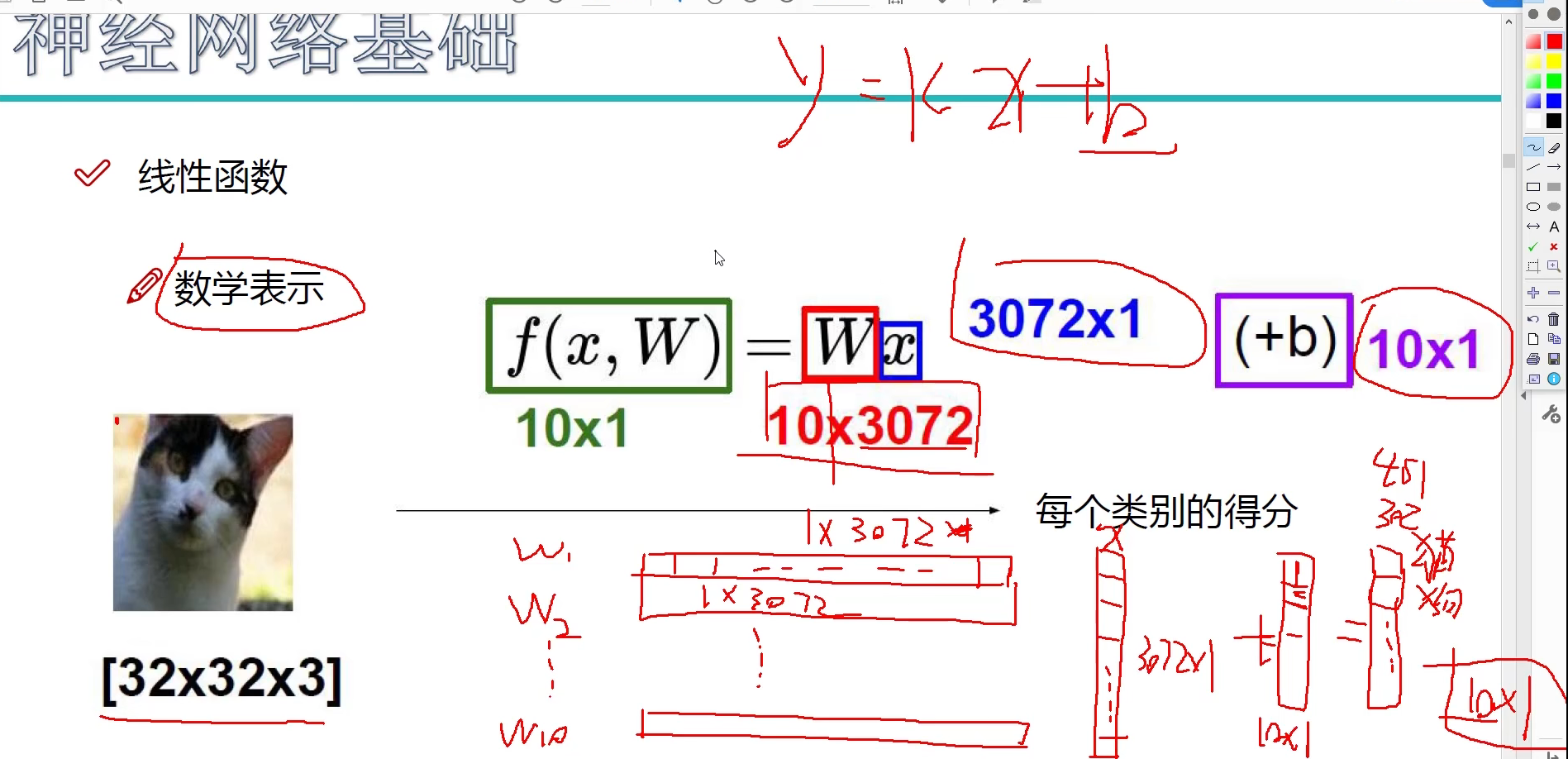

计算方法

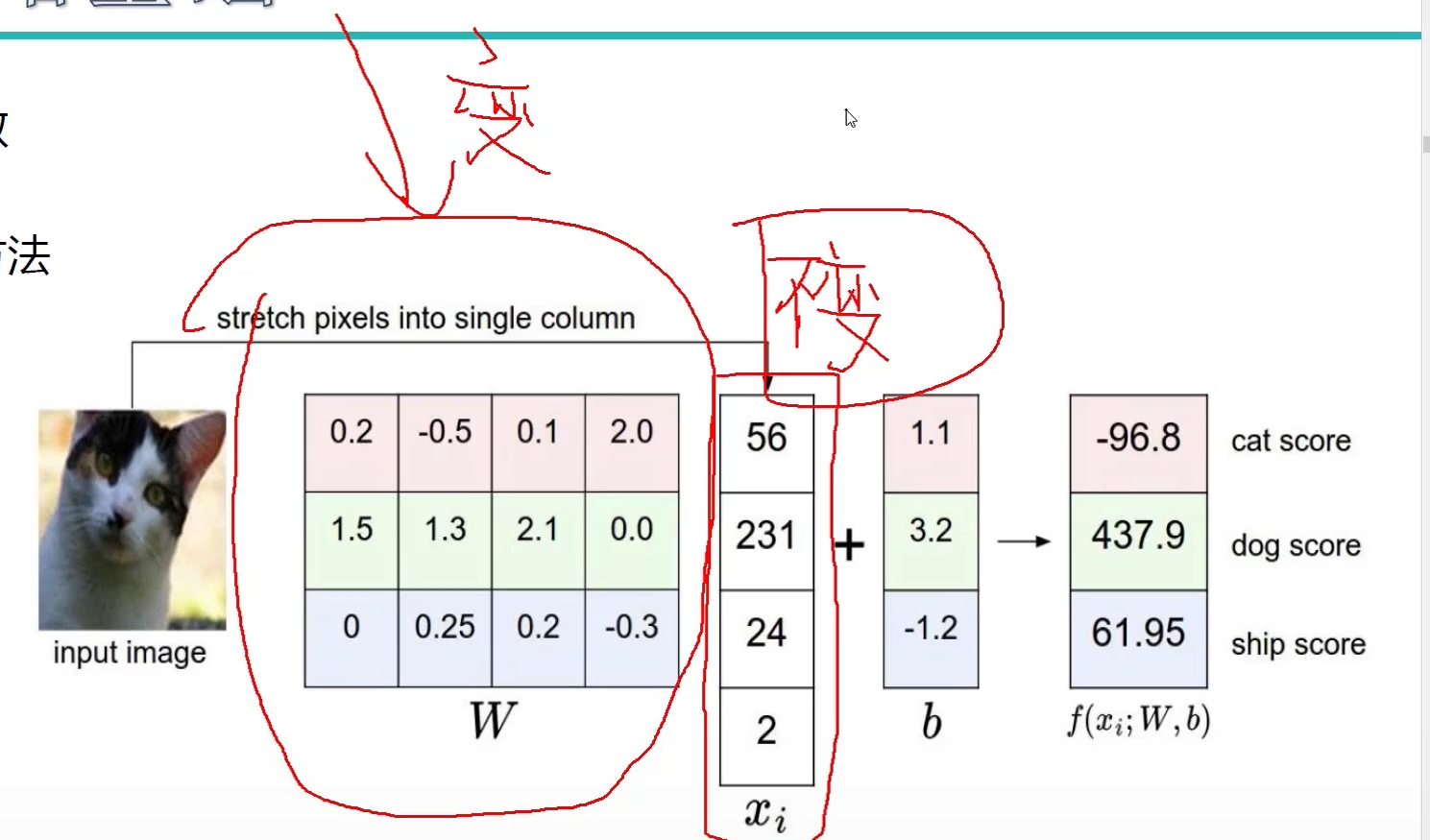
什么样的 W 更适合我们的预期目标

损失函数

如何衡量分类的结果呢？

结果的得分值有着明显的差异，我们需要明确的指导模型的当前效果，有多好或是多差！

如果损失函数的值相同，那么意味着两个模型一样吗？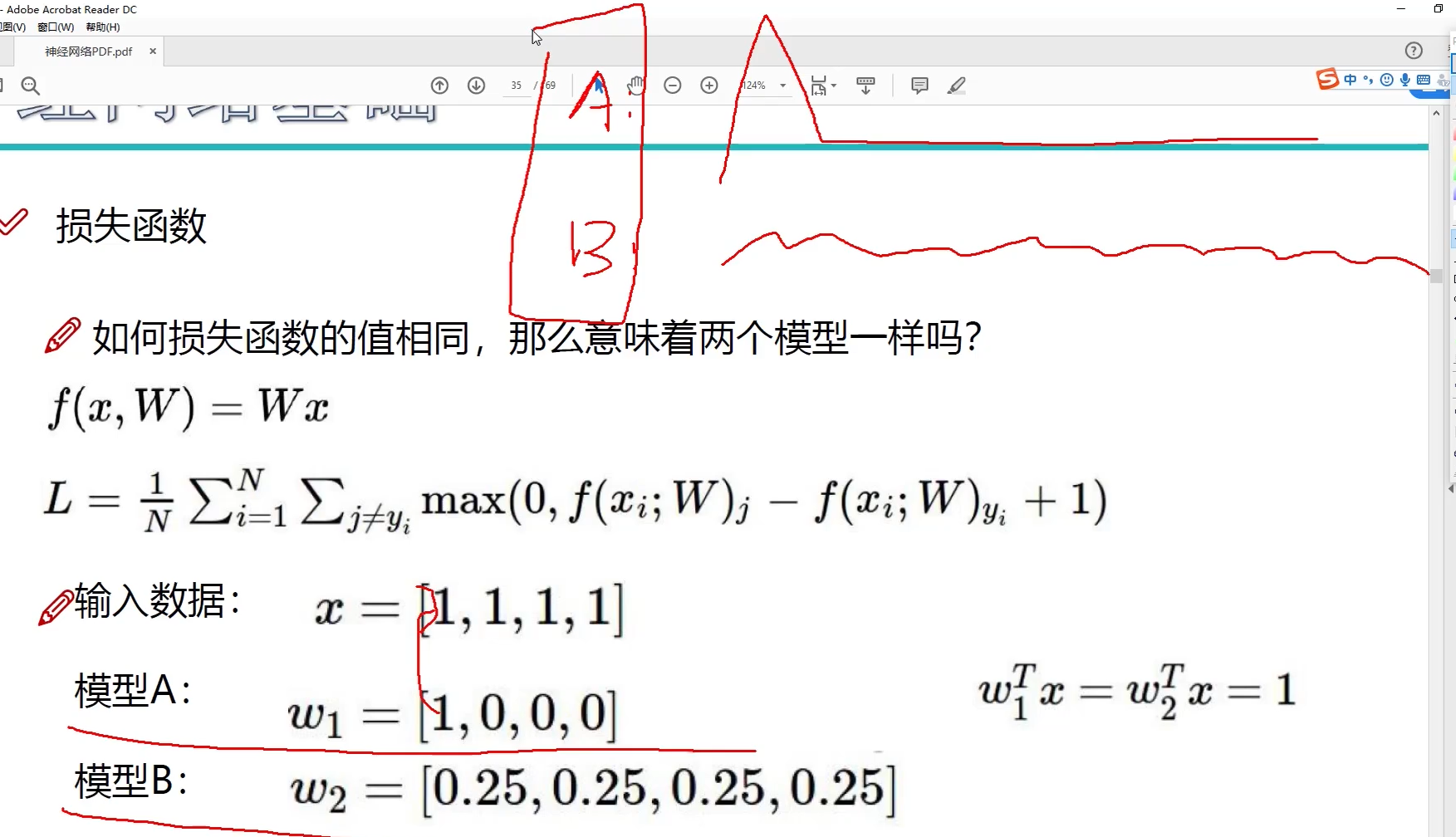

在训练过程中，关注权重参数是否会发生变异，发生过拟合

损失函数

     L
    
    
     i
    
   
   
    =
   
   
    
     ∑
    
    
     
      j
     
     
      ≠
     
     
      
       y
      
      
       i
      
     
    
   
   
    m
   
   
    a
   
   
    x
   
   
    (
   
   
    0
   
   
    ,
   
   
    
     s
    
    
     j
    
   
   
    −
   
   
    
     s
    
    
     
      y
     
     
      i
     
    
   
   
    +
   
   
    1
   
   
    )
   
  
  
   L_i=\sum_{j\ne y_i}max(0,s_j-s_{y_i}+1)
  
 
Li​=∑j​=yi​​max(0,sj​−syi​​+1)

损失函数其实有很多种，我们来实验一个

      S
     
     
      j
     
    
   
   
    S_j
   
  
 Sj​ 错误类别，
 
  
   
    
     
      S
     
     
      
       y
      
      
       i
      
     
    
   
   
    S_{y_i}
   
  
 Syi​​ 正确类别

 
  
   
    
     Δ
    
   
   
    \Delta
   
  
 Δ表示容忍程度

正则化惩罚项

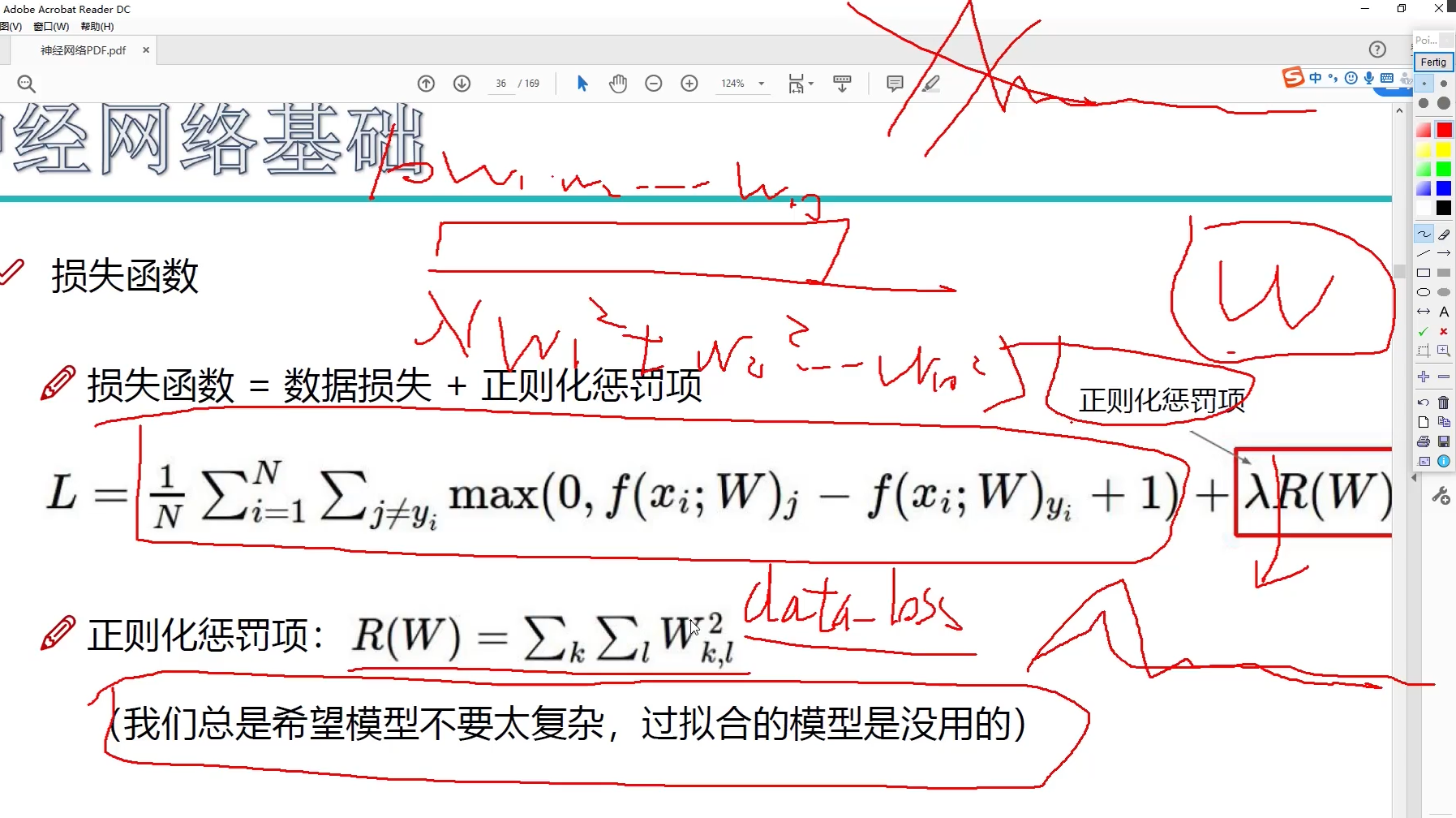
神经网络的缺点就是太强了

     λ
    
   
   
    \lambda
   
  
 λ越大，抑制效果越强

Softmax分类器

现在我们得到的是一个输入的得分值，但如果给我一个概率值岂不更好！

如何把一个得分值转换成一个概率值呢？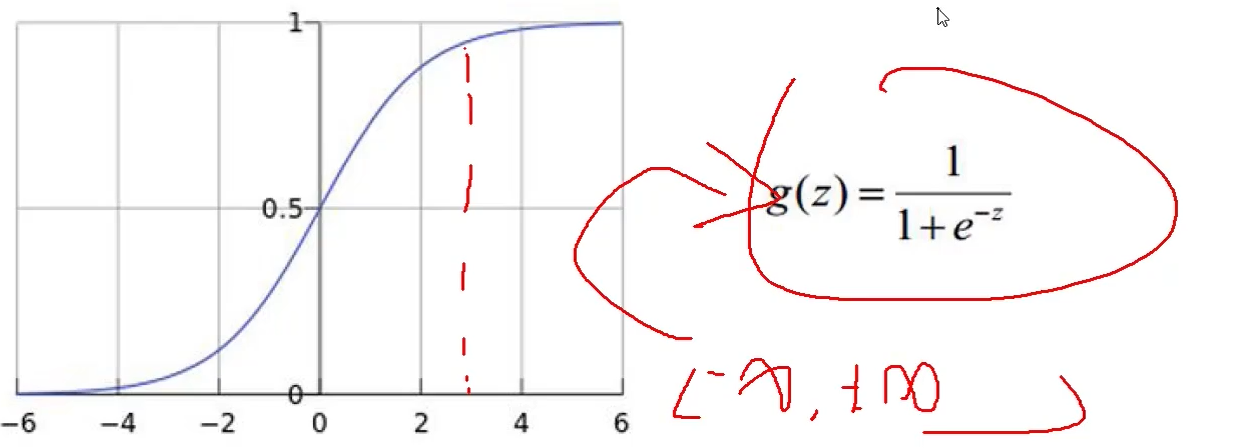

归一化：

    P
   
   
    (
   
   
    Y
   
   
    =
   
   
    k
   
   
    ∣
   
   
    x
   
   
    =
   
   
    
     x
    
    
     i
    
   
   
    )
   
   
    =
   
   
    
     
      
       e
      
      
       s
      
     
     
      k
     
    
    
     
      
       ∑
      
      
       j
      
     
     
      
       e
      
      
       s
      
     
     
      j
     
    
   
  
  
   P(Y=k|x=x_i)= {e^sk \over \sum_je^sj}
  
 
P(Y=k∣x=xi​)=∑j​esjesk​

 
  
   
  
  
   \qquad
  
 
where

 
  
     
  
  
   \;
  
 


 
  
   
    s
   
   
    =
   
   
    f
   
   
    (
   
   
    
     x
    
    
     i
    
   
   
    ;
   
   
    W
   
   
    )
   
  
  
   s=f(x_i;W)
  
 
s=f(xi​;W)

计算损失值：

     L
    
    
     i
    
   
   
    =
   
   
    −
   
   
    l
   
   
    o
   
   
    g
   
   
    P
   
   
    (
   
   
    Y
   
   
    =
   
   
    
     y
    
    
     i
    
   
   
    ∣
   
   
    X
   
   
    =
   
   
    
     x
    
    
     i
    
   
   
    )
   
  
  
   L_i=-logP(Y=y_i|X=x_i)
  
 
Li​=−logP(Y=yi​∣X=xi​)

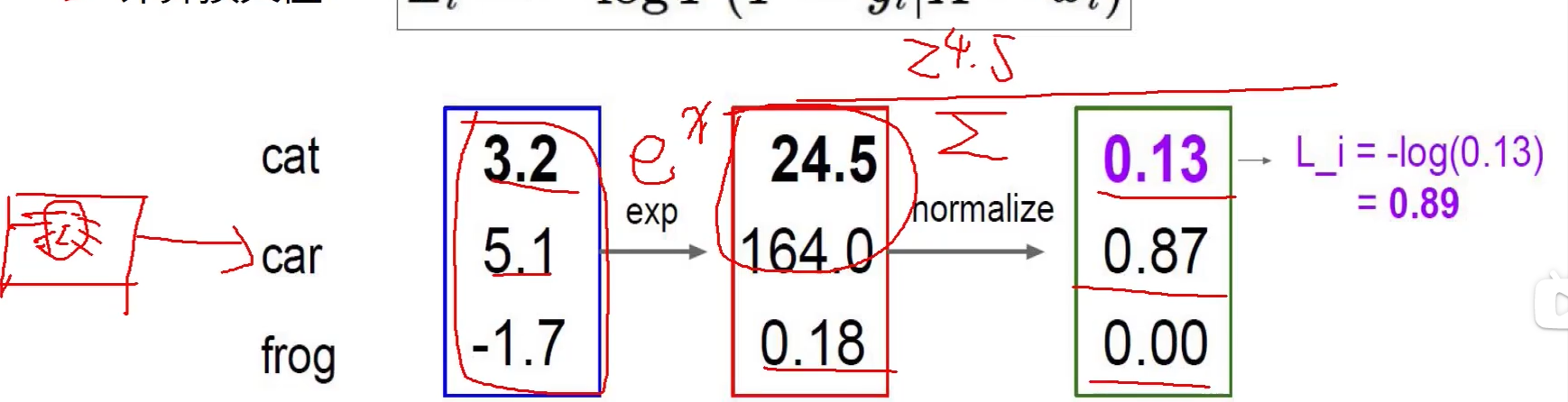
交叉熵损失函数
通过对数函数求损失

前向传播

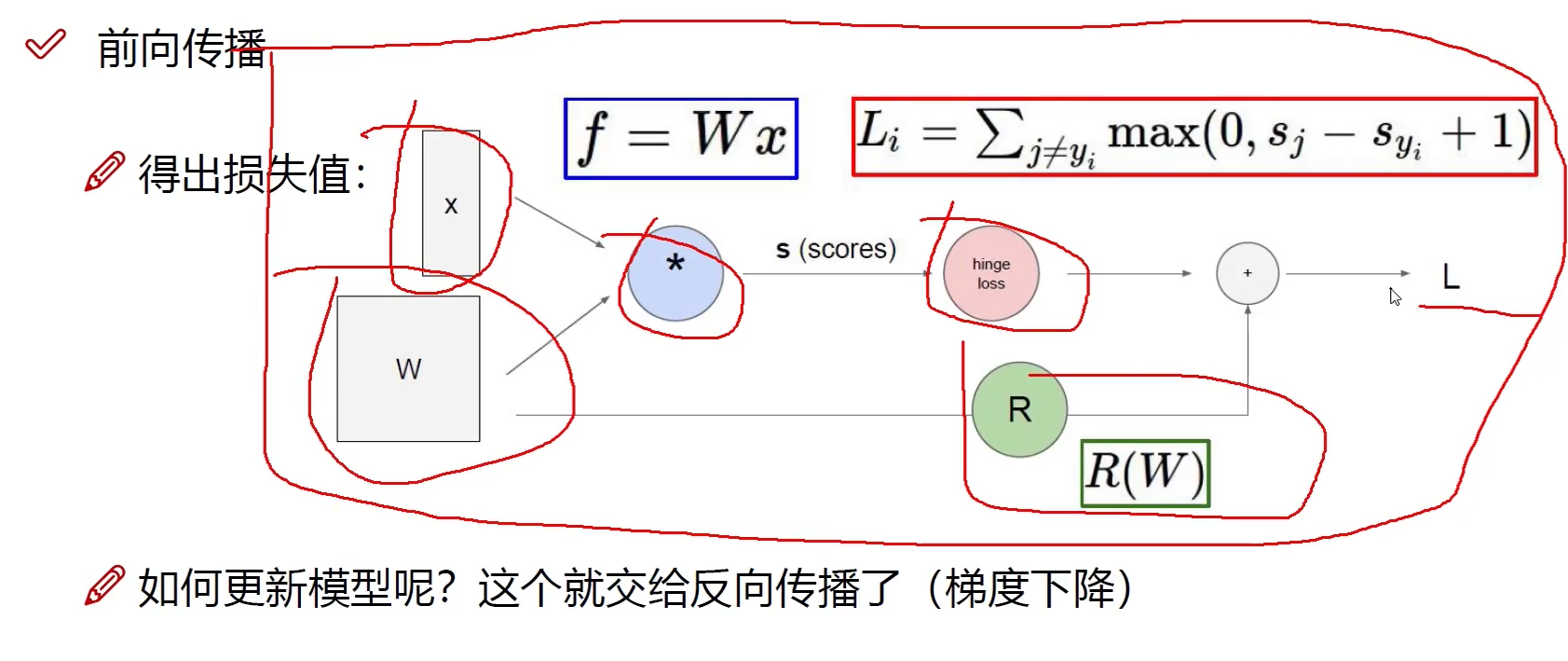
反向传播

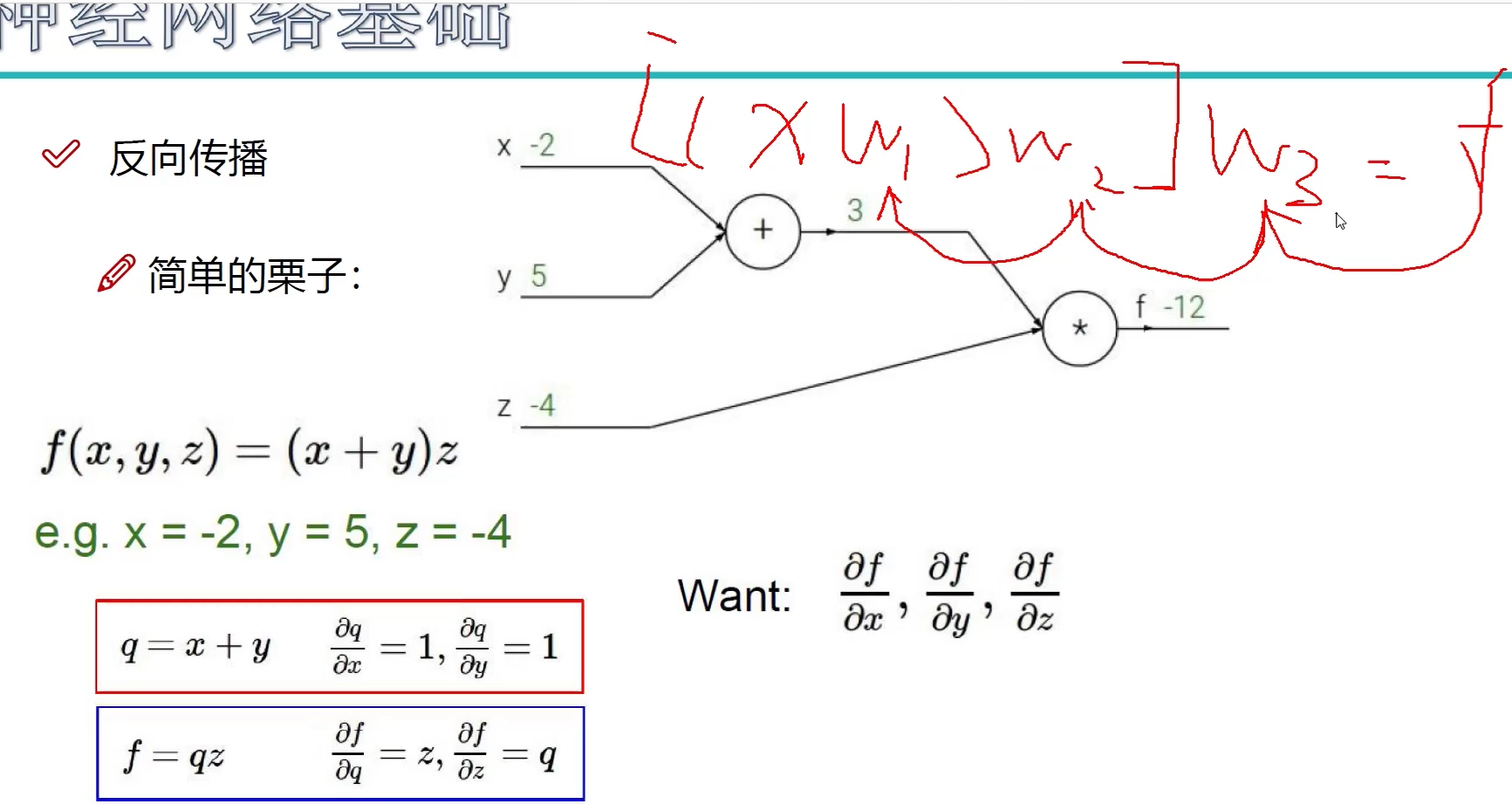
从后往前，逐层逐步传播

加法门单元：均等分配
MAX门单元：给最大的
乘法门单元：互换的感觉

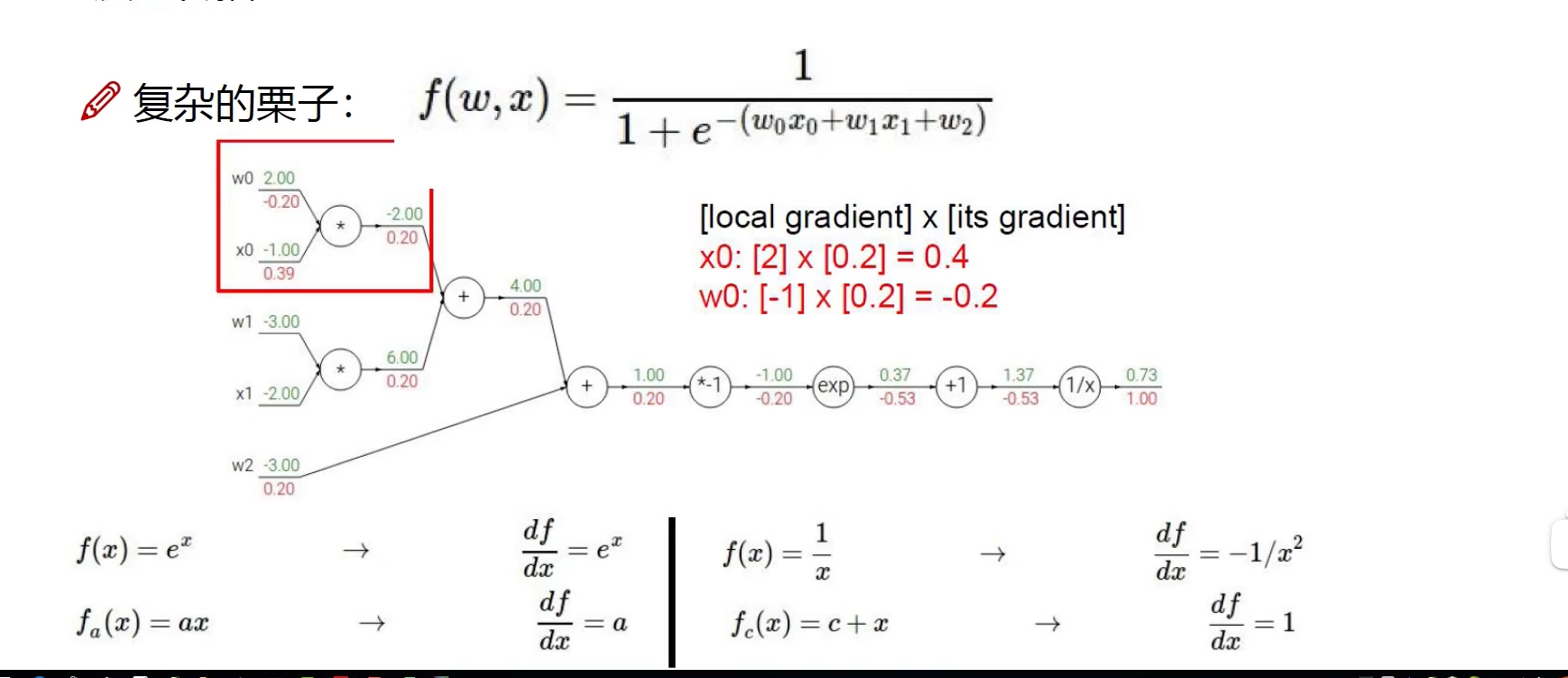
链式法则

梯度是一步一步传的
·

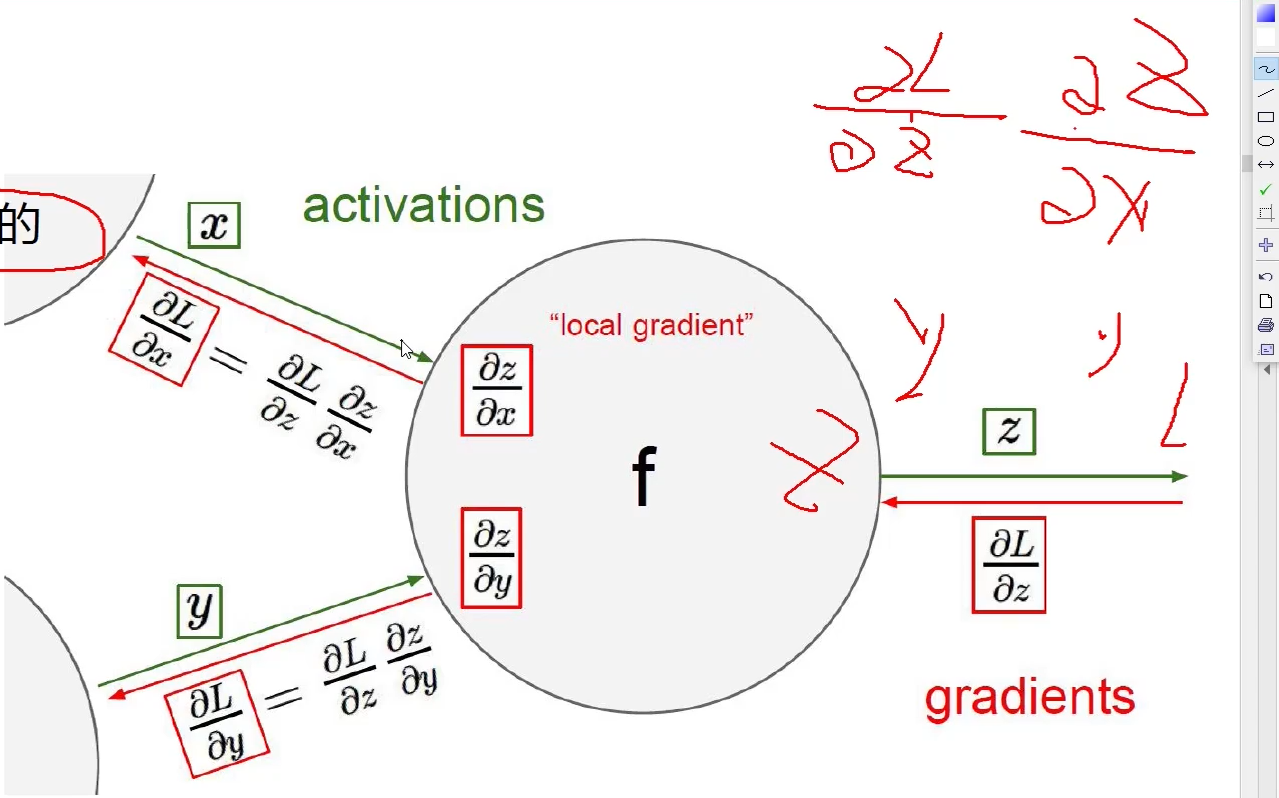
复杂的例子

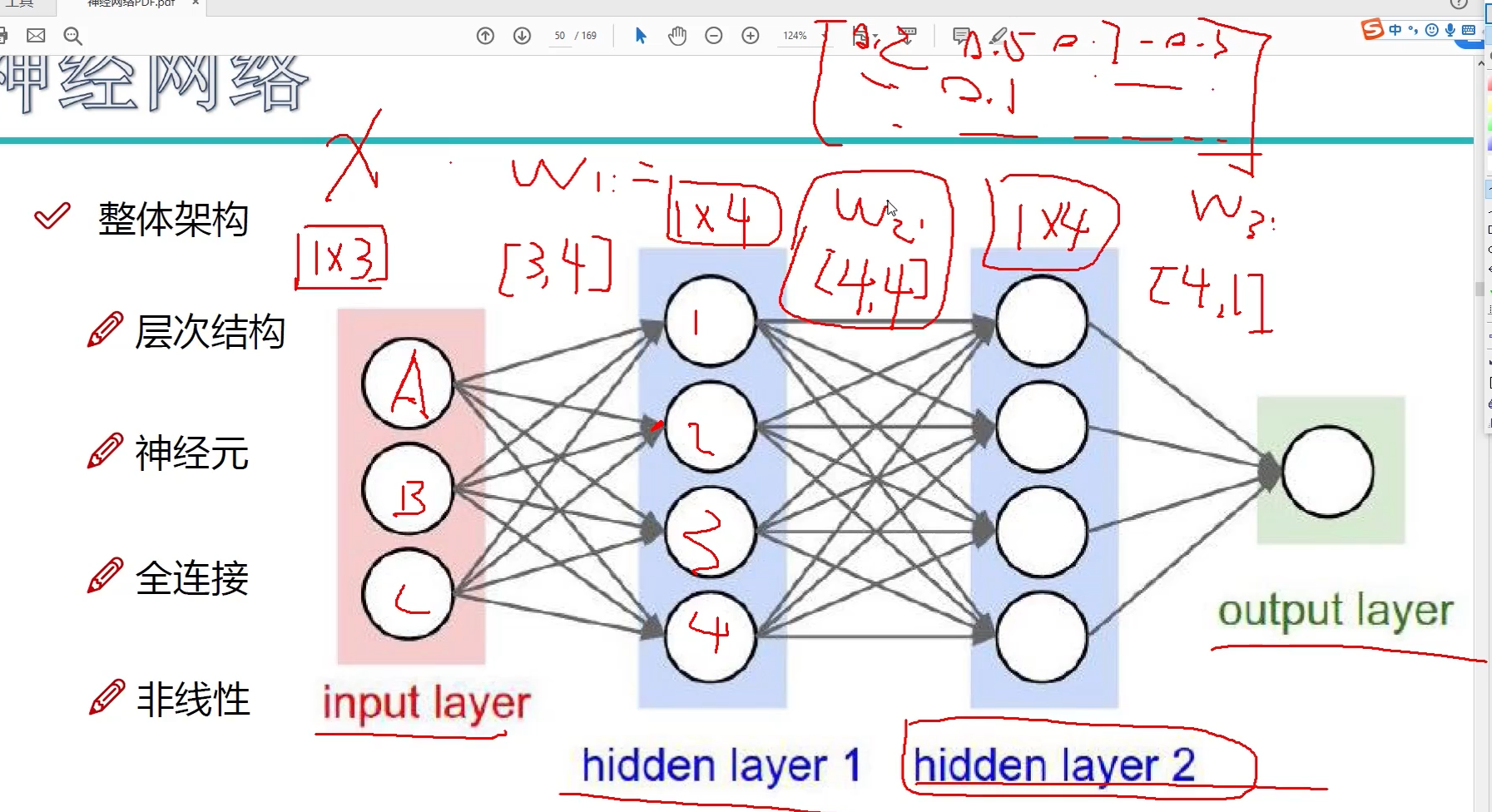
整体结构

非线性：激活函数sigmod、max、relu等

基本结构：

    f
   
   
    =
   
   
    
     W
    
    
     2
    
   
   
    m
   
   
    a
   
   
    x
   
   
    (
   
   
    0
   
   
    ,
   
   
    
     W
    
    
     1
    
   
   
    x
   
   
    )
   
  
  
   f=W_2max(0,W_1x)
  
 
f=W2​max(0,W1​x)

继续堆叠一层：

    f
   
   
    =
   
   
    
     W
    
    
     3
    
   
   
    m
   
   
    a
   
   
    x
   
   
    (
   
   
    0
   
   
    ,
   
   
    
     W
    
    
     2
    
   
   
    m
   
   
    a
   
   
    x
   
   
    (
   
   
    0
   
   
    ,
   
   
    
     W
    
    
     1
    
   
   
    x
   
   
    )
   
   
    )
   
  
  
   f=W_3max(0,W_2max(0,W_1x))
  
 
f=W3​max(0,W2​max(0,W1​x))

神经网络的强大之处在于，用更多的参数来拟合复杂的数据
(参数多到多少呢？百万级别都是小儿科，但是参数越多越好吗?)

神经元个数越多，得到的过拟合成对越大，在计算机上得到的效果可能会越好，运行速度相对会变慢。
https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html

正则化的作用

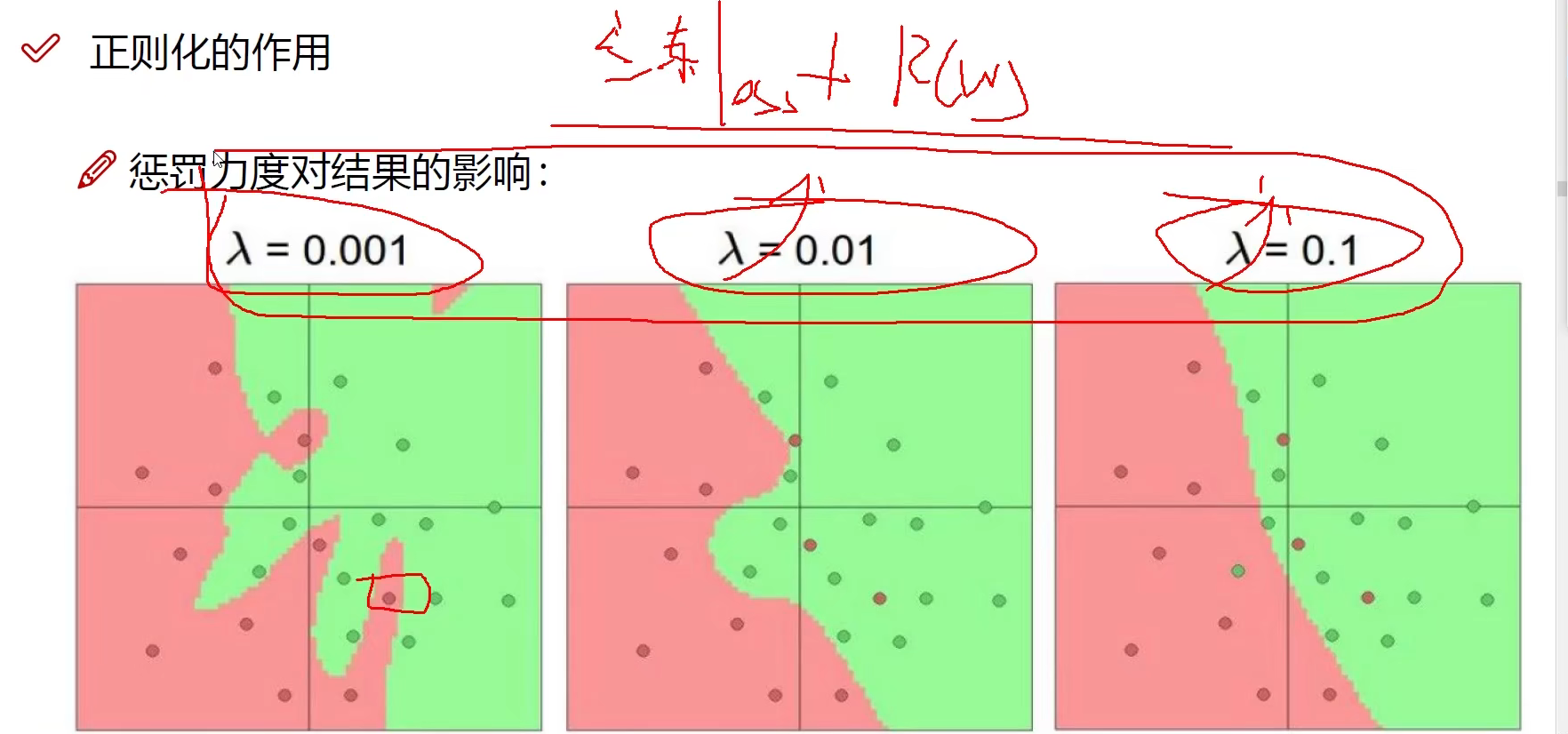
惩罚力度加大，W更加正常，边界更加平滑，防止过拟合

参数个数对结果的影响

激活函数

非常重要的一部分

常用的激活函数（Sigmoid,Relu,Tanh等）

激活函数对比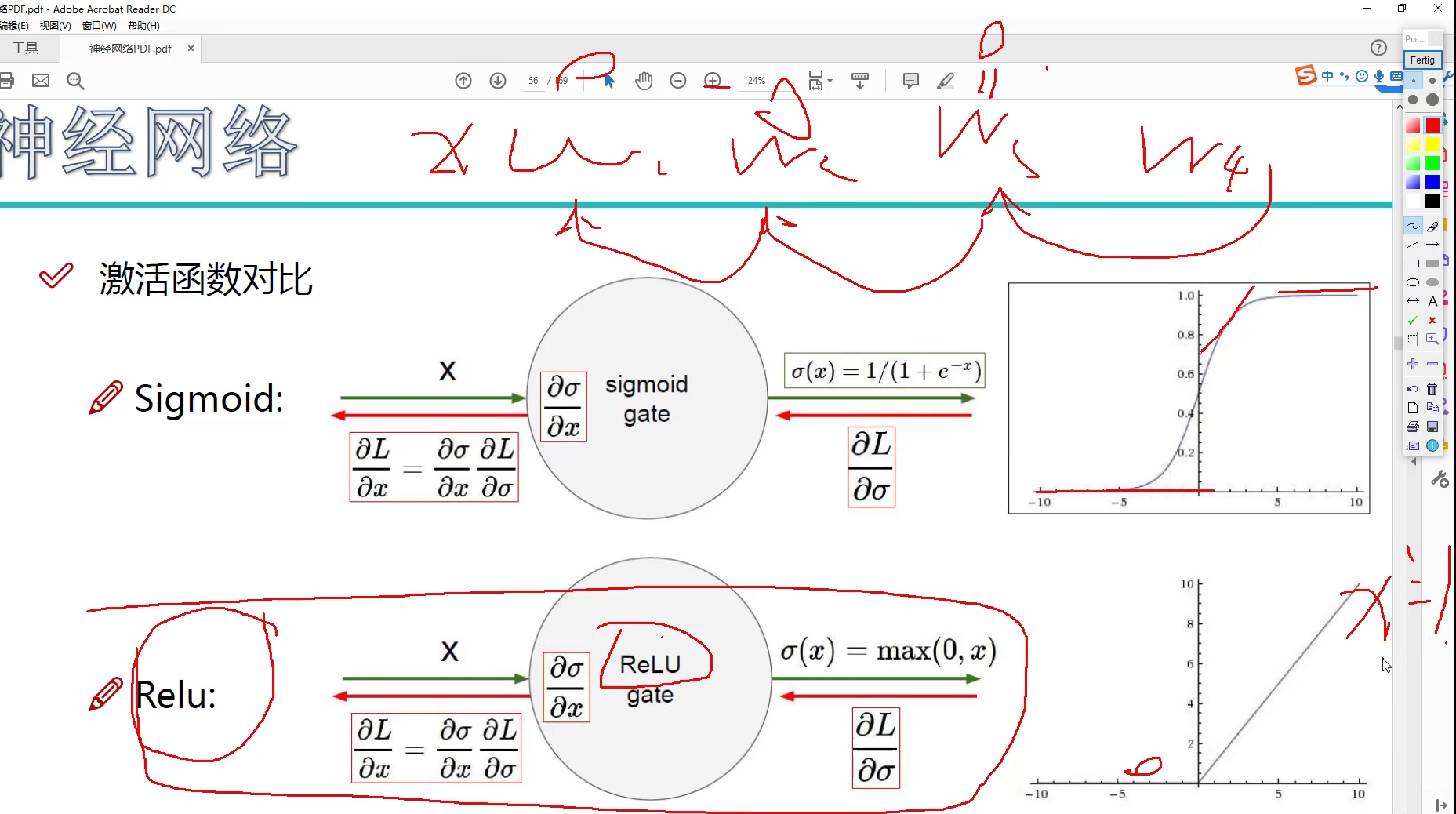

Sigmod 函数可能会造成梯度消失
现在市面上多采用 Relu 函数及其变式

数据预处理

不同的预处理结果会使得模型的效果发生很大的差异。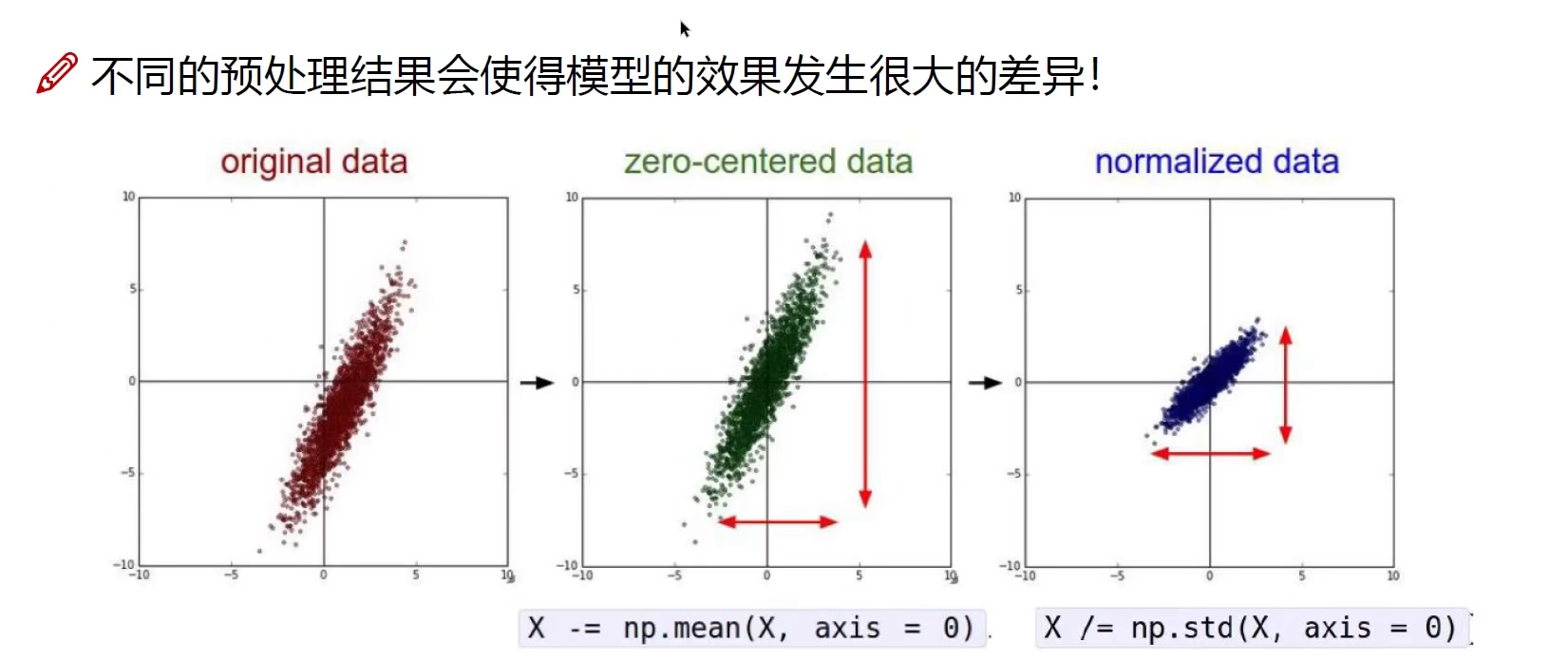

参数初始化

参数初始化同样非常重要

通常我们都使用随机策略来进行参数初始化

    W
   
   
    =
   
   
    0.01
   
   
    ∗
   
   
    n
   
   
    p
   
   
    .
   
   
    r
   
   
    a
   
   
    n
   
   
    d
   
   
    o
   
   
    m
   
   
    .
   
   
    r
   
   
    a
   
   
    n
   
   
    d
   
   
    n
   
   
    (
   
   
    D
   
   
    ,
   
   
    H
   
   
    )
   
  
  
   W = 0.01* np.random.randn(D,H)
  
 
W=0.01∗np.random.randn(D,H)

让W值尽可能比较小，平滑

DROP-OUT（传说中的七伤拳）

过拟合是神经网络非常头疼的一个大问题！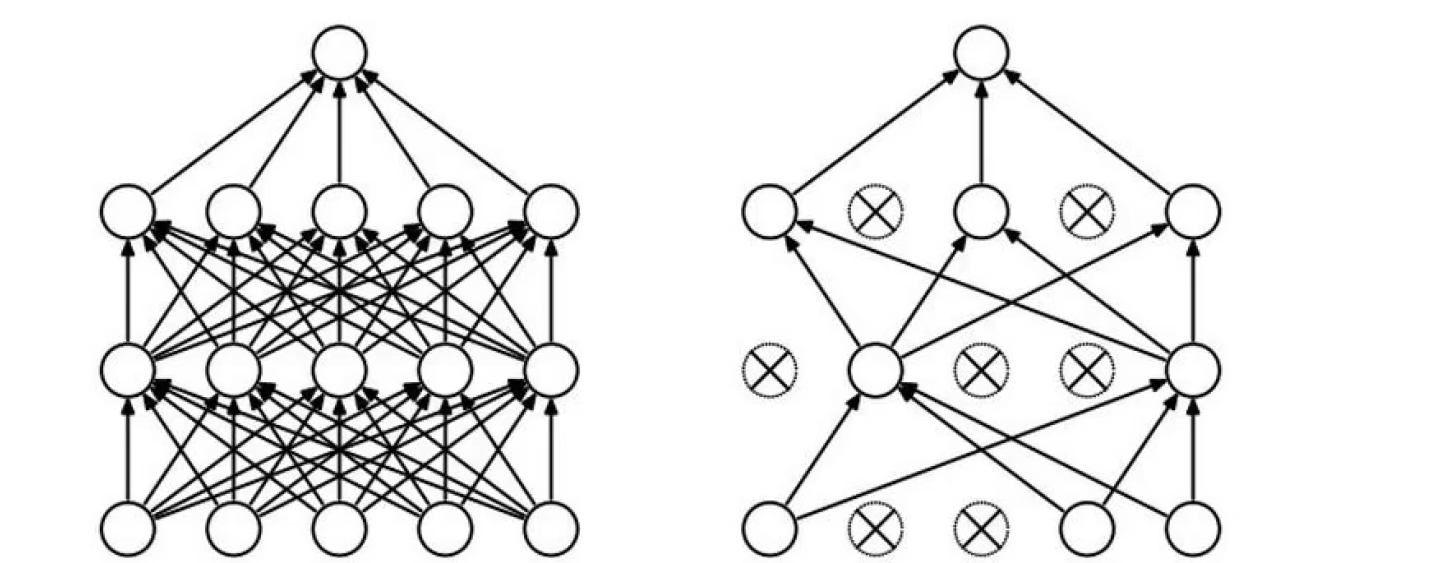

在每一轮训练中，随机选择一些神经元杀死。
在训练中，每层每一次随机选择一部分杀死。

线性回归

梯度下降

目标函数：

    J
   
   
    (
   
   
    
     θ
    
    
     0
    
   
   
    ,
   
   
    
     θ
    
    
     1
    
   
   
    )
   
   
    =
   
   
    
     1
    
    
     
      2
     
     
      m
     
    
   
   
    
     ∑
    
    
     1
    
    
     m
    
   
   
    (
   
   
    
     h
    
    
     θ
    
   
   
    (
   
   
    
     x
    
    
     
      (
     
     
      i
     
     
      )
     
    
   
   
    −
   
   
    
     y
    
    
     
      (
     
     
      i
     
     
      )
     
    
   
   
    )
   
   
    )
   
  
  
   J(\theta_0,\theta_1) = {1 \over 2m}\sum_{1}^m(h_\theta(x^{(i)}-y^{(i)}))
  
 
J(θ0​,θ1​)=2m1​∑1m​(hθ​(x(i)−y(i)))

寻找山谷的最低点，也就是我们的目标函数终点（什么样的参数能使得目标函数达到极值点）
下山分几步走呢？（更新参数）
（1）：找到当前最合适的方向
（2）：走那么一小步，走快了该“跌倒”了
（3）：按照方向与步伐去更新我们的参数