前言
- 最早的免疫系统起源于1973-1976年间Jerne的三篇关于免疫网络的文章
- 1986年Farmer在此基础上提出了基于网络的二进制的免疫系统
- 模拟生物免疫系统的抗原识别、细胞分化、记忆和自我调节功能的一类算法
遗传算法的思想简单讲就是父代之间通过交叉互换以及变异产生子代，不断更新适应度更高的子代，从而达到优化的效果。
而免疫算法本质上其实也是更新亲和度（这里对应上面的适应度）的过程，抽取一个抗原（问题），取一个抗体（解）去解决，并计算其亲和度，而后选择样本进行变换操作（免疫处理），借此得到得分更高的解样本，在一次一次的变换过程中逐渐接近最后解。
截止到 2023 年，算法引用趋势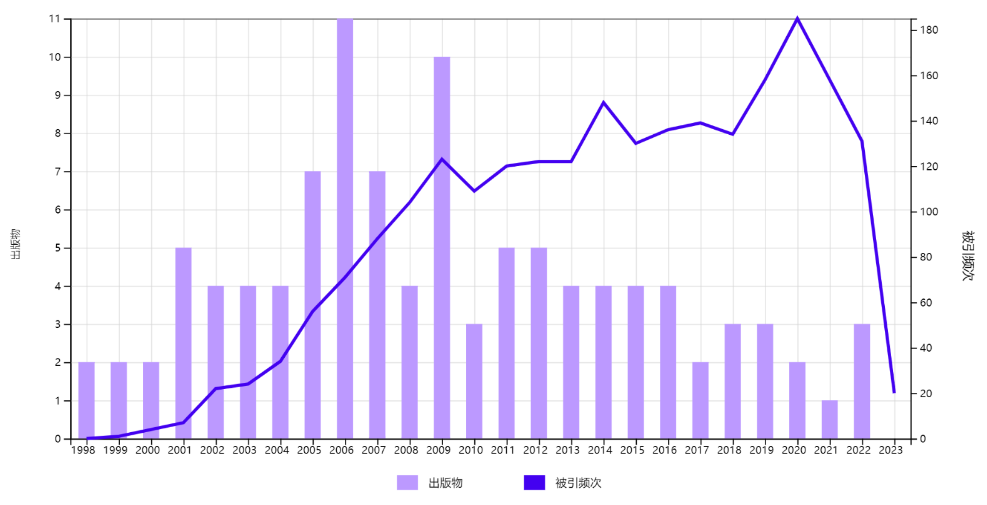
1. 免疫算法的生物原理
- 抗原: 被免疫系统看做异体,引起免疫反应的分子
- 抗体: 免疫系统用来鉴别和移植外援物质的一种蛋白质复合体.每种抗体只识别特定的目标抗原
- 淋巴细胞: 免疫系统中起主要作用的微小白细胞,包括B细胞和抗体,T细胞和细胞因子以及自然杀伤细胞
- B细胞: 全称是B淋巴细胞,在骨髓分化成熟,免疫系统的本质部分
- T细胞: 全称是T淋巴细胞,在胸腺分化成熟,按功能可以分为细胞毒T细胞(cytotoxic T cell), 辅助T细胞(helper T cell), 调节/抑制T细胞(regulatory/suppressor T cell)和记忆T细胞(memory T cell)
- 亲和力: 抗体和抗原，抗体和抗体之间的相似程度
- 记忆细胞: 指亲和力大于指定阈值的抗体
2. 免疫系统模型
- 把重心放在B细胞表层的抗体和抗原之间的机制上
- 抗体和抗原的亲和程度由它的抗体决定簇和抗原的决定基的匹配程度决定假设每个抗原和每个抗体型分别只有一个抗原决定簇（实际它们都有许多不同类型的抗原决定基）
- 通过这些决定基之间的匹配程度控制不同类型抗体的复制和减少,以达到优化系统的目的.
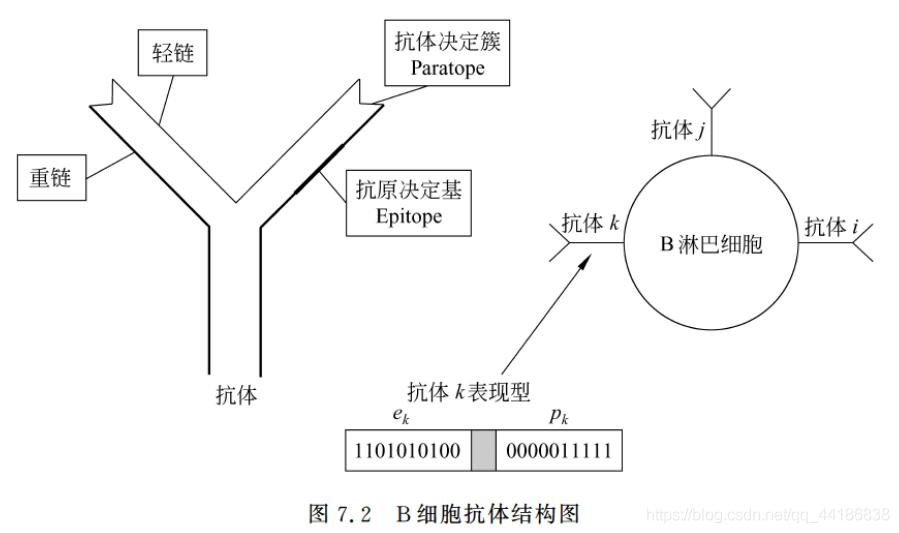
3. 免疫算法基本流程
3.1 基本组件
3.2 算法流程
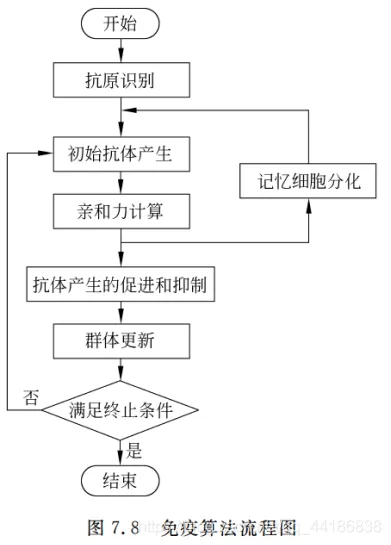
3.3 免疫算法的七个要素
识别抗体，生成初始化的抗体，计算亲和度，记忆细胞分化，抗体促进和抑制，产生新的抗体，结束条件。
1. 识别抗体
把目标函数和约束作为抗体。
2. 生成初始化的抗体
随机生成独特型串维数为 M 的 N 个抗体。
3. 计算亲和度
这个步骤可以说是免疫算法的重点，同时也是最难点。
（1） 抗体
v
v
v 和抗原的亲和度为
a
x
v
ax_v
axv
a
x
v
=
1
1
+
o
p
t
v
ax_v = \frac{1}{1 + opt_v}
axv=1+optv1
其中
o
p
t
v
opt_v
optv 表示抗体
v
v
v 和抗原的结合强度，对最优化问题，可以用抗体
v
v
v 的独特型的解和已知的最优解的相似程度表示，例如对函数
f
=
x
1
2
+
x
2
2
+
x
3
3
,
x
i
∈
[
−
10
,
10
]
,
i
=
1
,
2
,
3
,
.
.
.
f = x_1^2 + x_2^2 + x_3^3, x_i \in [-10, 10], i = 1, 2, 3, ...
f=x12+x22+x33,xi∈[−10,10],i=1,2,3,... 求最优解，已知的最优解是
0
0
0，那么抗体
v
v
v 的
o
p
t
v
opt_v
optv 就是其所代表的解在函数下的适应值。若是一个最大化问题，则
o
p
t
v
=
∣
f
v
−
f
m
a
x
f
m
a
x
∣
opt_v = |\frac{f_v - f_{max}}{f_{max}}|
optv=∣fmaxfv−fmax∣. 其中
f
m
a
x
f_{max}
fmax 是最优解的适应值，
f
v
f_v
fv 是抗体
v
v
v 的适应值。
（2）抗体
v
v
v 和抗体
w
w
w 的亲和度为：
a
y
v
,
w
=
1
1
+
E
(
2
)
ay_{v, w} = \frac{1}{1 + E(2)}
ayv,w=1+E(2)1
其中
E
(
2
)
E(2)
E(2) 为
v
v
v 和
w
w
w 的平均信息熵。通过这些平均信息熵，算法实现了多样化。下面简单介绍一下信息熵。基因的信息熵如图 7.9 所示
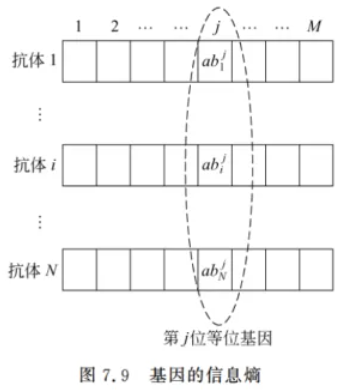
免疫系统有
N
N
N 个抗体，有
M
M
M 个基因(或独特型串的长度为
M
M
M), 第
j
j
j 个基因的信息熵为
E
j
(
N
)
:
E_j(N):
Ej(N):
E
j
(
N
)
=
∑
i
=
1
N
−
p
i
j
l
o
g
K
p
i
j
E_j(N) = \sum_{i=1}^N -p_{ij} log_K p_{ij}
Ej(N)=i=1∑N−pijlogKpij
其中
K
K
K 表示独特型串的字母表的长度，若为二进制数就是 2，
p
i
j
p_{ij}
pij 表示选择第
i
i
i 个抗体的第
j
j
j 位等位基因的概率，很明显
∑
i
=
1
N
p
i
j
=
1
\sum_{i=1}^N p_{ij} = 1
∑i=1Npij=1, 所以代表多样性的平均信息熵
E
(
N
)
E(N)
E(N) 为：
E
(
N
)
=
1
M
∑
j
=
1
M
E
j
(
N
)
E(N) = \frac{1}{M} \sum_{j=1}^M E_j(N)
E(N)=M1j=1∑MEj(N)
（4）记忆细胞分化
同人的免疫系统基本一致。
与抗原有最大亲和度的抗体加入了记忆细胞。由于记忆细胞数目有限，因此新生成的抗体将会代替记忆细胞中和它有最大亲和力者。
（5）抗体促进和抑制
最开始我介绍免疫算法其实就有提到这个。
通过计算抗体
v
v
v 的期望值，消除那些低期望值的抗体。
抗体
v
v
v 的期望值
e
v
e_v
ev 的计算公式为亲和度除以抗体
v
v
v 的密度：
e
v
=
a
x
v
c
v
e_v = \frac{ax_v}{c_v}
ev=cvaxv
其中抗体
v
v
v 的密度的计算方法如下：
c
v
=
−
q
k
N
c_v = -\frac{q_k}{N}
cv=−Nqk
其中
q
k
q_k
qk 表示和抗体
k
k
k 有较大亲和力的抗体。**通过这个公式能有效地抑制抗体的过分相似，避免算法的未成熟收敛。**
（6）产生新的抗体
这里就对应我最开始提到的遗传算法和免疫算法相似地方了。
基于不同抗体和抗原亲和力的高低，使用轮盘赌的方法 ，选择两个抗体。然后把这两个抗体按一定变异概率做变异，之后再做交叉，得到新的抗体。重复操作（6）知道产生所有N个新抗体。可以说免疫算法产生新的抗体的过程需要遗传算子的辅助。
（7）结束条件
如果求出的最优解满足一定的结束条件，则结束算法。
4. 算法特点
通过模仿免疫系统抗体与抗体之间的抑制和促进，让解向量相互之间产生对抗，有效的避免解向量过于相似所产生的过早收敛
5. 算法相关改进
主要分为两个大类
- 基本免疫算法与其他算法的融合- 最典型的是具有良好效果的免疫遗传算法- 免疫算法与蚁群算法、粒子群算法等多种进化算法都有混合算法
- 在初始免疫系统上重新建模，采取免疫系统的其他特征- 负选择算法- 克隆选择算法
References
[1] 一文搞懂什么是免疫算法Immune Algorithm【详细介绍】
[2] 浅谈人工免疫算法
[3] 免疫算法（Immune Algorithm)详解
本文转载自: https://blog.csdn.net/qq_46450354/article/details/130026201
版权归原作者 青年有志 所有， 如有侵权，请联系我们删除。
版权归原作者 青年有志 所有， 如有侵权，请联系我们删除。