时间序列的数据分析(七)：数据变换

之前已经完成了六篇关于时间序列的博客，还没有阅读过的读者请先阅读：

1. 时间序列的数据分析(一):主要成分
2. 时间序列的数据分析(二):数据趋势的计算
3. 时间序列的数据分析(三):经典时间序列分解
4. 时间序列的数据分析(四):STL分解
5. 时间序列的数据分析(五):简单预测法
6. 时间序列的数据分析(六):指数平滑预测法

数学变换

在之前的博客中我们介绍了时间序列的加法季节性和乘法季节性，在加法季节性的时间序列数据中，季节性波动的幅度或者趋势周期项的波动不随时间序列水平的变化而变化，如下图所示：

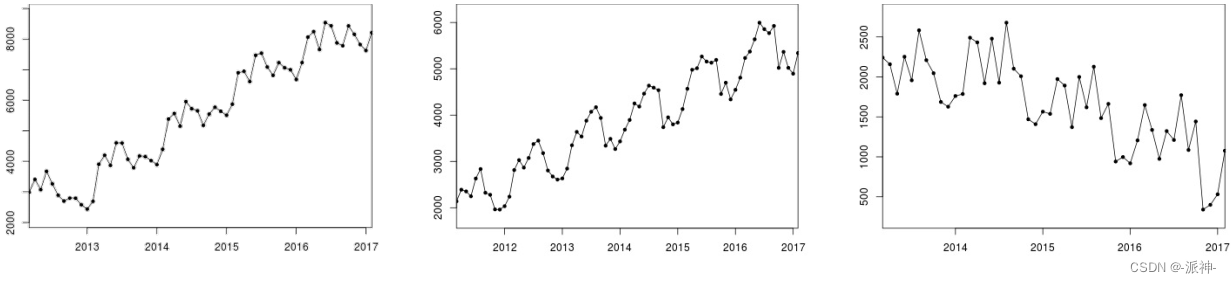
加法季节性的表达为：

在上式中 表示时间序列数据，表示季节项，表示趋势-周期项，表示残差项。

在乘法季节性的时间序列中，季节项或趋势周期项的变化与时间序列的水平成比例，如下图所示：

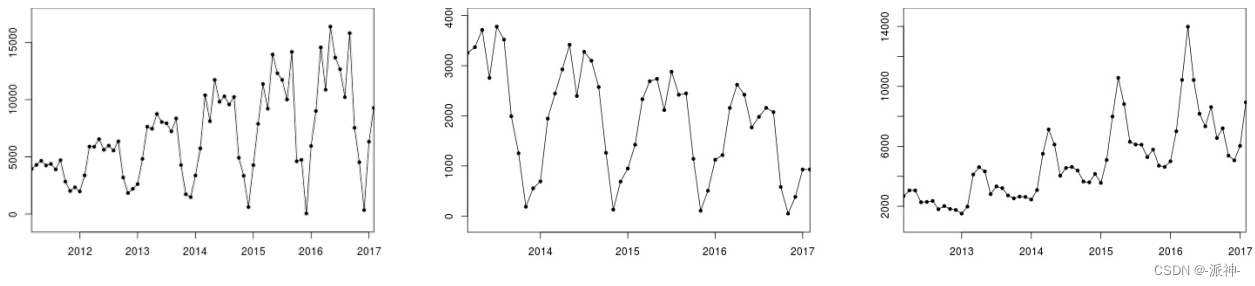
乘法季节性的表达式为：

为了对时间序列数据进行预测，我们需要对时间序列数据的主要成份进行分解，这个在之前的博客中都有介绍，对于乘法分解一般会使用对数法对数据进行转换，这会使得计算更加简单：首先对数据进行对数变换，直到时间序列随时间的波动趋于稳定，然后再使用加法分解。显然，采用对数变换的加法模型，等价于乘法模型：

等价于

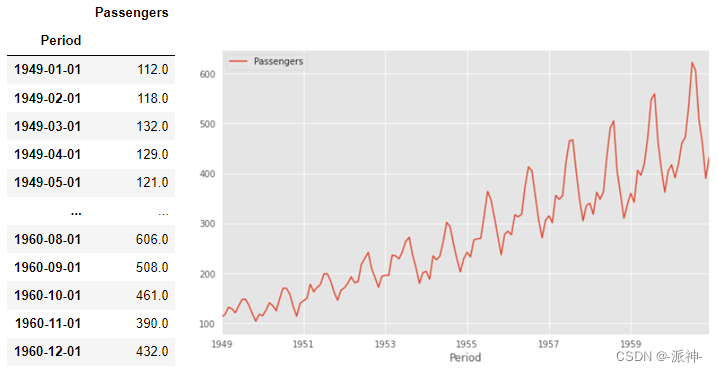
下面我们来使用航空公司乘客数据来实现对数变换，看看变换前后的数据差异：

#变换前的原始数据
df=pd.read_csv("airline_Passengers.csv")
df.plot();

下面采用numpy的log函数对数据进行对数变换：

#使用对数变换法的数据
df.Passengers=np.log(df.Passengers)
df.plot();

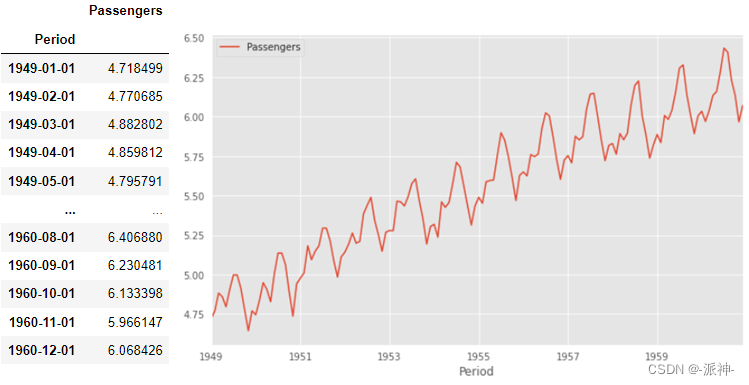
很明显经过对数变换以后，季节性乘法的周期变化幅度趋向于均衡，不再与时间变化成比例。假如我们把原始观测值记作 ，变换后的观测值记作，则。对数变换之所以有用，是因为它们易于解释：对数值的变化是原始值的相对（或百分比）变化。假设进行以10为底的对数变换，那么对数值加1相当于原始值乘以10。对数变换的另一个特点在于能够限制在原来测度下的预测值为正数。有时候其他变换也会被用到（虽然它们不是那么容易解释），例如平方根和立方根变换，它们也被称作幂变换，因为可以以的形式表示。

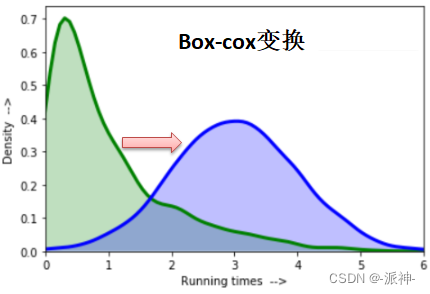
“Box-cox变换”是一个既包含对数变换，又包含幂变换的依赖于参数 的变换族，其定义如下：

Box-cox变换中的对数变换通常以自然对数e为底，因此如果，进行自然对数变换，否则，进行幂变换，然后简单缩放。下面我们使用python的scipy包的boxcox方法对上面的航空公司乘客数据进行变换，我们设置不同的值比如0，-2,2，以及不设置值，当不设置时算法会自动拟合出最优的值，下面我们看看不同的对数据产生的影响：

from scipy import stats

# 将λ设置为0,-2,2,不设置
df['tfmd_log'] =stats.boxcox(df.Passengers,lmbda=0)
df['tfmd_lmd_minus_2'] =stats.boxcox(df.Passengers,lmbda=-2)
df['tfmd_lmd_plus_2']=stats.boxcox(df.Passengers,lmbda=2)
df['tfmd_optimal_lmd'],lmbda_=stats.boxcox(df.Passengers)
print(f"最优 {lmbda_=}")

labels=['raw data','λ=0','λ=-2','λ=2','optimal λ=0.148']
data=[df.Passengers,df.tfmd_log,df.tfmd_lmd_minus_2,
       df.tfmd_lmd_plus_2,df.tfmd_optimal_lmd]
fig = plt.figure(figsize=(16,12))

for i in range(5):
    plt.subplot(3, 2, i+1)
    plt.plot(df.index,data[i],label=labels[i]);
    plt.legend();
plt.show();

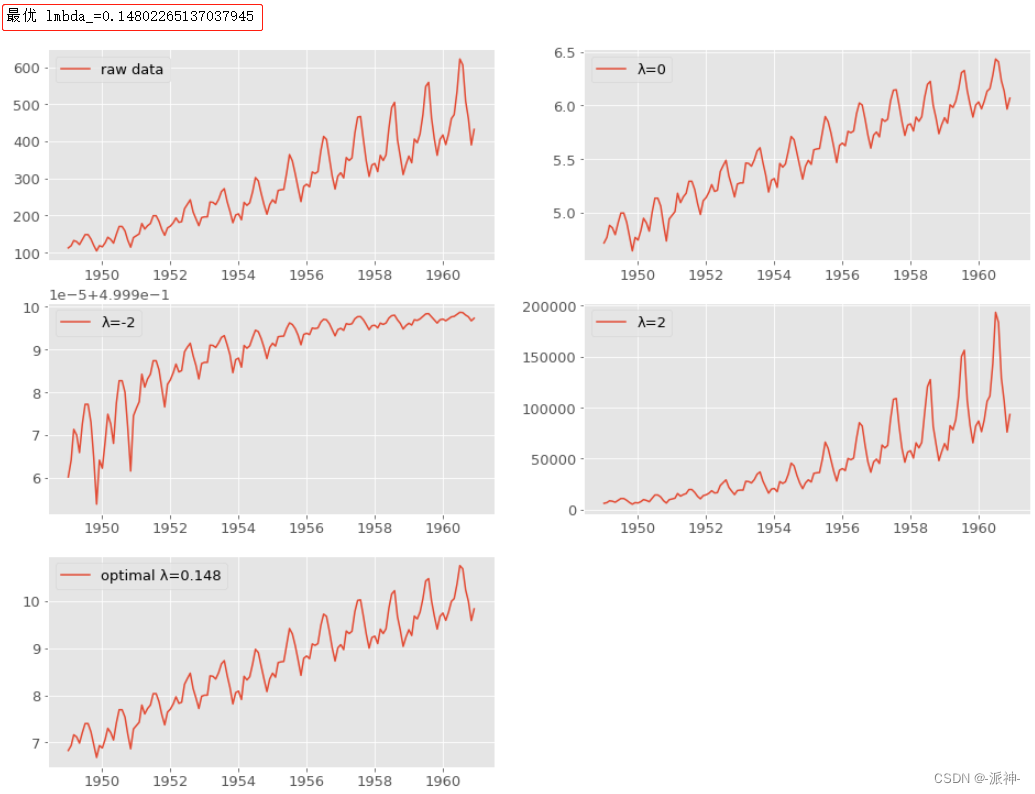
如上图所示，当我们将设置为较大的正直和较小的负值(如-2和2)时，顶部和底部的数据的形状发生了变形，而=0时做了对数变换这使得数据的季节性周期变换幅度得到了较好的调整。但这不是最优的调整，算法自动拟合出来的最优=0.148，这是理论上的最优值。完成数据变换以后，我们需要利用变换后的数据进行预测，得出预测值后，我们需要进行逆变换得到原始测度上的预测值。逆Box-Cox变换如下表示:

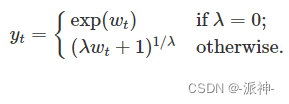
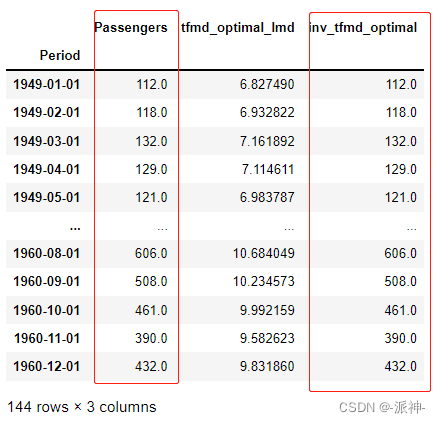
下面我们使用python的scipy包对上面的航空公司乘客变换数据进行逆变换，看看经过逆变换以后的数据与原始数据是否一致：

from scipy.special import inv_boxcox

lmbda_= 0.14802265137037945
df['inv_tfmd_optimal']=inv_boxcox(df['tfmd_optimal_lmd'],lmbda_)
df[['Passengers','tfmd_optimal_lmd','inv_tfmd_optimal']]

从上面的结果可知，经过逆变换后的数据与原始数据完全相等。

幂变换的特点

• 如果出现部分 ，除非给所有观测值加上一个常数，否则不能进行幂变换，。
• 选择一个简单的值会让解释更容易。
• 预测结果对值相对不敏感
• 很多情况下不需要进行变换
• 有时候变换对于预测结果影响不大，但对预测区间有很大影响。

总结

今天我们学习了时间序列数据的数学变换方法：简单对数变换以及Box-cox变换，我们使用了python的scipy包的boxcox和inv_boxcox方法对时间序列数据进行了数学变换和逆变换，对数据进行数学变换的目的是为了让乘法季节性的周期性变化幅度大致相同,即周期性变化幅度不会随着时间t的变化而变化，也就是让数据尽量呈现出一种接近加法季节性的模式，这样更加方便于我们对数据的预测，不过有时候数据变换对预测结果的影响不会很大，这和幂变换的特点有关。