知识导航
🥳写在前面
本章主要探讨B树的一些性质,不涉及到代码层面的编写,因为B树与红黑树具有一定的等价性,所以理解B树是理解红黑树的前提。后面红黑树章节我们也会提到红黑树与四阶B树具有完全等价性。
一.B树的特点
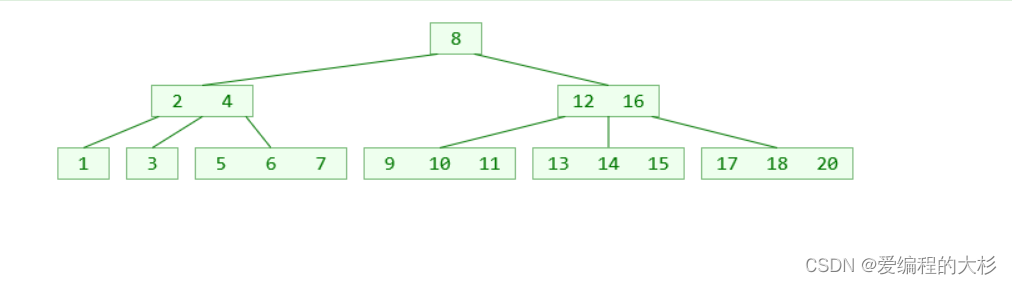
上图中就是一颗B树,通过图片我们不难看出一些端倪:
1.一个B树节点可以存储不止一个元素。
2.一个B树节点可以有超过两个子节点
3.平衡,每个子节点的所有子树高度一致。
当然最直观还是它在存储元素很多的情况下依然保持一个比较矮的高度。
所以不难得出B树是一颗本身就平衡的树,只要符合B树性质那么这颗树就是平衡的,这对于后面理解为什么满足红黑树的性质就一定会平衡有一定的铺垫作用。
二.m阶B树的性质
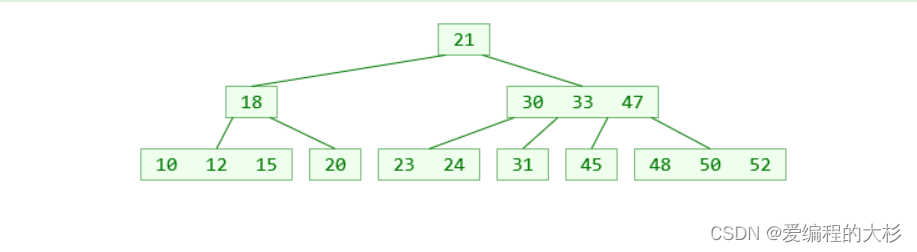 上图就是一颗四阶B树,由特殊到一般可以总结出:
上图就是一颗四阶B树,由特殊到一般可以总结出:
◼ 假设一个节点存储的元素个数为 x
根节点:1 ≤ x ≤ m − 1
非根节点:┌ m/2 ┐ − 1 ≤ x ≤ m − 1
┌ ┐这里是向上取整的意思
如果有子节点,子节点个数 y = x + 1
子节点与元素数目是相差1的关系,所有范围区间加1
✓ 根节点:2 ≤ y ≤ m
✓ 非根节点:┌ m/2 ┐ ≤ y ≤ m
➢ 比如 m = 3,2 ≤ y ≤ 3,因此可以称为(2, 3)树、2-3树
➢ 比如 m = 4,2 ≤ y ≤ 4,因此可以称为(2, 4)树、2-3-4树
➢ 比如 m = 5,3 ≤ y ≤ 5,因此可以称为(3, 5)树
➢ 比如 m = 6,3 ≤ y ≤ 6,因此可以称为(3, 6)树
➢ 比如 m = 7,4 ≤ y ≤ 7,因此可以称为(4, 7)树
三.B树与二叉搜索树
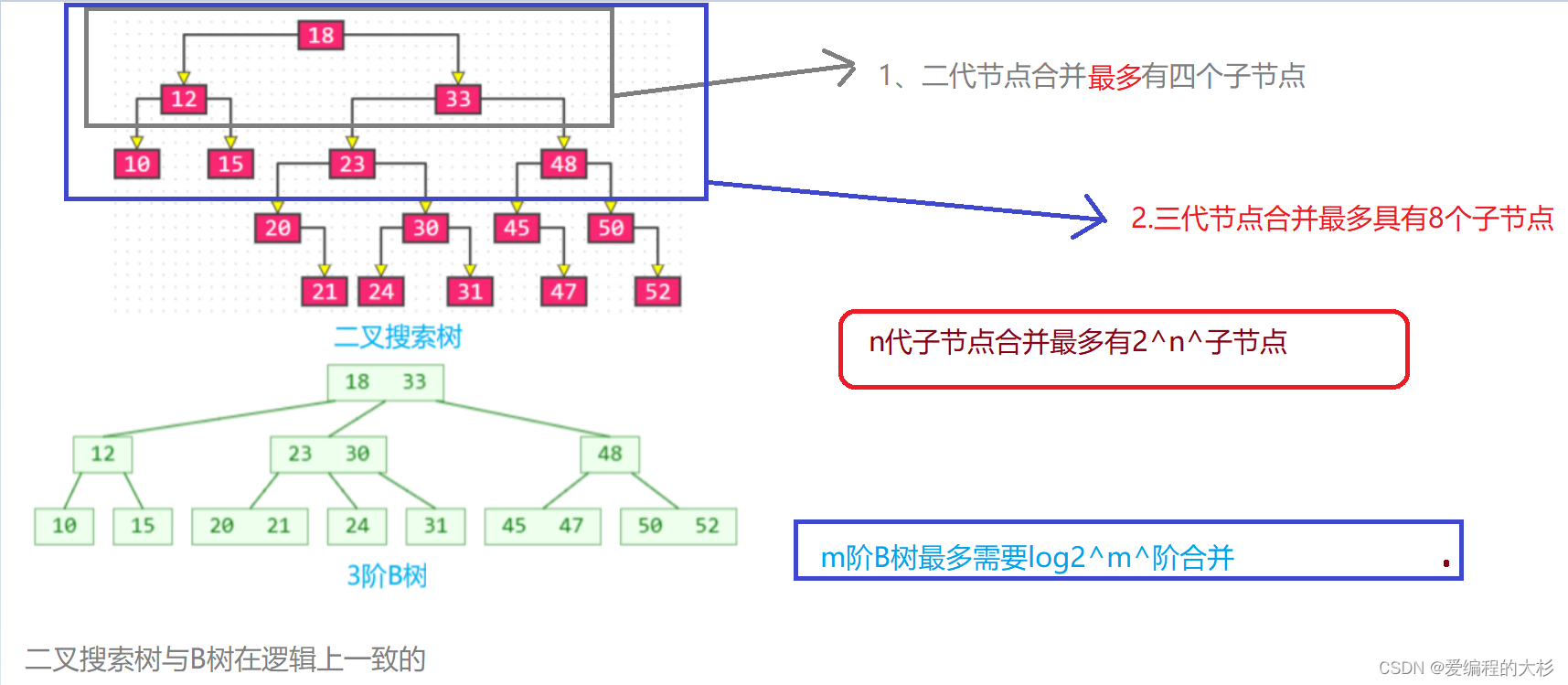
四.B树添加元素
(1)添加导致的上溢及其解决办法
B树添加元素一定是添加在叶子节点
上面我们提到m阶B树每个节点最多有多少个元素,那么一定会有一种情况,就是添加一个元素后达到存储节点的上限—这种情况称之为上溢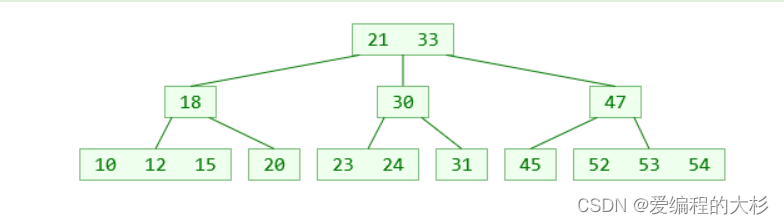 对于上面这棵树如果我们再次添加55,最右面的叶子节点就会超过限制元素个数的上限。
对于上面这棵树如果我们再次添加55,最右面的叶子节点就会超过限制元素个数的上限。
m阶B树节点元素的个数┌m/2┐-1 <X<m-1
◼ 上溢节点的元素个数必然等于 m
◼ 假设上溢节点最中间元素的位置为 k
将 k 位置的元素向上与父节点合并
将 [0, k-1] 和 [k + 1, m - 1] 位置的元素分裂成 2 个子节点
✓ 这 2 个子节点的元素个数,必然都不会低于最低限制(┌ m/2 ┐ − 1)
◼ 一次分裂完毕后,有可能导致父节点上溢,依然按照上述方法解决
最极端的情况,有可能一直分裂到根节点
简言之,就是找出上溢节点的中间元素向上合并然后将原节点该元素左右节点分裂,如果继续上溢则一直向上调整。
五.B树删除元素
(1)删除叶子节点
对于叶子节点中的元素直接删除就可以了
(2)删除非叶子节点
假如需要删除的元素在非叶子节点中
1.先找到前驱或后继元素,覆盖所需删除元素的值
2.再把前驱或后继元素删除(B树节点的前驱或后继一定在叶子节点中)
(归根结底还是删除叶子节点)
(3)删除导致的下溢与解决办法
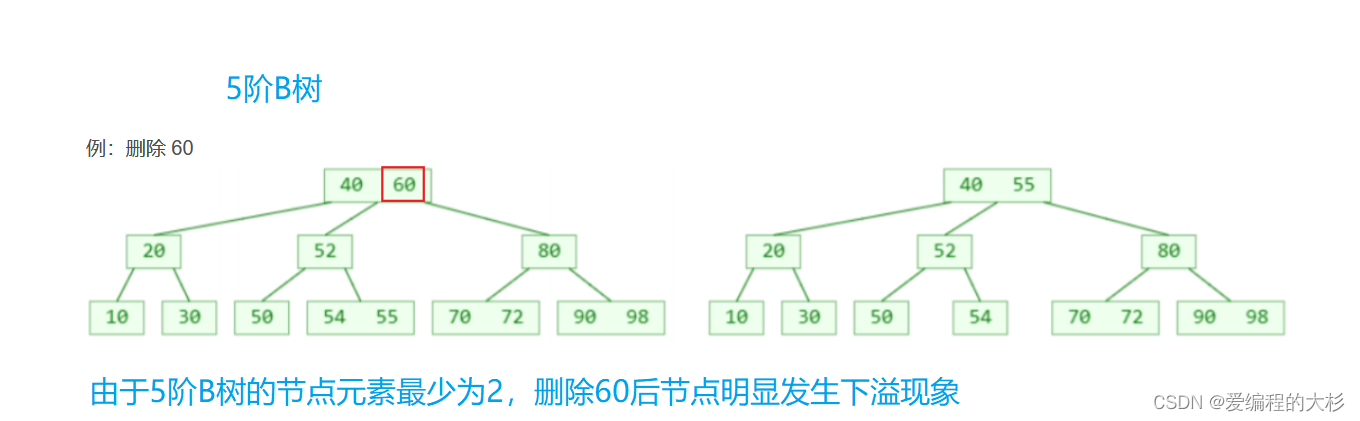
那么如何解决下溢现象
1.向兄弟节点借一个元素(兄弟节点至少有┌ m/2 ┐ 个元素)因为只有这样兄弟节点才不会发生下溢。(这种借的方式我们称之为旋转)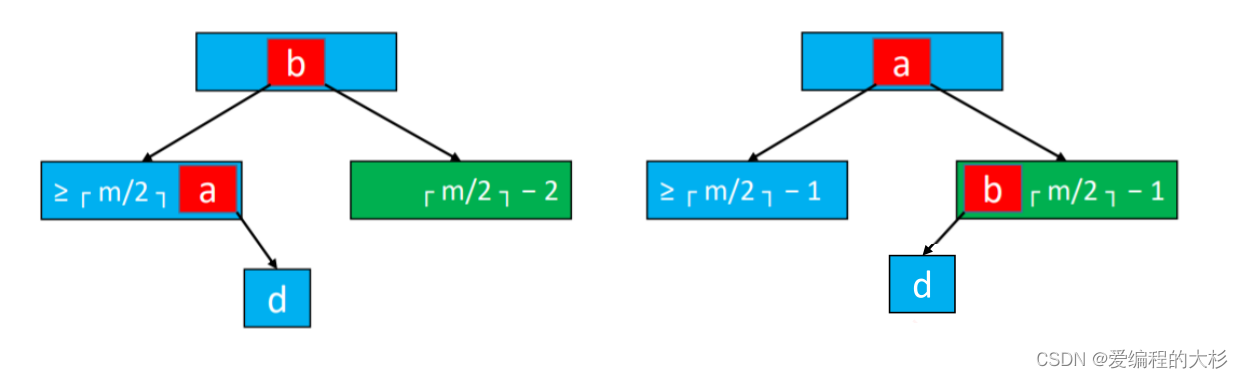 2.如果兄弟节点只有┌ m/2 ┐-1个元素,借出后会继续发生下溢。
2.如果兄弟节点只有┌ m/2 ┐-1个元素,借出后会继续发生下溢。
(1)将父节点的元素 b 挪下来跟左右子节点进行合并
(2)合并后的节点元素个数等于┌ m/2 ┐ + ┌ m/2 ┐ − 2,不超过 m − 1
(3)这个操作可能会导致父节点下溢,依然按照上述方法解决,下溢现象可能会一直往上传播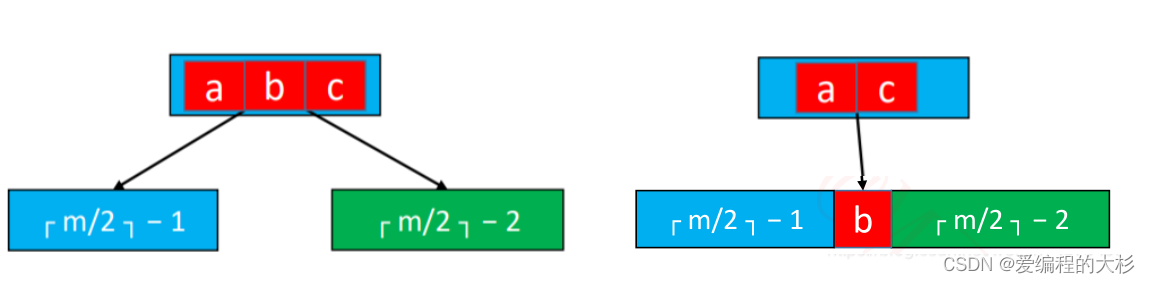
六.四阶B树(对接红黑树)
如果先学习4阶B树(2-3-4树),将能更好地学习理解红黑树
4阶B树的性质
所有节点能存储的元素个数 x :1 ≤ x ≤ 3
所有非叶子节点的子节点个数 y :2 ≤ y ≤ 4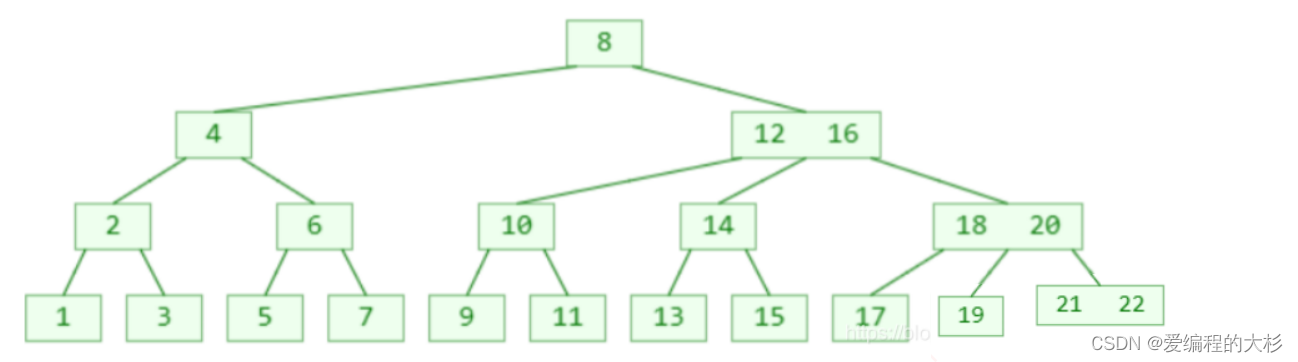

版权归原作者 爱编程的大杉 所有, 如有侵权,请联系我们删除。