信号与系统-离散序列的绘制与卷积（matlab实现）-一个作业的记录

一、实验内容

二、实验目的

1. 熟练知晓离散序列的表示方法并能利用matlab绘制出离散序列的图像
2. 掌握离散序列的基本运算（如加法、乘法、平移、反褶等）并能成功编写对应matlab函数
3. 掌握有限离散序列的卷积运算并能够利用matlab编写卷积函数

三、实验原理

题目一

首先表示出离散信号x（n），对于y(n)可将其拆解为两个信号0.2x(5-n)和0.3x(n)x(n-3)相加，然后分别表示出这两个分量，进行相加。

对于x(5-n)，首先可以利用翻转函数实现信号的翻转得到x(-n)，x(5-n)也即x(-(n-5)),x(-n)图像上方向右平移5个单位得到,可通过将坐标轴向左平移5

个单位达到即让n变为n+5。

得到x(n-3)的方式可类比x(5-n),对x(n)与x(n-3)相乘即可得到第二个分量。

题目二

手写卷积函数的实现，我采用的是对位相乘相加法。

对位相乘相加法原理：

首先将两序列排成两行，其将其各自n最大的序列值对齐（即按右端对齐），然后作乘法运算，但是不要进位，最后将同一列的乘积值相加即得到卷积和结果。

当利用程序实现时，考虑用矩阵存储每一位的乘积，最后进行矩阵的列求和。由于卷积的最终序列长度为length(x)+length(h)-1，所以将此作为矩阵的列数，由对位相乘相加法原理知，矩阵的每一行为分别为h(n)的每一位与x(n)所有相乘的结果，因此矩阵的行数为length(h)。

四、实验结果与分析

（一）离散序列的表示即图像绘制

（1）代码

离散序列图像绘制脚本（Discrete_Signal.m）

clear

n=-2:10;

x=[1:7,6:-1:1];

[x1,n1]=sigfliplr(x,n);

x1=0.2*x1;

[x2,n2]=sigmult(x,n,x,n+3);

x2=0.3*x2;

[y,n]=sigadd(x1,n1+5,x2,n2);

figure

stem(n,y);

title('y(n)');

以下为上述代码中使用的函数的代码：

信号翻转（sigfiplr,m）

function [y,n]=sigfliplr(x,m)

y=fliplr(x);

n=-fliplr(m);

end

信号相乘 （sigmult.m）

function [y,n]=sigmult(x1,n1,x2,n2)

n=min(min(n1),min(n2)):max(max(n1),max(n2));

y1=zeros(1,length(n));

y2=y1;

y1(find(n>=min(n1)&n<=max(n1)))=x1;

y2(find(n>=min(n2)&n<=max(n2)))=x2;

y=y1.*y2;

End

信号相加（sigadd.m）

function [y,n]=sigadd(x1,n1,x2,n2)

n=min(min(n1),min(n2)):max(max(n1),max(n2));

y1=zeros(1,length(n));

y2=y1;

y1(find((n>=min(n1))&(n<=max(n1)==1)))=x1;

y2(find((n>=min(n2))&(n<=max(n2)==1)))=x2;

y=y1+y2;

end         

（2）结果

（二）卷积函数的编写与验证

（1）代码

卷积函数my_conv：

function [y,ny]=my_conv(x,nx,h,nh)

nyb=nx(1)+nh(1);

nye=nx(length(x))+nh(length(h));

ny=nyb:nye;

ly=length(ny);

A=zeros(length(h),ly);

for i=1:length(h)

for j=i:length(x)+i-1

A(i,j)=h(1,i).*x(1,j-i+1);

end

end

y=sum(A,1);

end

验证（Conv_verify）：

clear

nx=0:6;

nh=-3:4;

x=0.5*nx.*(stepseq(0,0,6)-stepseq(6,0,6));

figure

stem(nx,x);

title('x(n)');

h=2*sin(0.5*nh*pi).*(stepseq(-3,-3,4)-stepseq(4,-3,4));

figure

stem(nh,h);

title('h(n)');

[y,ny]=my_conv(x,nx,h,nh);

figure

stem(ny,y);

title('y(n)-myconv');

[yc,nyc]=conv_m(x,nx,h,nh);

figure

stem(nyc,yc);

title('y(n)-standard');

其中，验证使用matlab自带的卷积函数进行对照，此函数包含在conv_m中，如下：

function [y,ny]=conv_m(x,nx,h,nh)

nyb=nx(1)+nh(1);

nye=nx(length(x))+nh(length(h));

ny=[nyb:nye];

y=conv(x,h);

end

（2）结果

X(n)的图像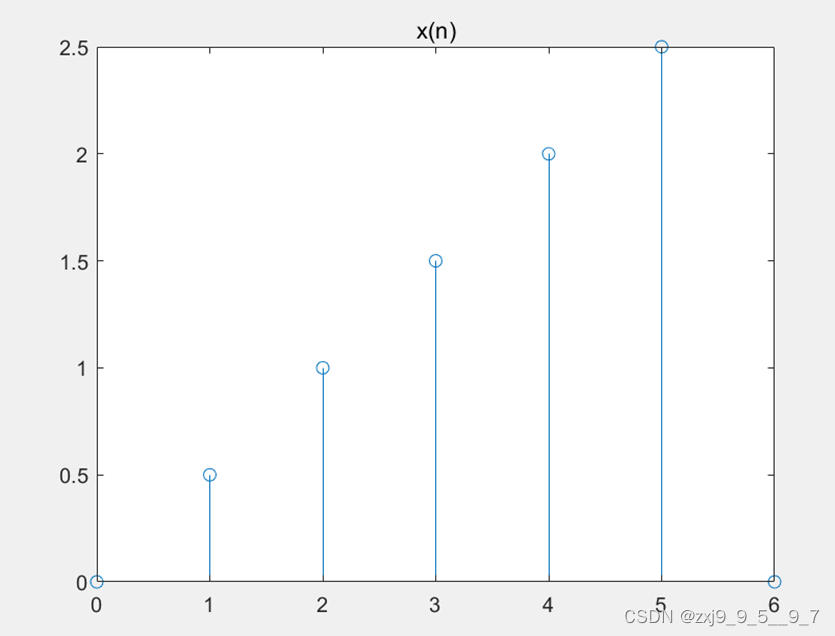

h(n)的图像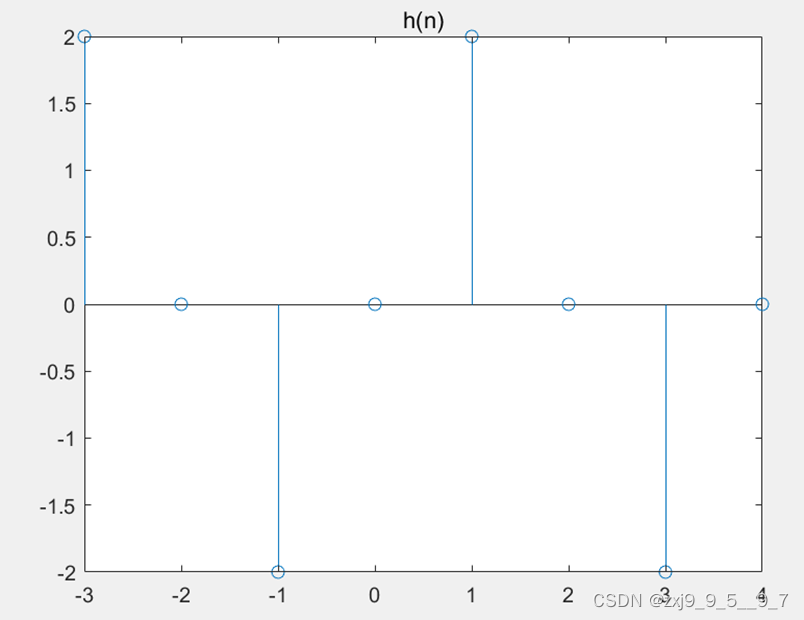

自己编写的卷积函数绘制的y(n)图像

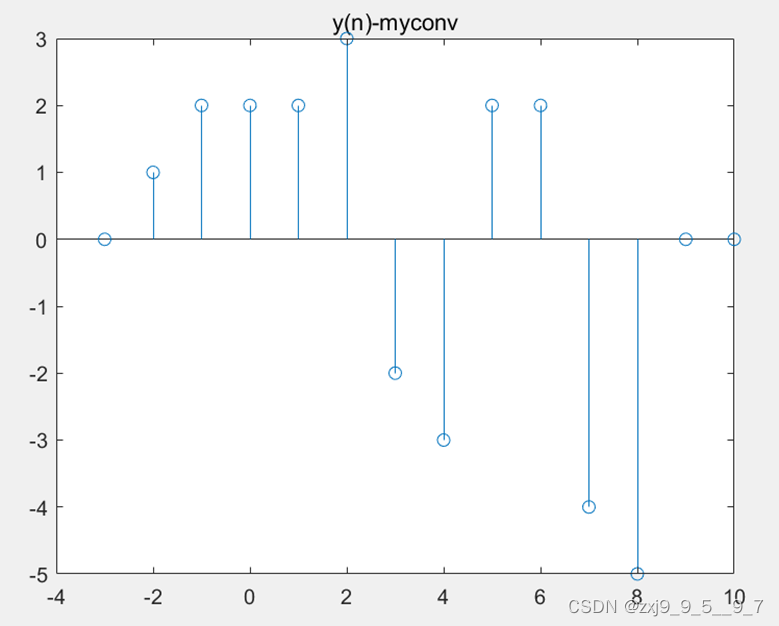采用标准卷积函数绘制的y(n)图像

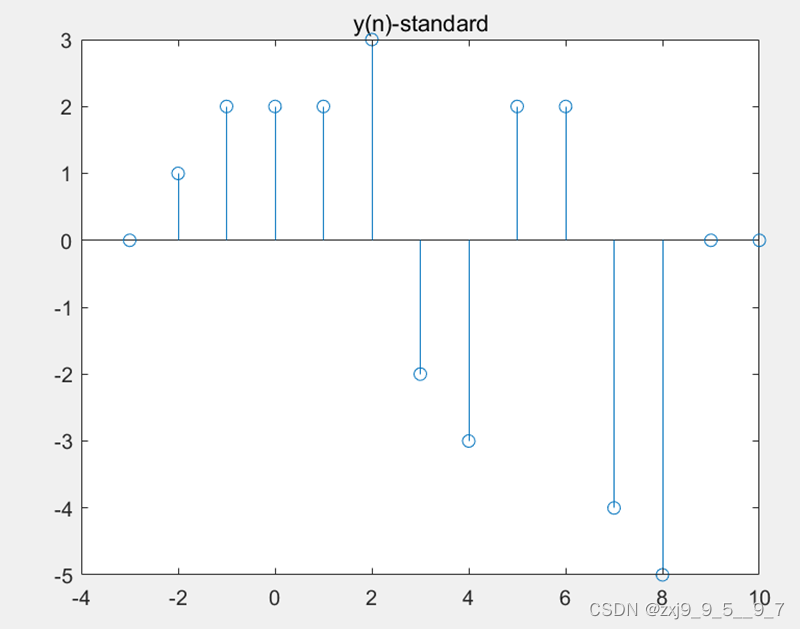
五、总结（实验中遇到的问题、取得的经验、感想等）

此处略