手撕——排序

排序

插入排序

插入排序的前提是未插入时该序列有序。

假如是从小到大排序，插入的数为key，从右向左找小于等于key的值，如果不满足那么原来的向后移动一位进行覆盖，直到满足或者找完进行插入。
重复上面的操作。

voidInsertSort(int* a,int n){int i =0;for(i =0; i < n-1; i++){int end=i;int key = a[end +1];while(end>=0){if(a[end]<= key)break;else
                a[end +1]= a[end];
            end--;}
        a[end +1]= key;}}

时间复杂度O(n*n)
该排序适合接近有序的情况下，在该种情况下时间复杂度接近O(n)

希尔排序

有插入排序演变过来
希尔排序有两个步骤：
1.预排序（尽可能变得有序）
2.插入排序

例：
预排序：把待排序的一组数分为gap组，每一组进行插入排序

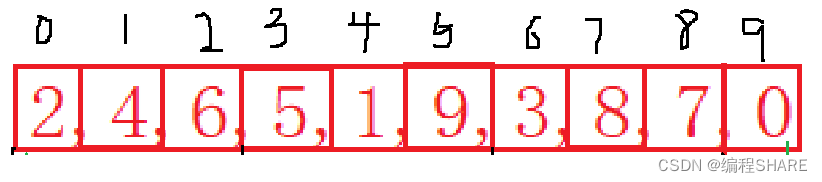
把这10组数分成3组：
第1组：2，5，3，0
第2组：4，1，8
第3组：6，9，7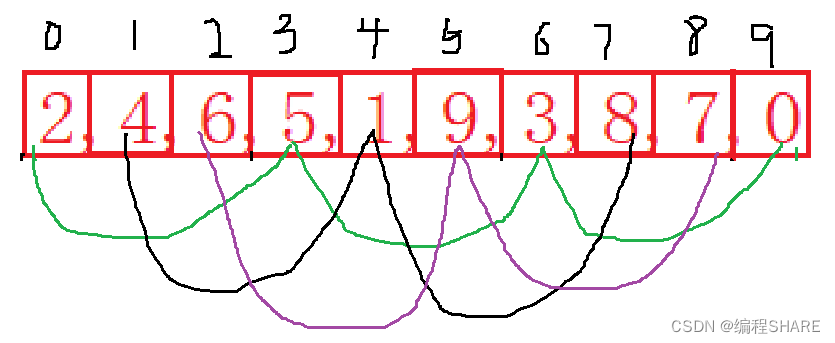

经过预排之后的顺序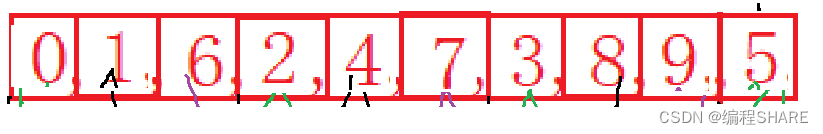

最后全部的进行插入排序，就可以得到有序的序列。
上面例子的代码：

voidShellSort(int* a,int n){int gap =3;for(int i =0; i < n-gap; i++){int end=i;int key = a[end + gap];while(end >=0){if(a[end]<= key)break;else
                a[end + gap]= a[end];
            end -= gap;}
        a[end + gap]= key;}InsertSort(a, n);}

希尔排序动态图

voidShellSort(int* a,int n){int gap = n;while(gap>1){
        gap = gap /2;for(int i =0; i < n-gap; i++){int end = i;int key = a[end + gap];while(end >=0){if(a[end]<= key)break;else
                    a[end + gap]= a[end];
                end -= gap;}
            a[end + gap]= key;}}}

选择排序

选择排序很简单，每一次选出最小的反在前面，选出最大的放在后面。

voidSelectSort(int* a,int n){int min, max;int begin =0, end = n -1;while(begin < end){
        min = max = begin;for(int i = begin; i <= end; i++){if(a[min]> a[i])
                min = i;if(a[max]< a[i])
                max = i;}swap(&a[min],&a[begin]);//注意if(begin == max)
            max = min;swap(&a[max],&a[end]);
        begin++;
        end--;}}

时间复杂度O(N)

堆排序

voidAdjustDwon(int* a,int n,int root){int father = root;int child =2* father +1;while(child <n){if(child<n -1&& a[child]<a[child +1])
            child++;if(a[father]< a[child]){swap(&a[father],&a[child]);
            father = child;
            child =2* father +1;}elsereturn;}}voidHeapSort(int* a,int n){int i =0;for(i =(n -1-1)/2; i >=0; i--){AdjustDwon(a, n, i);}for(i = n -1; i >0; i--){swap(&a[0],&a[i]);AdjustDwon(a, i-1,0);}}

冒泡排序

voidBubbleSort(int* a,int n){int begin =0;int end = n -1;for(int i = begin; i < n-1; i++){for(int j = begin; j < end; j++){if(a[j+1]< a[j])swap(&a[j],&a[j+1]);}
        end--;}}

快速排序

快速排序的基本思路就是：选出一个基值，一般是选取最左边的为基值，然后从右边开始进行遍历，假设是按从小到大的顺序，那么从右边找小的，找到小的之后，在从左边开始找最大的，找到之后两者进行交换。然后继续重复上面的过程，直到左边大于等于右边的时候停止，然后和基数进行交换。
这是一轮

intPartSort1(int* a,int left,int right){int keyi = left;while(left < right){while(left < right && a[keyi]<= a[right])
            right--;while(left < right && a[left]<= a[keyi])
            left++;swap(&a[left],&a[right]);}swap(&a[keyi],&a[right]);
    keyi = left;return keyi;}

坑位法：把基数作为坑位，从右边开始找小（比基数小）的，找到之后填入坑位，该位置变成坑位，然后从左边开始找大，然后再填入坑位，直到找完（左边大于等于右边），把基数填入坑位。

intPartSort2(int* a,int left,int right){int keyi= left;int temp = a[left];while(left < right){while(left<right&&a[right]>= temp){
            right--;}
        a[keyi]= a[right];
        keyi = right;while(left < right && a[left]<= temp){
            left++;}
        a[keyi]= a[left];
        keyi = left;}
    a[keyi]= temp;return keyi;}

前后指针法：
前指针从基数前一个位置开始，后指针从基数位置开始。前指针找小，当找到小的时候，后指针加一，然后前后指针指向的数值进行交换，然后前指针继续找小，直到查找完。

intPartSort3(int* a,int left,int right){int keyi = left;int front = keyi +1;int back = keyi;while(front <= right){if(a[front]<= a[keyi]){
            back++;swap(&a[front],&a[back]);}
        front++;}swap(&a[back],&a[keyi]);
    keyi = back;return keyi;}

上面描述的是一轮排序，每一轮排好之后，都可以确定好排好序之后基数的位置，基数左边是比它小的，右边是比它大的，左边继续排序，右边在继续排序。当还剩一个需要排序的时候就停止排序了。

voidQuickSort(int* a,int left,int right){if(left >= right)return;int keyi = left;//keyi = PartSort1(a, left, right);//keyi = PartSort2(a, left, right);
    keyi =PartSort3(a, left, right);QuickSort(a, left, keyi -1);QuickSort(a, keyi +1, right);}

上面这种排序还不可以，因为他的最坏的时间复杂度为O(N*N)，我们取的基数最好是该组有序数的中间值，但是这个值也不容易在无序中找到，此时我们用3数取中法，把最边的值，最右边的值，还有中间的值，3者进行比较，次大的为基数。为了保证还是上面的方法，我们把基数和最左边的数进行交换。

intThreeIn(int* a,int left,int right){int middle = left +(right - left)/2;if(a[middle]< a[left]){if(a[left]< a[right])return left;elseif(a[middle]< a[right])return right;elsereturn middle;}else{if(a[middle]< a[right])return middle;elseif(a[left]< a[right])return right;elsereturn left;}}voidQuickSort(int* a,int left,int right){if(left >= right)return;int keyi = left;int x =ThreeIn(a, left, right);swap(&a[keyi],&a[x]);//keyi = PartSort1(a, left, right);//keyi = PartSort2(a, left, right);
    keyi =PartSort3(a, left, right);QuickSort(a, left, keyi -1);QuickSort(a, keyi +1, right);}

时间复杂度O(N*logN)

以最左边为基数，为什么从先右边开始呢？

在L与R交换的过程中没有什么可以讨论的，最主要的是相遇的时候和基数进行交换的情况：
1.R遇见L，此时L为最小的或者是基数，交换之后，左小右大。
2.L遇见R:
(1)L与R没有交换
R所处的位置为小，R右边都是大，左边都是小，可以与基值进行交换。
(2)L与R交换
交换过后R还是会继续移动到小的地方，然后和(1)一样。

我们再讨论选左边为基值，还是讨论相遇的情况
1.L遇见R
(1)没有发生交换就相遇了，无法判断相遇时与基值的大小。
(2)L与R交换过后再相遇，此时相遇的为大，不能和基值进行交换。
2.R遇见L
R遇见L说明R与L交换过，此时基值是小的，可以交换。
综上所述:从左边开始并不能完全保证相遇的地方为小的。
非递归形式的快速排序
1.用栈进行实现
用栈储存一组数的上下界，如果从左开始选基数的话，根据栈的特性，我们先储存左边界，再储存右边界。每次排序都从栈中拿出2个数据。当向栈中储存边界的时候要主要边界直接有没有元素。

voidQuickSortNonR1(int* a,int left,int right){

    Stack p;InitStack(&p);StackPush(&p, left);StackPush(&p, right);while(!StackEmpty(&p)){
        right =StackTop(&p);StackPop(&p);
        left =StackTop(&p);StackPop(&p);int keyi =PartSort3(a, left, right);if(keyi +1< right){StackPush(&p, keyi+1);StackPush(&p, right);}if(keyi -1> left){StackPush(&p, left);StackPush(&p, keyi-1);}}StackDestroy(&p);}

2.用队列实现
根据队列的性质，先储存右边界，再储存左边界。后面的过程和栈类似

voidQuickSortNonR2(int* a,int left,int right){
    Queue p;QueueInit(&p);QueuePush(&p, right);QueuePush(&p, left);while(!QueueEmpty(&p)){
        right =QueueFront(&p);QueuePop(&p);
        left=QueueFront(&p);QueuePop(&p);int keyi =PartSort3(a, left, right);if(keyi -1> left){QueuePush(&p, keyi -1);QueuePush(&p, left);}if(keyi +1< right){QueuePush(&p, right);QueuePush(&p, keyi +1);}}QueueDestroy(&p);}

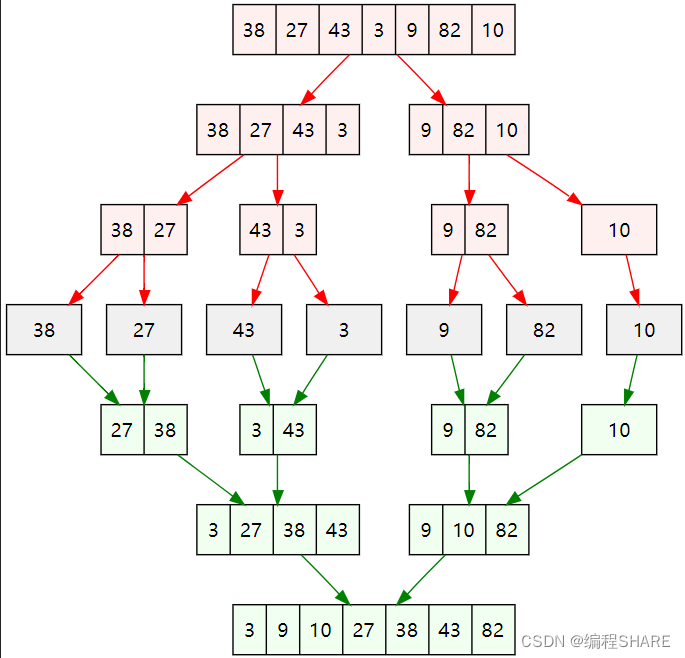
归并排序