机器学习中的七种分类算法

c 机器学习中的 7 种分类算法https://www.projectpro.io/article/7-types-of-classification-algorithms-in-machine-learning/435https://www.projectpro.io/article/7-types-of-classification-algorithms-in-machine-learning/435https://www.projectpro.io/article/7-types-of-classification-algorithms-in-machine-learning/435以上为参考链接。

1 分类任务的类型

1.1 二元分类

主要将数据集分类两类，也意味着输出变量只有两个值。比如将邮件标记为“垃圾邮件”还是“非垃圾邮件”。

1.2 多元分类

数据集分为多个种类，输出变量也有多个值。比如经典的Iris数据集，根据花的花瓣长度、萼片长度、花瓣宽度和萼片宽度，分成三种花。

1.3 多标签分类

一种特殊类型的分类任务，对于数据集中的每个实例具有多个输出变量，也就是说，一个实例可以有多个标签。比如在图像分类中，单个的图像可能包含多个对象，这些对象可以通过算法进行标记，例如公共汽车、红绿灯、斑马线等。

1.4 不平衡分类

不平衡分类是指数据集的实例中具有偏向或者偏态分布的分类问题，也就是一类输入变量的频率高于其他输入变量。比如通过交易数据集中的信用卡检测欺诈交易。通常，此类交易的数量要少得多，因此这会使机器难以学习此类交易。

2 分类算法如何工作

为了解决分类问题，我们使用称为机器学习分类算法的数学模型。他们的任务是找出目标变量如何与输入特征 xi 和输出值 yi 相关联。在数学方面，估计函数 f(xi) 通过将相关特征作为输入来预测输出变量的值。我们可以这样写，

${y}'_{i}= \text{f} \left ( x_{i} \right )$

其中 y'i 表示输出变量的预测响应。

3 数据预处理

在将任何统计算法应用于数据集之前，我们必须彻底了解输入变量和输出变量。在分类问题中，目标总是定性的，但有时，甚至输入值也可以是分类的，例如著名的 Mall Customer Dataset 中客户的性别。由于分类算法是从数学上推导出来的，因此必须将所有变量转换为数值。分类算法工作的第一步是确保变量，无论是输入还是输出，都已正确编码。

4 创建测试集和训练集

处理完数据集后，下一步是将数据集分为两部分：测试数据集和训练数据集。这一步允许使用训练数据集让我们的机器学习输入和输出值之间的模式。另一方面，测试数据集测试模型的准确性，我们将尝试将其放入我们的数据集中。

5 选择模型

一旦我们将数据集拆分为训练和测试，下一个任务就是选择最适合我们问题的模型。为此，我们需要了解流行的分类算法。因此，让我们深入研究不同类型的分类算法池并探索我们的选择。

6 分类算法的类型

以下是您将了解的不同类型分类算法的列表：

朴素贝叶斯分类器
逻辑回归
决策树
随机森林
支持向量机
K-最近邻
K-均值聚类

6.1 朴素贝叶斯分类器

朴素贝叶斯分类器，最简单有效的分类算法之一。它的基础是贝叶斯定理，它描述了如何根据可能与事件相关的条件的先验知识来评估事件的概率。在数学上，这个定理指出——

$\text{P}\left ( Y|X\right )=\frac{P\left ( X|Y\right )P\left ( Y\right )}{P\left ( X\right )}$

其中 P(Y|X) 是事件 Y 的概率，假设 X 已经发生。

P(X) 是事件 X 的概率，

P(Y) 是事件 Y 的概率，

P(X|Y) 是给定 Y 的固定值时事件 X 的可能性。

如果 X 代表一个特征变量，Y 代表一个目标变量，那么贝叶斯分类器会将该标签分配给产生最高概率的特征。为简单起见，考虑一个二分类问题，其中特征变量只能有两个可能的值，Y=1 或 Y=0。然后，如果 Pr(Y=1|X=x0) > 0.5，贝叶斯分类器将预测类别 1，否则预测类别 2。

在不止一个特征的情况下，我们可以使用以下公式来评估概率，

$P\left ( Y|X_{1}=x_{1},X_{2}=x_{2} \right )=\frac{P\left ( X_{1}=x_{1},X_{2} =x_{2}|Y \right )P\left ( Y \right )}{P\left ( X_{1}=x_{1},X_{2}=x_{2} \right )}$

我们假设两个特征 X1 和 X2 是相互独立的。事实上，由于这个假设，“朴素”这个词被附加到贝叶斯的分类器上。

6.1.1 优点

它很简单，实现也很简单。
机器使用这个分类器学习模式所需的时间更少。
它在输入变量具有分类值的情况下表现良好。
它为复杂的现实世界问题提供了良好的结果。
它在多类分类的情况下表现良好。

6.1.2 缺点

它假设特征变量之间的独立性，但情况并非总是如此。
我们经常将其称为坏估计，因此概率并不总是很重要。
如果在训练期间模型不知道任何分类变量并且该变量在测试期间通过，则模型分配 0（零）似然并因此替换称为“零频率”的零概率。可以通过使用平滑程序（例如拉普拉斯估计）来避免这种情况。

6.1.3 应用

垃圾邮件分类： 根据电子邮件的内容识别电子邮件是否为垃圾邮件
实时预测系统： 该模型相对较快，因此可以实时预测目标变量。
情绪分析： 识别产品的反馈并将其分类为“正面”或“负面”。
多类预测： 朴素贝叶斯适用于多类分类问题。

6.2 逻辑回归

该算法类似于贝叶斯分类器，因为它也预测 Y 与输入变量 X 相关联的概率。它使用逻辑函数，

$\large P\left ( X \right )=\frac{e^{\beta _{0}+\beta _{1}X}}{1+e^{\beta _{0}+\beta _{ 1}X}}$

并使用最大似然技术拟合参数 ð??›ƒ0 和 ð??›ƒ1。该技术涉及最大化由下式给出的似然函数

$l\left ( \beta _{0},\beta _{1} \right )=\prod_{l:y_{i}=1}p\left ( x_{i} \right )\prod_{{l} ':y_{{i}'}=1}\left ( 1-p\left ( x_{i} \right ) \right )$

在评估这两个参数后，可以轻松地使用逻辑函数来预测给定输入 xi 的目标变量概率 p(xi)。

对于不止一个特征变量（X1, X2,..., XP），公式可以概括为

$P\left ( X \right )= \frac{e^{\beta _{0}+\beta _{1}X_{1}+\cdots+\beta _{p}X_{p}}}{1+ {e^{\beta _{0}+\beta _{1}X_{1}+\cdots+\beta _{p}X_{p}}}$

6.2.1 优点

这是一个简单的模型，因此训练所需的时间很少。
它可以处理大量的特征。

6.2.2 缺点

虽然它的名字中有回归这个词，但我们只能将它用于分类问题，因为它的范围总是在 0 和 1 之间。
只能用于二分类问题，对多分类问题响应较差

6.2.3 应用

信用评分： 根据年收入、账户余额等一些特征来预测个人的信用（偿还借入贷款的能力）。
预测用户行为： 许多网站使用逻辑回归来预测用户行为并引导他们点击可能感兴趣的链接。
离散选择分析： 逻辑回归是预测人们分类偏好的绝佳选择。这方面的例子可能是买哪辆车、上哪所学校或大学等，这取决于人们的属性和他们可用的各种选择。

6.3 决策树分类算法

该算法涉及根据数据集中的某些特征变量将数据集划分为多个段。这些划分的阈值通常是各自特征变量的平均值或众数（如果它们是数字）。由于树可以表示用于分割数据集的一组分割规则，因此该算法称为决策树。

查看下面的示例以更好地理解它。

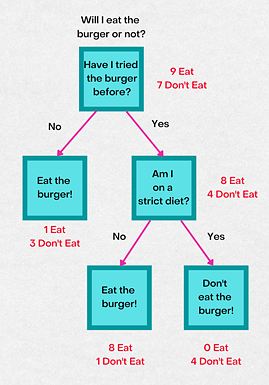
多类分类算法

红色文本表示如何根据输出变量将数据集拆分为多个段。结果是具有最高比例的班级。

现在，很自然要问的问题是该算法使用什么标准来分割数据。有两种广泛使用的度量来测试分割的纯度（如果数据集的片段只有一个类的数据点，则它是纯的）。

第一个是定义的基尼指数

$G= -\sum_{k=1}^{k}p_{mk}\left ( 1-p_{mk} \right )$

测量 N 个类别的总方差。另一种度量是交叉熵，定义为

$D= -\sum_{k=1}^{k}p_{mk}\log \left ( p_{mk} \right )$

在两个等式中，pmk 表示第 m 个片段中属于第 k 个类别的训练变量的比例。

我们根据该特征将数据集拆分为多个段，从而产生熵或基尼指数的最小值。

6.3.1 优点

该算法允许数据的简单表示。因此，更容易向高管解释和解释它。
决策树模仿人类在日常生活中做出决策的方式。
他们顺利处理定性目标变量。
它们有效地处理非线性数据。

6.3.2 缺点

它们可能会创建有时变得无关紧要的复杂树。
与其他算法相比，它们的预测精度水平不同。

6.3.3 应用

情感分析：它用作文本挖掘中的分类算法，以确定客户对产品的情感。
产品选择：公司可以使用决策树来了解哪种产品在推出时会给他们带来更高的利润。

6.4 随机森林分类算法

森林由大量的树木组成。同样，随机森林涉及处理许多决策树。每棵树预测目标变量的概率值。然后我们对产生最终输出的概率进行平均。

我们评估每棵树如下：

通过选择有替换的数据点来创建数据集的第一个样本。
接下来，我们不使用所有输入变量来创建决策树。我们只使用可用的一个子集。
每棵树都被允许长到尽可能大的长度，并且不涉及修剪。

6.4.1 优点

对于大型数据集，它是有效的。
它允许估计输入变量在分类中的重要性。
它比决策树更准确。

6.4.2 缺点

在实施方面更为复杂，因此需要更多时间进行评估。

6.4.3 应用

信用卡违约： 信用卡公司使用随机森林来预测持卡人是否会违约。
股票市场预测： 股票投资者使用它来指示特定股票的趋势并分析其损失和利润。
产品推荐： 可以根据用户的喜好使用它向用户推荐产品。

6.5 支持向量机

该算法利用具有令人兴奋的变化的支持向量分类器，使其适用于评估非线性决策边界。通过使用称为kernels 的特殊函数扩大特征变量空间，这成为可能。该算法考虑的决策边界允许将特征变量标记为目标变量。它用于评估边界的数学函数由下式给出

$f\left ( x \right )= \beta _{0}-\sum_{i \in s }\alpha _{i}K\left ( x,x_{i} \right )$

其中 K 代表核函数。

6.5.1 优点

它使训练数据集变得容易。
当数据是高维时，它表现良好。

6.5.2 缺点

当数据包含噪声元素时，它表现不佳。
它对核函数很敏感，因此必须明智地选择它们。

6.5.3 应用

人脸检测： 用于读取图像（像素数数组）并根据通常的人类特征识别是否包含人脸。
图像分类： SVM 是用于根据图像特征对图像进行分类的图像分类算法之一。
手写字符识别： 我们可以用它来识别手写字符。

6.6 K最近邻分类算法

KNN 算法通过识别给定观察点的 K 个最近邻居来工作。然后它使用 K 个点评估每种类型的目标变量的比例，然后预测具有最高比例的目标变量。例如，考虑以下情况，我们必须将目标值标记为点 X。然后，如果我们在它周围取四个邻居，该模型将预测该点属于粉红色的类。

6.6.1 优点

可以将其应用于任何分布的数据集。
它很容易理解并且非常直观。

6.6.2 缺点

它很容易受到异常值的影响。
它偏向于在数据集中具有更多实例的类。
有时很难找到 K 的最佳数字。

6.6.3 应用

检测异常值： 由于该算法对异常值很敏感，因此可以检测异常值。
识别相似文档： 识别语义相似的文档。

6.7 K-Means聚类算法

K-Means Clustering 是一种将数据集划分为 K 个不重叠的组的聚类算法。该算法的第一步是指定预期的簇数 K。然后，任务是将数据集划分为 K 个簇，以使簇内变化尽可能小。算法过程如下：

为每个输入变量随机分配一个从 1 到 K 的数字。这些是变量的初始聚类标签。
重复该步骤，直到集群分配保持不变：
为 K 个集群中的每一个评估集群质心。
将每个输入变量集分配给质心最近的簇（这里最接近可以用欧氏距离来定义）

总之，该算法最小化输入点与相应聚类质心之间的偏差平方和。将其命名为 K 均值聚类的原因是步骤 2a) 将属于特定聚类的观测值的均值评估为聚类质心。

6.7.1 优点

我们可以将其应用于大型数据集。
实施起来毫不费力。
它保证了定位集群的收敛性。

6.7.2 缺点

它有一个限制，因为必须首先提供 K 的值。
它对异常值很敏感。

6.7.3 应用

添加推荐： 公司可以识别共享金钱消费习惯的客户群，并展示他们更有可能购买的广告。
识别城市中的犯罪区域： 使用 K 均值聚类，我们可以识别更容易发生犯罪案件的区域。
文档分类： 识别写在类似主题上的文档

7 如何决定选择哪种分类算法

下面我们有一个列表，可以帮助您了解应该使用哪些分类算法来解决业务问题。

问题识别： 首先要做的是彻底了解手头的任务。如果是有监督的分类案例，可以使用逻辑回归、随机森林、决策树等算法。另一方面，如果是无监督的分类案例，则应该使用聚类算法。
数据集 的大小：数据集的大小也是您在选择算法时应该考虑的一个参数。由于很少有算法相对较快，因此最好切换到那些算法。如果数据集的大小很小，您可以坚持使用像朴素贝叶斯这样的低偏差/高方差算法。相反，如果数据集很大，特征数量很多，那么你应该使用高偏差/低方差算法，如 KNN、决策树和 SVM。
预测准确度： 模型的准确度是测试分类器好坏的参数。它反映了预测输出值与正确输出值的匹配程度。当然，更高的精度是可取的，但还应检查模型是否过拟合。
训练时间： 有时，像 SVM 和随机森林这样的复杂算法可能会占用大量计算时间。此外，更高的准确性和大数据集无论如何需要更多时间来学习模式。像逻辑回归这样的简单算法更容易实现并节省时间。
**数据集的线性： **输入变量和目标变量之间并不总是存在线性关系。因此，必须分析这种关系并仔细选择算法，因为其中一些仅限于线性数据集。检查线性的最佳方法是拟合线性线或运行逻辑回归或 SVM 并查找残差。较高的误差表明数据是非线性的，需要实施复杂的算法。
特征数量： 有时，数据集可能包含不必要的许多特征，并且并非所有特征都相关。然后可以使用最适合这种情况的 SVM 等算法，或者使用主成分分析来确定哪些特征是重要的。

标签：机器学习分类人工智能

本文转载自: https://blog.csdn.net/qq_40016005/article/details/120598137
版权归原作者 坠星不坠 所有，如有侵权，请联系我们删除。