写在前面
DETR翻译过来就是检测transformer,是Detection Transformers的缩写。这是一个将2017年大火的transformer结构首次引入目标检测领域的模型,是transformer模型步入目标检测领域的开山之作。利用transformer结构的自注意力机制为各个目标编码,依靠其并行性,DETR构造了一个端到端的检测模型,并且避免了以往模型中各种类型的冗余操作,让目标检测问题变得更加简单。
原论文链接
参考视频在这里
对transformer结构的复习在这里:(1)史上最小白之Transformer详解;(2)详解Transformer中Self-Attention以及Multi-Head Attention;
官方源码在这里https://github.com/facebookresearch/detr

文章目录
一、模型特点
DETR模型最大的特点之一就是真正在目标目标检测模型上实现了端到端:DETR没有anchors的生成,在推理阶段最后也没有NMS来过滤掉多余的低质结果,不引入任何人工先验知识,从而简化了模型的pipeline。DETR另一特点就是引入
transformer
结构,通过该结构结合全局信息,考虑目标间的关系并行生成最终的集合预测结果。
二、DETR结构

1. backbone
DETR基础版本的backbone使用torchvision上预训练过的ResNet-50,训练时冻结BN层参数。设输入img维度为(3, H, W),经过backbone后变为(2048,
H
32
{\frac {H} {32}}
32H,
W
32
{\frac {W} {32}}
32W)。此外在后续实验阶段论文还使用了ResNet-101以及改进过的DC5版本,此部分可以看原论文。
2. transformers

在传入encoder前,要对backbone的数据进行一些处理:**(1)由于
transformer
计算开销问题,通过1x1卷积将channel从2048降低到256。(2)转换为序列输入,flatten为(256,
H
32
∗
W
32
{\frac {H}{32}} * {\frac {W}{32}}
32H∗32W),一个向量长为256。** 模块中具体参数可参考DETR官方源码。
(1)encoder
encoder块基本沿用Attention Is all You Need论文中的结构,位置编码使用修正后的位置编码,和ViT一样。每个encoder块结构如上图所示,总encoder部分由N个encoder块堆叠而成,首个块输入为backbone修正后的序列输入,之后块都以上个块的输出为输入,最终输出与输入维度一样。不清楚的
transformer
部分的话可以在本文首对应知识点去复习一下。
(2)decoder
decoder块输入为
object queries
,注意,这是一个可学习的序列输入参数,在论文中维度为(100, 256),序列由100个向量构成,每一个向量长256。如图所示,decoder块大体上符合
transformer
的经典结构,包含两个多头注意力块,这与原始
transformer
不同,没有使用masked多头注意力,原因是这里的是用于处理图像数据的,是非自回归的模型,要求并行输出。其中第一个多头注意力块单纯由
object queries
当作输入和位置编码,第二个多头注意力块则由上层输入以及encoder最终输出作为输入,外加
object queries
给Q位置编码,encoder中使用的修正位置编码给K位置编码,如上图所示。这是一个非常狠心的做法,目的就是为了不断强化模型学习全局信息以及目标见的关系。decoder部分由M个decoder块堆叠而成。decoder部分**最终输出维度与
object queries
相同**。
3. FFNs

FFNs即Feed Forward Networks,用于对transformer结构输出后的数据完成分类+bbox预测任务。两个FFN头共享
transformer
的输出。
- 分类的class FFN使用简单的一层线性层,接受(100, 256)维度输入,输出(100, C + 1)维度的向量,C + 1为“数据集类别数+背景”的个数
- bbox预测的FFN使用三层MLP,接受(100, 256)维度输入,维度变化为(100, 256) >> (100, 512) >> (100, 4)。前两层计算后都接ReLU激活函数,最后一层计算后接sigmoid函数。最终输出维度为(100, 4),代表目标的4个bbox坐标(x, y, w, h)。
4. PS:关于decoder中object queries个数的设置
论文中将object queries的维度设置为100。设置这个数字的原因是:COCO数据集中每张图片中目标个数(正样本)都远低于100,DETR在每张图片上都输出一个元素个数为100的结果集合,集合中包含背景(负样本)。
三、损失函数计算
在训练阶段,DETR有两种损失:(1)二分图匹配阶段的损失,用于确定最优匹配。(2)在最优匹配下的模型损失。
1. 二分图匹配
我们知道DETR每次输出包含N=100个预测目标的集合,由于GT集合元素个数小于N,我们用
ϕ
\phi
ϕ将GT集合元素个数填充至N个。那么预测集合与GT集合总的二分图匹配个数就有
A
N
N
A_{N}^{N}
ANN个,我们所有匹配的集合设为
Σ
N
\Sigma_{N}
ΣN。我们要做的就是找到这个最优的匹配,公式如下图所示。
σ
^
=
a
r
g
m
i
n
σ
∈
Σ
N
∑
i
N
L
m
a
t
c
h
(
y
i
,
y
^
σ
(
i
)
)
\hat{\sigma} = \mathop{arg min}\limits_{\sigma \in \Sigma_{N}} \sum_{i}^{N} L_{match}(y_{i}, \hat{y}_{\sigma(i)})
σ^=σ∈ΣNargmini∑NLmatch(yi,y^σ(i))
σ
^
\hat{\sigma}
σ^即为最优匹配,
y
i
y_{i}
yi与
y
^
σ
(
i
)
\hat{y}_{\sigma(i)}
y^σ(i)分别代表GT值和预测值。
以往的一些研究包括本论文都是使用的匈牙利算法
Hungarian algorithm
来计算最优匹配的。
2. 匹配后损失计算
有了最优的匹配
σ
^
\hat{\sigma}
σ^后,便要计算模型的损失,公式如下。
L
H
u
n
g
a
r
i
a
n
(
y
,
y
^
)
=
∑
i
=
1
N
[
−
l
o
g
p
^
σ
^
(
i
)
(
c
i
)
+
1
{
c
i
≠
ϕ
}
L
b
o
x
(
b
i
,
b
^
σ
^
(
i
)
)
]
L_{Hungarian}(y, \hat{y}) = \sum_{i=1}^{N} [-log \; \hat{p}_{\hat{\sigma}(i)}(c_{i}) + \mathbb{1}_{\{c_{i} \ne \phi\}} L_{box}(b_{i}, \hat{b}_{\hat{\sigma}(i)})]
LHungarian(y,y^)=i=1∑N[−logp^σ^(i)(ci)+1{ci=ϕ}Lbox(bi,b^σ^(i))]
L
b
o
x
(
b
i
,
b
^
σ
^
(
i
)
)
=
λ
i
o
u
L
i
o
u
(
b
i
,
b
^
σ
^
(
i
)
)
+
λ
L
1
∣
∣
b
i
−
b
^
σ
^
(
i
)
∣
∣
1
L_{box}(b_{i}, \hat{b}_{\hat{\sigma}(i)}) = \lambda_{iou}L_{iou}(b_{i}, \hat{b}_{\hat{\sigma}(i)}) + \lambda_{L1} {||b_{i} - \hat{b}_{\hat{\sigma}(i)}||}_{1}
Lbox(bi,b^σ^(i))=λiouLiou(bi,b^σ^(i))+λL1∣∣bi−b^σ^(i)∣∣1
其中
y
i
=
(
c
i
,
b
i
)
y_{i} = (c_{i}, b_{i})
yi=(ci,bi),分别代表GT类别和bbox参数{x, y, w, h};在最优匹配
σ
^
\hat{\sigma}
σ^下,预测的类别分数和bbox参数分别为
p
^
σ
^
(
i
)
(
c
i
)
\hat{p}_{\hat{\sigma}(i)}(c_{i})
p^σ^(i)(ci)和
b
^
σ
^
(
i
)
\hat{b}_{\hat{\sigma}}(i)
b^σ^(i);
λ
i
o
u
\lambda_{iou}
λiou和
λ
L
1
\lambda_{L1}
λL1为超参数用于调节权重。
四、模型表现

上图中第一横栏是在Detectron2上训练3x迭代周期的模型;第二横栏是使用GIoU并且训练9x迭代周期的“精致调教后的Faster R-CNN”模型;第三横栏是DETR。
可以看到,在backbone和参数量相近的情况下,在DETR与精致调教后的Faster R-CNN效果相当(上图中高亮部分),DETR甚至在中大目标检测表现上优于Faster R-CNN,作者将此归功于
transformer
结构;同时,也可以看到DETR在小目标检测表现上败于Faster R-CNN。
五、消融实验

在DETR论文中,作者还针对模型做了许多相关的消融实验。下面简单介绍一些论文中所做的这些消融实验,具体细节还请在原论文中找寻答案。
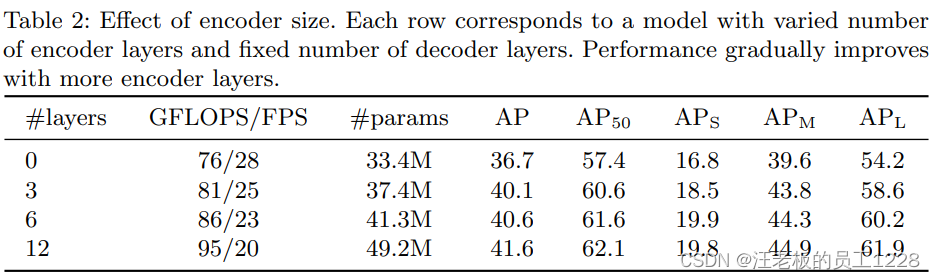
- Encoder层数对模型的影响:encoder对划分开目标实例有举足轻重的作用,所以encoder层数不可以太少,不然会导致最终AP的下降。见下table 2。
- Decoder层数对模型的影响:decoder利用encoder在全局上初步划分开的目标信息,进一步在目标实例某些位置去得到推理结果。Decoder层数太少不足以支撑模型计算目标间的交叉关系,导致模型整体性能下降。见下fig 4与fig 6。
- 内部FFN的重要性:内部FFN其实就是1X1的卷积层。完全移除它们后,模型AP下降了2.3个点。 所以内部FFN很重要。
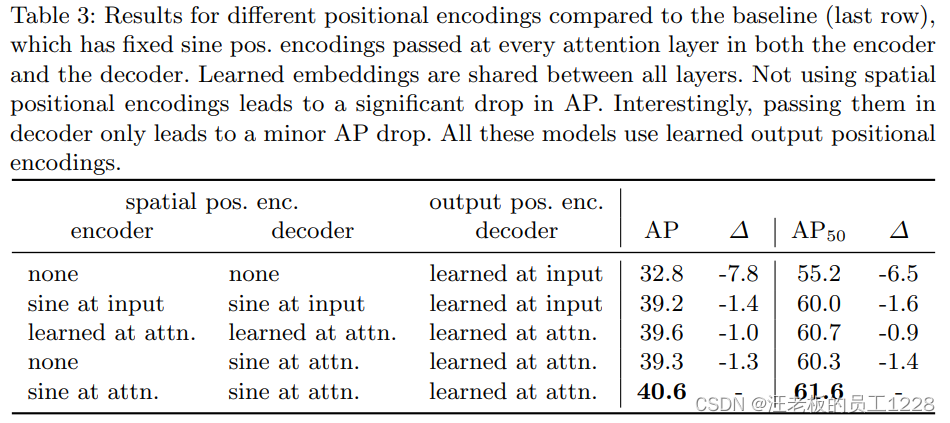
- 位置编码的重要性(两种位置编码):DETR中有两种位置编码,分别为“用于encoder和decoder输入的
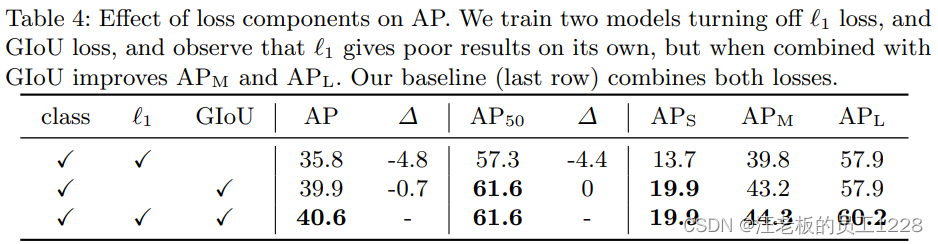
spatial positional encodings”和“用于decoder的可学习的object queries”。论文对于上述两种位置编码应用时机和方式进行了消融实验。见下table 3。 - Loss函数对模型的影响:论文中loss函数的baseline由三部分组成——1. 分类class loss;2. bbox距离L1 loss;3. bbox的GIoU loss。 论文对后两部分做了消融实验,证明baseline的优越性,即三种元素缺一不可。见下table 4。


此外,论文还在附录给出了DETR模型更多更细节的介绍,足足有6页。
版权归原作者 汪老板的员工1228 所有, 如有侵权,请联系我们删除。