医学图像去噪 -----EDCNN

系列文章目录

论文名称：Edge enhancement-based Densely Connected Network with Compound Loss for Low-Dose CT Denoising（基于边缘增强的复合损失密集连接网络在低剂量 CT 去噪中的应用）
论文地址：https://arxiv.org/abs/2011.00139
代码地址：https://github.com/workingcoder/EDCNN
发表时间：2020
应用领域：医学图像去噪
主要模块：包括边缘增强模块（sobel算子）、复合损失函数（MSE+感知损失）。

文章目录

摘要

本文提出了基于边缘增强的稠密连通卷积神经网络EDCNN，在此网络中，我们使用提出的新的可训练Sobel卷积设计了一个边缘增强模块。在此基础上，我们构造了一个具有密集连接的模型来融合提取的边缘信息，实现端到端的图像去噪。此外，在训练模型时，引入了MSE损失和多尺度感知损失相结合的复合损失，解决了模型的过平滑问题，使去噪后的图像质量得到明显改善。与现有的低剂量CT图像去噪算法相比，本文提出的模型在保留细节和抑制噪声方面具有更好的性能。

introduction

低剂量ct巴拉巴拉…近年来，卷积神经网络巴拉巴拉…对于现在有的CNN图像去噪器，该领域的研究人员设计了多种不同结构的模型，包括全连通的神经网络FCN、具有残差连接的卷积编解码网络、或传输-路径以及一些利用3D信息的网络变体等，虽然已经有了很多模型和算法，但低剂量CT图像去噪的任务还没有完全解决。现有的模型也面临着一些问题，如结果过于平滑、边缘丢失、细节信息丢失等。因此，如何提高去噪后的低剂量CT图像质量仍然是研究人员需要解决的关键问题。为了更好地保持图像的细微结构和细节以及降低噪声，本文提出了一种新的CNN模型，基于边缘增强的密集连通卷积神经网络（EDCNN）。总的来说，本文贡献概括如下：

• 设计了一个基于可训练sobel卷积的边缘增强模块，该模块可以在优化过程中自适应地提取边缘特征。
• 构造一个全卷积神经网络（EDCNN），利用传输路径密集连接来融合输入信息和边缘特征信息。
• 在训练阶段引入复合损失，将MSE损失和多尺度感知损失相结合，克服了过度平滑问题。

Realated work

在这一部分中，我们展示了现有的与低剂量CT图像去噪相关的方法，并讨论了它们的实现和性能。

网络结构

编码器-解码器：
编码器-解码器模型采用对称结构设计。利用卷积层构成编码器，对空间信息进行编码。然后，该模型使用相同数量的反卷积层组成解码器，解码器通常使用跳过连接来融合来着编码器的特征映射，如带有残差连接的REDCNN和带有传送路径连接的CPCE等。LDCT图像可以通过整个编码器模型去噪。

全卷积网络：
指整个网络由卷积层组成。低剂量CT图像进行多层卷积运算得到去噪后的输出图像。至于卷积层的配置，不同的模型由不同的思路。有些模型只是使用简单的卷积层，核大小设置为5或3，如11 中的去噪器，如中的模型以不同的扩张速率堆叠卷积层，以增加感受野。此外，这种模型还利用了残差或传输路径连接。
我们提出的EDCNN模型只是设计成FCN结构。

基于GAN的算法：
这类算法包括一个生成器和一个判别器。该生成器被设计成一个降噪网络，可以在测试阶段单独使用。判别器用于区分去噪器的输出和目标大剂量CT图像。他们在一种杜康策略种进行优化，并使用一个交替的训练过程。现有的一些方法：[11]-[13]、[17]用这种结构。随着GAN的进一步发展，研究者们将实现新的模型并进行实验来做进一步探索。

除了这些模型，还有一些算法使用多模型体系结构，它使用级联结构[18]19或并行网络20
我们的论文旨在设计单一模型，高效完成低剂量CT图像降噪任务，因此这类算法在这里不会详细解释。

损失函数

低剂量CT图像去噪是一种图像变化任务，其常用的优化损失函数如下：

Per-pixel loss（逐像素损失）：
低剂量CT图像去噪的目标是得到接近高剂量辐射的结果，因此一个简单的想法是将损失函数直接设置为输出图像与目标图像之间的像素间损失。在这类损失种，常采用均方误差（MSE)损失函数8、9 。L1损失函数也属于这类型。但是，这种损失函数有一个明显的问题。他 不能描述图像中的结构信息，而结构信息在去噪中是很重要的。并且这种类型训练的方法往往输出过平滑的图像。

感知损失：
为了解决图像变换任务中的空间信息依赖性， 21提出了一种新的损失函数-感知损失。它将图像映射到特征空间，并计算该层次上的相似度。关于映射器，经常使用经过训练权值的VGGNet。利用这种损失函数可以较好地保留图像的细节信息，但也存在一些不容忽视的问题，如该方法引入的交叉阴影伪影等。

其他损失：
在基于GAN的去噪算法中，模型在训练过程中使用对抗性损失，受DCGAN23、WGAN24等思想的启发。这些损失函数还可以捕捉图像的结构信息，以生成更逼真的图像。

除了这些类型的损失，研究人员设计了一些特殊形式的损失函数，例如，文献18中的MAP-NN模型提出了包含对抗损失、均方误差(MSE)和边缘不相干损失三个分量的复合损失函数。

虽然有各种损失函数，但它们都是为了参数更高质量的图像而设计的。

模型架构

详细介绍了基于边缘增强的密集连接网络(EDCNN)，包括边缘增强模块、总体模型结构以及用于优化过程的损失函数。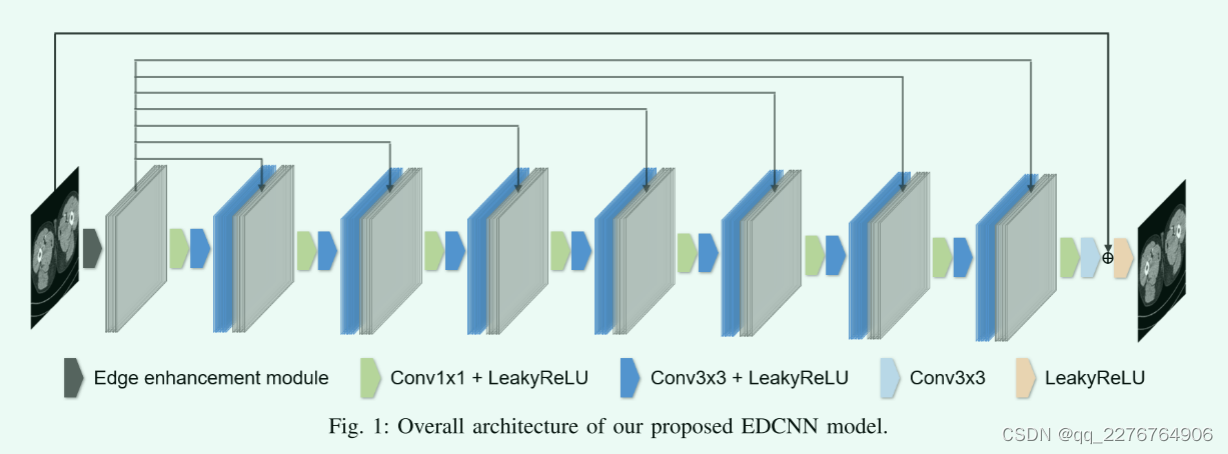

Edge enhancement Module（边缘增强模块）

在描述整个模型的结构之前，本小节首先介绍了直接作用于输入图像的边缘增强模块。 在该模块中，我们设计了可训练的Sobel卷积。 如图所示 2a,与传统的固定值Sobel算子[A 3×3 isotropic gradient operator for image
processing,” Pattern Classification and Scene Analysis]不同，在可训练Sobel算子中定义了一个可学习参数α，我们称之为Sobel因子。 该参数的取值可以在优化训练过程中自适应调整，从而提取出不同强度的边缘信息。 此外，我们定义了四类算子作为一个群（图2a)，包括垂直方向、水平方向和对角线方向。 该模块中可使用多组可训练的Sobel算子。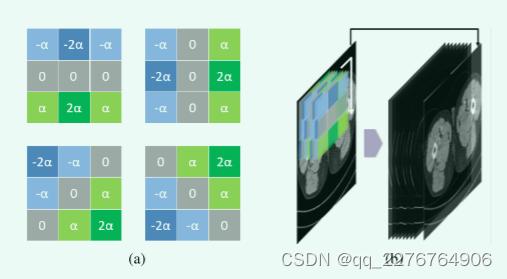

在该模块的流程图中（图2b），1.首先对输入的CT图像使用一定数量（4的倍数）的可训练sobel算子，进行卷积运算得到一组特征图，用于提取边缘信息。2.然后模块将它们与输入的低剂量CT图像在通道维度上叠加在一起，得到该模块的最终输出。该模块的目标是在数据源层面丰富模型的输入信息，强化边信息对模型的作用。

Overall Network Architecture（整体网络架构）

所提出的网络架构如图1所示，称为基于边缘增强的密集连接卷积神经网络（EDCNN）。整个模型由一个边缘增强模块和八个卷积块组成。我们使用的可训练sobel算子的数量是32（四种类型共八组）
至于边缘增强模块之后的模型结构，我们设计的目的是尽量保留过程中的图像细节。受DsenseNet的启发，我们设计了一个密集连接的低剂量CT去噪模型，试图充分利用提取的边缘信息和原始信息。
具体来说，1.如图1中的线所示，我们将边缘增强模块的输出通过skip connection传递给每个卷积块，并在通道上将它们连接起来。2.后面的卷积块的内部结构除了最后一层外完全一样。这些block由11和33卷积组成，卷积滤波器的个数全部设置为32.最后一层3*3卷积了滤波器的个数为1，对应单通道的输出。在每个块中，具有1x1内核的逐点卷积用于融合前一层和边缘增强模块的输出，具有3x3内核的卷积用于向往常一样学习图像中的特征。此外，为了保持输出大小和输入大小相同，模型中的特征图被填充以确保空间大小在前向传播过程中不发生变化。

Compound Loss Function（复合损失函数）

CT图像去噪的最终目标是获得与辐射剂量较高的目标图像相似的输出结果。假设

      I 
     
     
     
       L 
      
     
       D 
      
     
       C 
      
     
       T 
      
     
    
   
     ∈ 
    
    
    
      R 
     
     
     
       1 
      
     
       × 
      
     
       w 
      
     
       × 
      
     
       h 
      
     
    
   
  
    I_{L D C T}\in\mathbb{R}^{1\times w\times h} 
   
  
ILDCT​∈R1×w×h表示一张大小为w*h的LDCT图像， 
 
  
   
    
     
      
       
       
         I 
        
        
        
          N 
         
        
          D 
         
        
          C 
         
        
          T 
         
        
       
      
     
     
      
       
       
         ∈ 
        
        
        
          R 
         
         
         
           1 
          
         
           × 
          
         
           w 
          
         
           × 
          
         
           h 
          
         
        
       
      
     
    
   
  
    \begin{array}{rcl}I_{NDCT}&\in\mathbb{R}^{1\times w\times h}\end{array} 
   
  
INDCT​​∈R1×w×h​表示目标NDCT

图像，去噪任务可以表示为：

     F 
    
   
     ( 
    
    
    
      I 
     
     
     
       L 
      
     
       D 
      
     
       C 
      
     
       T 
      
     
    
   
     ) 
    
   
     = 
    
    
    
      I 
     
     
     
       o 
      
     
       u 
      
     
       t 
      
     
       p 
      
     
       u 
      
     
       t 
      
     
    
   
     ≈ 
    
    
    
      I 
     
     
     
       N 
      
     
       D 
      
     
       C 
      
     
       T 
      
     
    
    
    
   
  
    F(I_{LDCT})=I_{output}\approx I_{NDCT}\quad\text{} 
   
  
F(ILDCT​)=Ioutput​≈INDCT​ (1)

其中F表示降噪方法，

      I 
     
     
     
       o 
      
     
       u 
      
     
       t 
      
     
       p 
      
     
       u 
      
     
       t 
      
     
    
   
  
    I_{output} 
   
  
Ioutput​表示降噪器的输出图像。

为了达到这个目的，以往的方法中普遍采用MSE（Eq.2）作为损失函数，逐像素计算模型输出与目标图像之间的距离。 然而，大量的实验证明，这种损失往往会使输出图像过平滑，增加图像的模糊度。 为了克服这一问题，本文引入了复合损失函数，它融合了MSE损失和多尺度感知损失，如下式所示：

      L 
     
     
     
       m 
      
     
       s 
      
     
       e 
      
     
    
   
     = 
    
    
     
     
       1 
      
     
       N 
      
     
    
    
    
      ∑ 
     
     
     
       i 
      
     
       = 
      
     
       1 
      
     
    
      N 
     
    
    
     
     
       ∥ 
      
     
       F 
      
      
      
        ( 
       
       
       
         x 
        
       
         i 
        
       
      
        , 
       
      
        θ 
       
      
        ) 
       
      
     
       − 
      
      
      
        y 
       
      
        i 
       
      
     
       ∥ 
      
     
    
      2 
     
    
    
    
   
  
    L_{mse}=\dfrac{1}{N}\sum_{i=1}^{N}\left\|F\left(x_{i},\theta\right)-y_{i}\right\|^{2}\quad\quad 
   
  
Lmse​=N1​∑i=1N​∥F(xi​,θ)−yi​∥2 (2)

 
  
   
    
    
      L 
     
     
     
       m 
      
     
       u 
      
     
       l 
      
     
       t 
      
     
       i 
      
     
       − 
      
     
       p 
      
     
    
   
     = 
    
    
     
     
       1 
      
      
      
        N 
       
      
        S 
       
      
     
    
    
    
      ∑ 
     
     
     
       i 
      
     
       = 
      
     
       1 
      
     
    
      N 
     
    
    
    
      ∑ 
     
     
     
       s 
      
     
       = 
      
     
       1 
      
     
    
      S 
     
    
    
     
     
       ∥ 
      
      
      
        ϕ 
       
      
        s 
       
      
      
      
        ( 
       
      
        F 
       
       
       
         ( 
        
        
        
          x 
         
        
          i 
         
        
       
         , 
        
       
         θ 
        
       
         ) 
        
       
      
        , 
       
       
       
         θ 
        
       
         ^ 
        
       
      
        ) 
       
      
     
       − 
      
      
      
        ϕ 
       
      
        s 
       
      
      
      
        ( 
       
       
       
         y 
        
       
         i 
        
       
      
        , 
       
       
       
         θ 
        
       
         ^ 
        
       
      
        ) 
       
      
     
       ∥ 
      
     
    
      2 
     
    
   
  
    L_{multi-p}=\dfrac{1}{NS}\sum\limits_{i=1}^{N}\sum\limits_{s=1}^{S}\left\|\phi_{s}\left(F\left(x_{i},\theta\right),\hat{\theta}\right)-\phi_{s}\left(y_{i},\hat{\theta}\right)\right\|^{2} 
   
  
Lmulti−p​=NS1​i=1∑N​s=1∑S​​ϕs​(F(xi​,θ),θ^)−ϕs​(yi​,θ^)​2 (3)

 
  
   
    
    
      L 
     
     
     
       c 
      
     
       o 
      
     
       m 
      
     
       p 
      
     
       o 
      
     
       u 
      
     
       n 
      
     
       d 
      
     
    
   
     = 
    
    
    
      L 
     
     
     
       m 
      
     
       s 
      
     
       e 
      
     
    
   
     + 
    
    
    
      w 
     
    
      p 
     
    
   
     ⋅ 
    
    
    
      L 
     
     
     
       m 
      
     
       u 
      
     
       l 
      
     
       t 
      
     
       i 
      
     
       − 
      
     
       p 
      
     
    
    
    
   
  
    L_{compound}=L_{mse}+w_{p}\cdot L_{multi-p}\quad\quad 
   
  
Lcompound​=Lmse​+wp​⋅Lmulti−p​ (4)

在这些公式中，我们使用

      x 
     
    
      i 
     
    
   
  
    x_i 
   
  
xi​作为输入， 
 
  
   
    
    
      y 
     
    
      i 
     
    
   
  
    y_i 
   
  
yi​作为目标，N是图像的数量。同上，F

表示参数为

     θ 
    
   
  
    \theta 
   
  
θ的降噪模型。在等式3中的符号 
 
  
   
   
     ϕ 
    
   
  
    \phi 
   
  
ϕ表示模型具有固定的预训练权重 
 
  
   
    
    
      θ 
     
    
      ^ 
     
    
   
  
    \hat{\theta} 
   
  
θ^,用于计算损失。S是尺度的数量。方程4中 
 
  
   
    
    
      w 
     
    
      p 
     
    
   
  
    w_p 
   
  
wp​表示复合损失函数第二部分的权重。

关于感知损失
如图3所示，我们利用ResNet-50作为特征提取器来获得多尺度感知损失。
具体来说，我们丢弃了模型末尾的池化层和全连接，只保留了该模型前面的卷积层。

1. 一开始，我们首先加载在ImageNet数据集上训练的模型权重，然后再训练期间冻结这些权重。
2. 在计算感知损失值时，将去噪输出和目标图像都发送到提取器进行前向传播（图3）。
3. 我们选择ResNet四个阶段后的特征图，在每个阶段图像的空间尺度都会减半，代表不同尺度的特征空间。
4. 然后我们使用MSE来衡量这些特征图的相似度。多尺度感知损失是通过对这些值进行平均得到 将MSE和多尺度感知损失相结合，可以兼顾CT图像的像素间相似性和结构信息。 我们可以调整超参数 w p w_p wp​来平衡两个损耗分量（eq4）。

Experiments And Results(实验结果）

本节解释了用于训练和测试所提出模型的数据，以及实验的配置。然后我们在本节中展示实验结果，评估模型的降噪性能

Dataset

在我们研究的实验中，我们利用了2016年NIH AAPM-Mayo Clinic 低剂量CT大挑战赛的数据集[29]，这是目前低剂量CT图像去噪领域的主流方法所使用的数据集。它包含成对的正常剂量CT(NDCT)图像和合成四分之一剂量CT图像（LDCT)，大小为512*512像素，从10名患者收集。因此用LDCT图像作为模型的输入和NDCT图像作为目标，可以支持监督训练过程。
在数据准备方面，我们在训练前对数据集进行了拆分，使用9名患者的CT图像作为训练集，其余1名患者的图形作为测试集。

Experimental Setup（实验步骤）

该模型是基于Ptorch框架[30]实现的。我们在该模型中对卷积层使用默认的随机初始化，所有边缘增强模块的sobel因子在训练前都初始化为1。此外，复合函数的超参数

      w 
     
    
      p 
     
    
   
  
    w_p 
   
  
wp​设置为0.01。

在训练期间，我们应用了一种crops patch randomly（随机裁剪补丁）的数据增强策略。具体说来，将从一张LDCT图像中随机裁剪出4个大小为6464像素的块，我们使用的输入批次取自32张图像，总共有128块，目标批次的NDCT图像也是如此。在优化过程中，我们使用默认配置的AdamW优化器【32】。我们将学习率设置为0.001，并进行200个epoch的训练以使模型收敛。在测试模型时，由于模型的全卷积结构，对输入图像的大小没有限制。所以我们让训练好的模型使用大小为512512像素的LDCT图像作为输入，直接输出去噪后的结果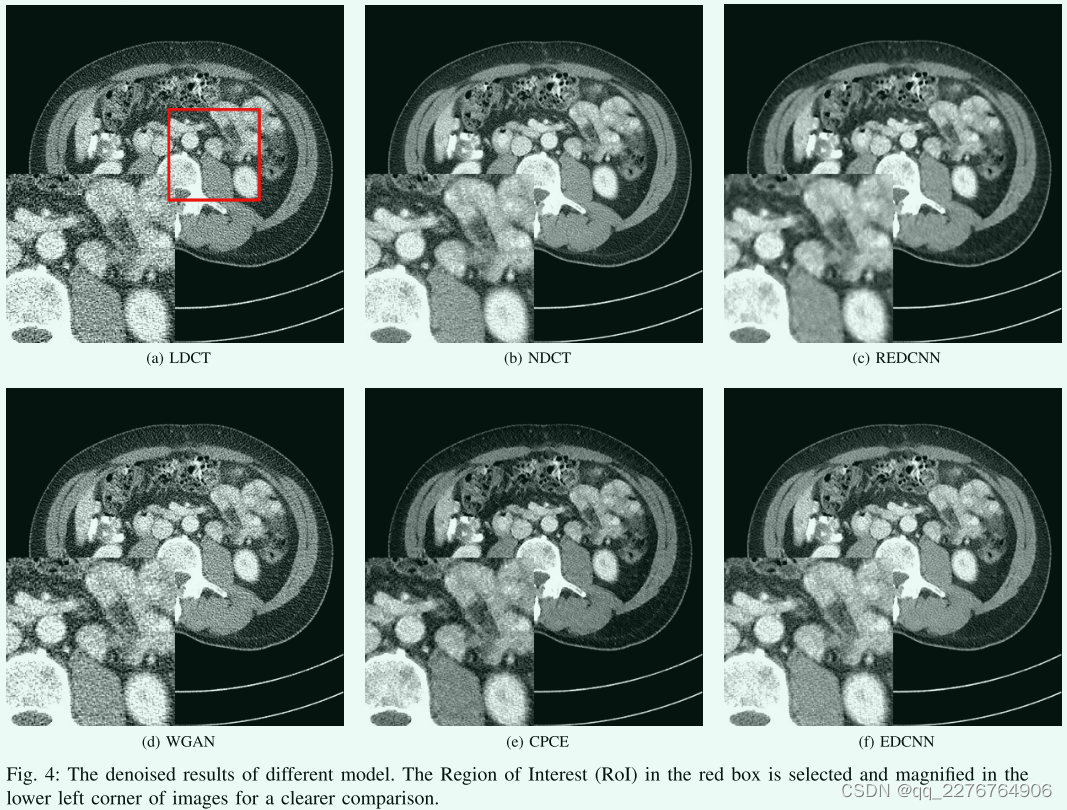

Contrast test（对比试验）

本小结显示了我们模型的降噪结果。为了公平起见我们选择REDCNN 9、WGAN11、和CPCE14进行比较，因为它们的单一模型设计与我们提出的模型相同。这些模型也采用了卷积神经网络的结构，但各有特点。我们重新实现这些模型，在相同的训练集上训练它们。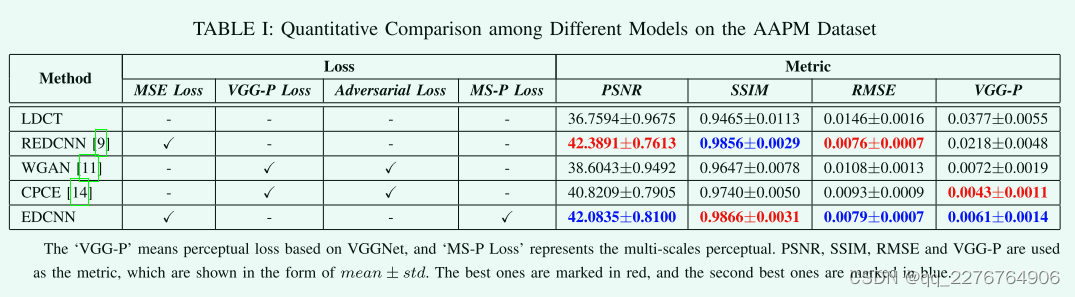

表1的左侧部分。展示了它们使用的损失函数的配置，包括我们的模型。表1的右侧，在降噪任务中，对模型进行定量分析的三个常用标准包括峰值信噪比（PSNR）、结构相似性（SSIM)和均方根误差(RMSE)。此外，我们添加了一个度量，VGG-P，这是基于VGGNet1922的常用感知损失，测量最终卷积层特征空间的距离21。

所有模型都在AAPM Challenge数据集上进行了测试我们计算并统计这些度量的均值和标准差。 通过表1，我们可以发现基于MSE损失的REDCNN在PSNR和RMSE指标上具有最好的性能；利用基于VGGNET的感知损失，WGAN和CPCE对VGG-P有较好的效果； 对于我们提出的EDCNN，它基于复合损耗，在每一个准则上都达到最佳或次优的结果，从而平衡了每像素和结构的性能。由于PSNR和RMSE的计算过程与MSE有直接关系，因此仅用MSE作为损失函数训练的模型可以在这些指标上得到较好的结果。 但这些判据并不能真实反映输出图像的视觉质量，只能作为相对参考。
为了比较去噪结果，如图所示 4.选取一幅结构复杂的CT图像来显示模型的性能。 我们可以注意到LDCT图像（图4A)比NDCT图像（·图）有更多的噪声。 在LDCT图像去噪后，REDCNN的输出（图4C)明显过于光滑虽然它具有最高的PSNR和最低的RMSE，但图像的视觉观感并不好，存在图像模糊和结构细节丢失的问题。 WGAN和CPCE都是基于Wasserstein GAN的感知损失和对抗损失。 图 4D显示的是WGAN去噪后的CT图像，保留了原图像的结构信息，但其对噪声的抑制仍然比较差。 在图放映 4E与图 4F时，CPCE模型和我们的EDCNN具有相当的性能。 它们的输出图像都与目标NDCT图像（图4B)非常相似，保留了CT图像的细微结构。 但从噪声点的细节上，我们还是能注意到它们之间的区别。 EDCNN比CPCE具有更好的降噪性能，这也与表1中的度量值一致。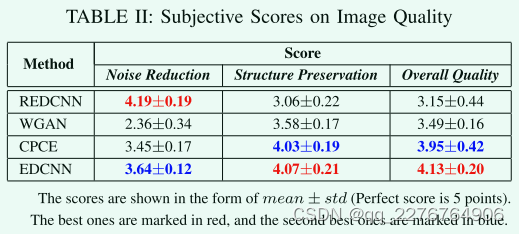

为了获得定量的视觉评价，我们进行了盲读者研究。 具体来说，我们在测试集中选取了20组不同身体部位的模型去噪结果。 每组包括6张CT图像。 以LDCT和NDCT图像为参考，另外四幅图像为上述四种模型的输出，在每组中随机洗牌。 要求读者对去噪后的CT图像从降噪、结构保留和整体质量三个层面进行评分，每项满分5分。 如表2所示，以均值±STD的形式统计主观得分。 REDCNN的降噪性能最好，基于GaN的WGAN和CPCE的结构保持性能较好。 在我们设计的EDCNN模型中，由于复合损失，它既考虑了降噪又考虑了结构的保留。 此外，EDCNN在整体图像质量上得到了很高的分数。

Ablation Study（消融实验）

在这一部分中，我们比较和分析了模型在不同的模型结构和损失函数配置下的性能。并且我们在我们提出的EDCNN模型中讨论了最终设计的有效性。

结构和模块：

为了探索EDCNN模型各组成部分的作用，我们对结构进行了分解实验。
首先，我们设计了一个基本模型（BCNN），从图1所示的结构中去除了密集连接和边缘增强块。
然后，我们依次添加了密集连接（BCNN DC)和边缘增强模块（BCNN DC EM,EDCNN)
为了充分展示模型的潜在能力，所有模型都使用相同的训练策略进行MSE损失训练。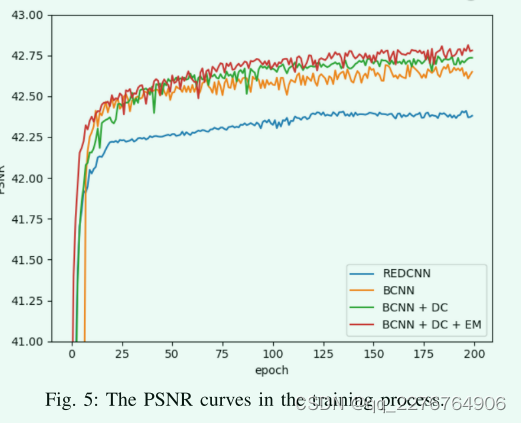

如图5显示PSNR曲线，在每个时期对训练模型的测试集进行测试。我们还添加了REDCNN作为比较。值得注意的是，我们设计的基本模型（BCNN)已经取得了比REDCNN更好的性能。并且通过加入密集连接和边缘增强模块，PSNR的值将不断增加。此外，边缘增强模块加速了模型的收敛过程。在表3中我们可以看到这些模型的PSNR、SSIM、RMSE的值。完整的EDCNN模型在这些指标上有最好的结果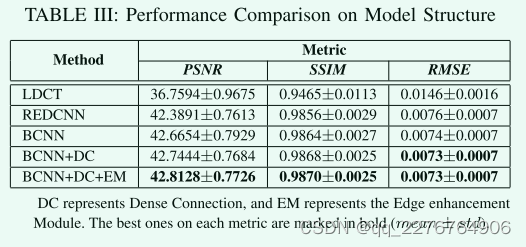

Models of Perceptual Loss（感知损失模型）：

我们的方法中选择用于计算感知损失的模型是RESNet-50.关于感知损失模型，我们将ResNet-50与现有方法常用的VGGNet-19进行了比较。在这个实验中，我们只是通过单一的感知损失来训练EDCNN模型，我们同样利用其最后一个卷积层的feature maps来做比较。

通过感知优化的模型倾向于输出带有某种类似纹理的噪声的图像。仔细观察图6，我们可以发现图6b的噪声颗粒度比图6c大。从视觉上看，图6c更接近于NDCT图像（图6d）。所以我们在我们的感知损失函数中使用了ResNet-50模型，他比VGGNet具有更强的特征提取能力。

Multi-Scales Perceptual Loss（多尺度感知损失）：

在使用perceptual loss时，我们需要决定使用哪一层feature maps。在这里，我们探索多尺度感知损失的不同组合。具体来说，我们利用ResNet-50中四个阶段的输出特征（图3）。设计了四种类型的损失函数，包括S-4、S-43、S-432和S-4321的感知损失，”S“代表阶段，数字表示用于获取特征图的阶段数。损失函数将计算这些阶段提取的特征（eq3）的MSE，并计算它们的平均值以获得最终损失值。图7（a-f)显示了输出图像，我们可以发现随着使用的阶段数增加，去噪结果的”纹理“更接近NDCT图像。因此，我们决定使用ResNet-50模型种四个阶段的输出特征来计算我们方法的感知损失。

Single or Compound Loss（单个损失或者联合损失）

在这个实验中，我们获得了三个分别在单一MSE损失、单一多尺度感知损失和复合损失上训练的EDCN模型。除了他们的损失，它们以同样的方式接受训练。
如图7（g-k）所示，我们可以比较这些去噪CT图像的视觉质量。显然，基于MSE的EDCNN模型（图7h）的结果已经过度平滑，遗漏了太多的细节以供后期诊断。至于图7i和图7j，它们在细节保留方面表现出相似的质量，这进一步验证了多次都感知损失的有效性。同时，我们可以注意到图7j比图7i稍微清晰一些。后者引入了一些可见的伪像。由此可知，基于复合损失的EDCNN具有更好的性能。

Conclusion

总之，本文提出了一种新的基于稠密连通卷积结构的去噪模型，即基于边缘增强的稠密连通网络(EDCNN)。 通过设计的基于可训练Sobel算子的边缘增强模块，该方法能够自适应地获取输入图像更丰富的边缘信息。 此外，我们还引入了复合损失函数，它是MSE损失和多尺度感知损失的加权融合。 利用著名的Mayo数据集，我们进行了大量的实验，与以前的模型相比，我们的方法取得了更好的性能。 在未来，我们计划在EDCNN模型的基础上进一步探索Multimodels结构，并将其推广到其他图像变换任务中。