卷积层的算力评估(MACC和FOPS)

以比较简单的lenet网络模型为例，我们尝试推导主要算子的算力计算公式，并看一下它的各层理论算力要求。

lenet网络结构

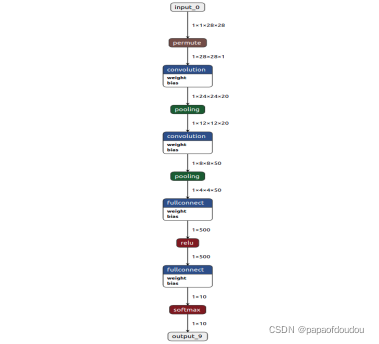
以第二层为例，他的输入尺寸是128281的一张feature map,卷积核为 55*1,stride_h和stride_w均为1， pad_h,pad_w均为0，说明不做padding，输出feature map会缩小。

卷积层的算力评估方法

卷积模型，典型的卷积层计算如下图所示：

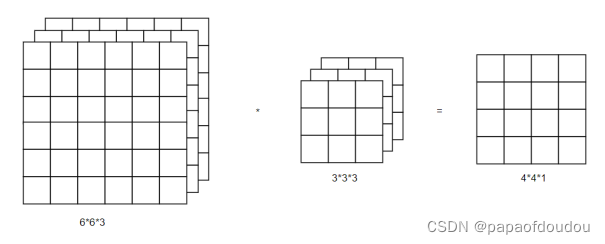
如果输入特征图的宽高分别是,输出特征图的宽高分别是,上下左右填充分别为,水平和垂直方向上的卷积步长为,卷集核宽高分别为,则输出特征图的尺寸计算公式如下：

根据此公式，可以计算得到：

所以，输出feature map的尺寸是24*24。

卷积算力计算

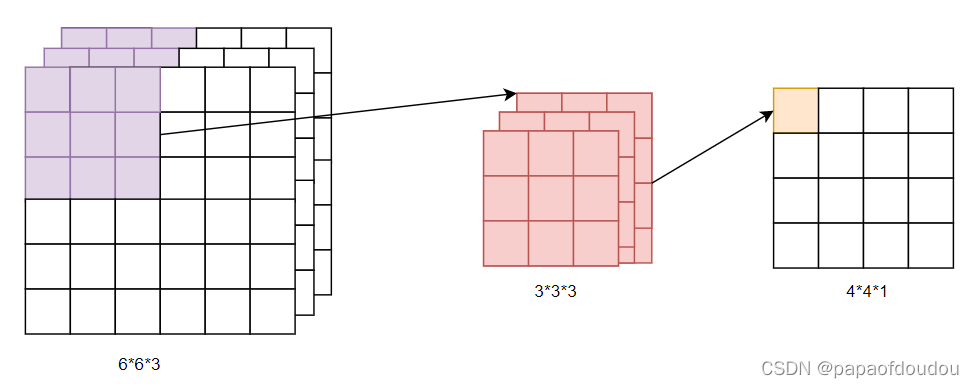
每做一次卷积，生成一个右图中的黄色方块，假设卷积核个数为M，通道数为C，所以卷积总的浮点计算量如下:

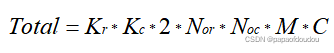
所以，带入数据得到：

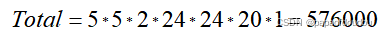
之所以乘以2是因为每次卷积都要分成乘法和加法两次运算，也就是总共需要576000次的浮点数运算。

实际测量

前面我们已经计算出lenet第二层卷积层的理论浮点计算量为28800.pegasus有分析工具也可以对模型进行算力分析，我们用分析工具来验证一下，上面的计算是否正确：

测试命令为：

pegasus measure --model lenet.json

输出结果如下图所示：

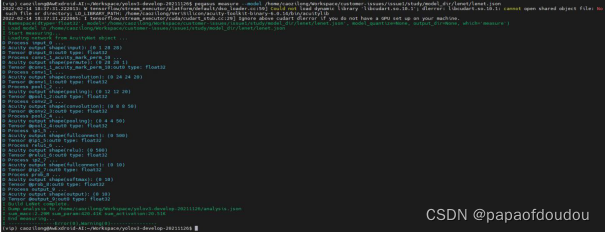
最后输出总的结果为：

sum_macc:2.29M sum_param:420.41K sum_activation:20.51K

同时生成了analysis.json文件，里面列出了各层的算力需求清单，我们直接看第二层conv层面的分析数据，注意看第40行，macc值为：288000，和理论值差着一个因子2，原因何在？

这里直接计算macc表示MAC而不是FOPS了，如果计算FOPS，需要乘以2，计算MACC，就不需要了，应该是这样的吧。

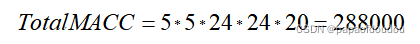
这样就和工具分析一致了。

结束！