使用PyG进行图神经网络的节点分类、链路预测和异常检测

图神经网络(Graph Neural Networks)是一种针对图结构数据(如社交图、网络安全网络或分子表示)设计的机器学习算法。它在过去几年里发展迅速，被用于许多不同的应用程序。在这篇文章中我们将回顾GNN的基础知识，然后使用Pytorch Geometric解决一些常见的主要问题，并讨论一些算法和代码的细节。

常见的图神经网络应用

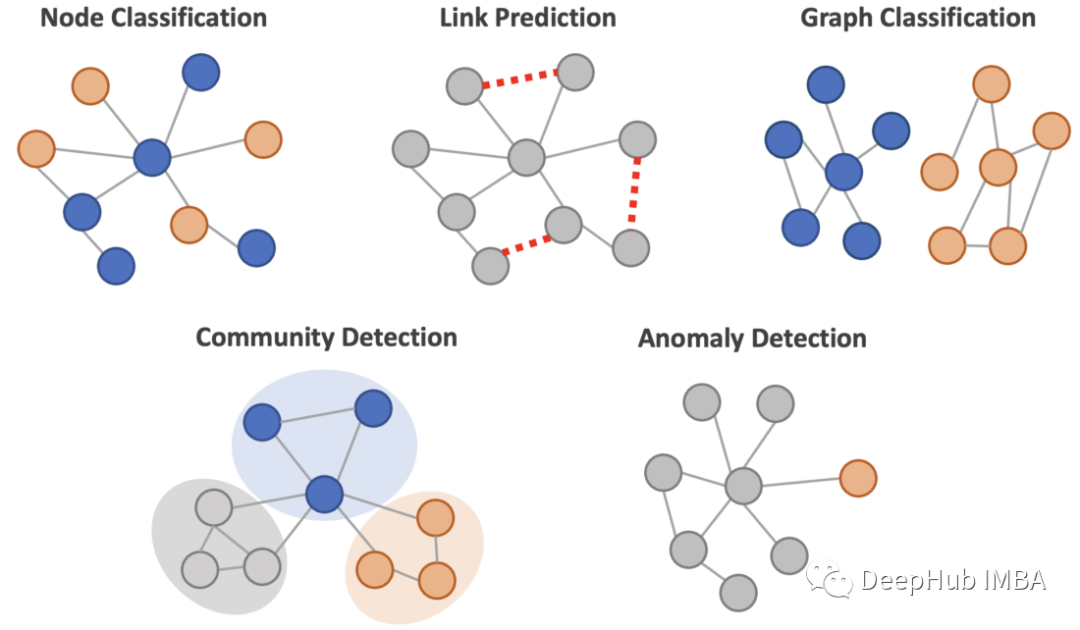
GNN可以用来解决各种与图相关的机器学习问题:

• 节点的分类：预测节点的类别或标签。例如，在网络安全中检测网络中的欺诈实体可能是一个节点分类问题。
• 链接预测：预测节点之间是否存在潜在的链接(边)。例如，社交网络服务根据网络数据建议可能的朋友联系。
• 图分类：将图形本身划分为不同的类别。比如通过观察一个化合物的图结构来确定它是有毒的还是无毒的。
• 社区检测：将节点划分为集群。比如在社交图中寻找不同的社区。
• 异常检测：以无监督的方式在图中查找离群节点。如果没有标签，可以使用这种方法。

在这篇文章中，我们将回顾节点分类、链接预测和异常检测的相关知识和用Pytorch Geometric代码实现这三个算法。

图卷积

图神经网络在过去的几年里发展迅速，并且有许多的变体。在这些GNN变体中图卷积网络可能是最流行和最基本的算法。在本节中我们将对其进行回顾和介绍。

图卷积是一种基于图结构提取/汇总节点信息的有效方法。它是卷积神经网络卷积运算的一个变体，卷积神经网络通常用于解决图像问题。

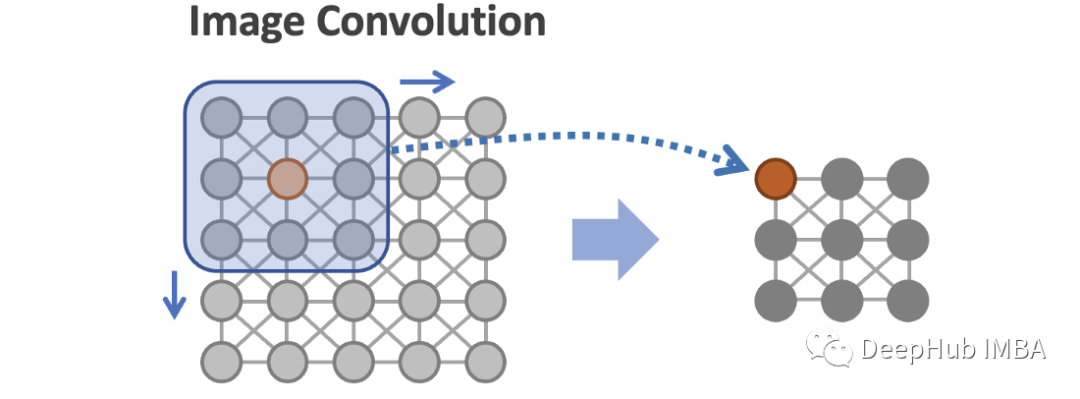
在图像中，像素在网格中按结构排序，卷积操作中的过滤器或卷积核(权重矩阵)以预先确定的步幅在图像上滑动。像素的邻域由过滤器大小决定(下图中过滤器大小为3 x 3，蓝色过滤器中的8个灰色像素为邻域)，过滤器中的加权像素值被聚合为单个值。卷积运算的输出比输入图像的尺寸小，但对输入图像有更高层次的视图，这对预测图像问题很有用，比如图像分类。

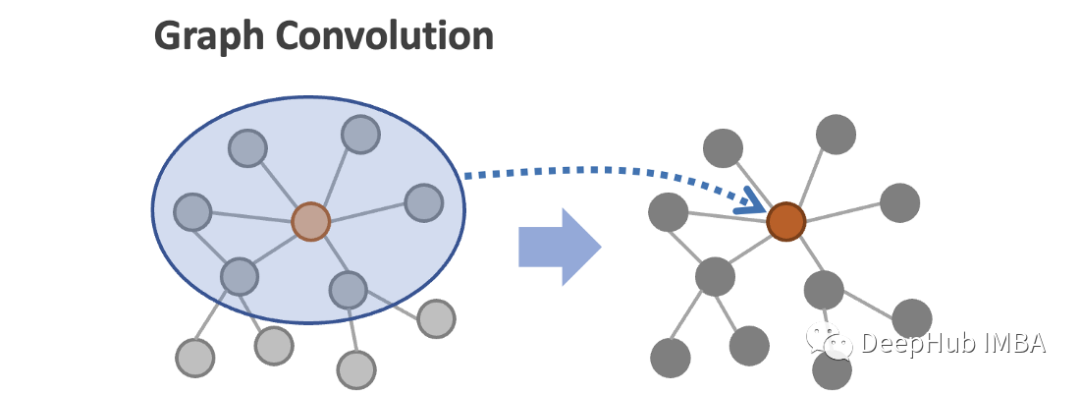
在图中，节点以非结构化的方式排序，节点之间的邻域大小不同。图卷积取给定节点(下图中的红色节点)及其邻居(蓝圈内的灰色节点)的节点特征的平均值，计算更新后的节点表示值。通过这种卷积操作，节点表示捕获局部的图信息。

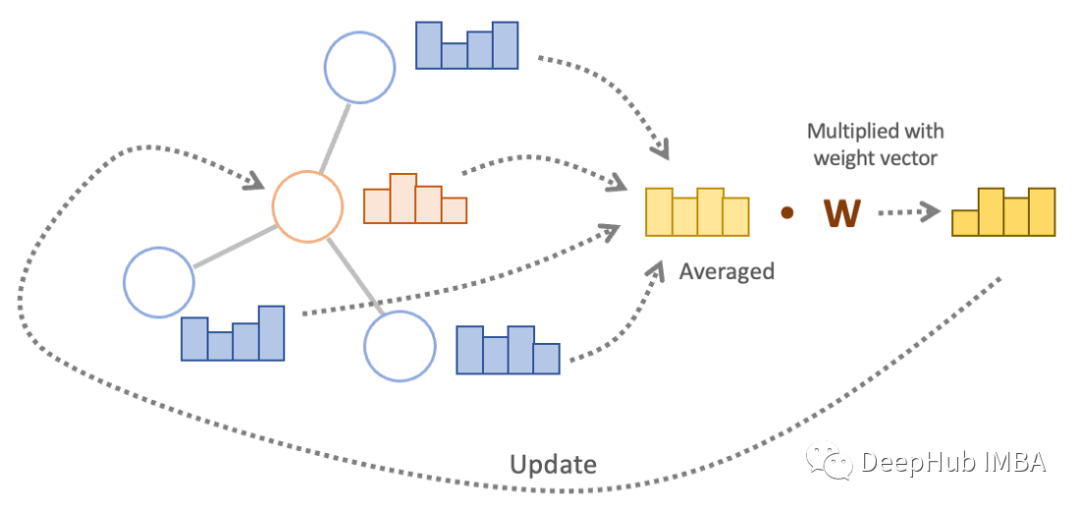
下图显示了更多关于图卷积操作的细节。邻居节点(蓝色)的节点特征和目标节点(红色)的节点特征被平均。然后与权重向量(W)相乘，其输出更新目标节点的节点特征(更新后的节点值也称为节点嵌入)。

对于那些相关的节点，节点特征使用度矩阵的逆进行归一化，然后再聚合而不是简单的平均（原始论文公式8中提出）

这个卷积操作中需要注意的一点是，图卷积的数量决定了节点特征被聚合到每个节点的步数。在下图中，第一个卷积将蓝色节点的特征聚合到橙色节点中，第二个卷积将绿色节点的特征合并到橙色节点中。

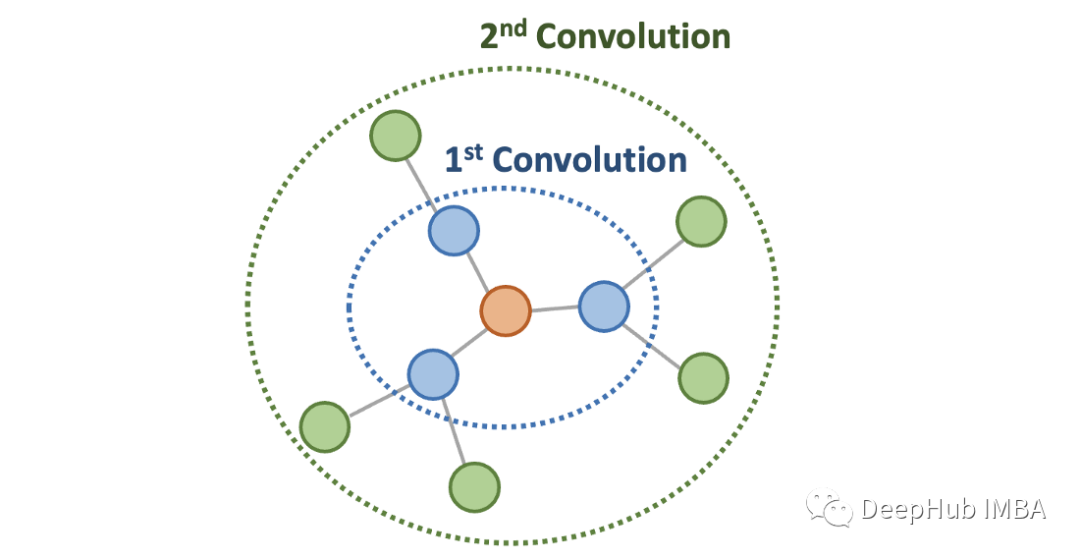
可以看到卷积的数量决定了聚合的节点特征有多远

在接下来的几节中，我们实现GCN。但是在深入研究它们之前，先熟悉一下将要使用的数据集。

Cora - 基准数据集

Cora数据集是一个论文引用网络数据，包含2708篇科学论文。图中的每个节点代表一篇论文，如果一篇论文引用另一篇论文，则有节点间有一条边相连。

我们使用PyG (Pytorch Geometric)来实现GCN, GCN是GNN的流行库之一。Cora数据集也可以使用PyG模块加载:

 from torch_geometric.datasets import Planetoid
 
 dataset = Planetoid(root='/tmp/Cora', name='Cora')
 graph = dataset[0]

Cora数据集来源于Pytorch Geometric的“Automating the Construction of Internet Portals with Machine Learning”论文。

节点特征和边缘信息如下所示。节点特征是 1433 个词向量，表示每个出版物中的词不存在 (0) 或存在 (1)。边在邻接列表中表示。

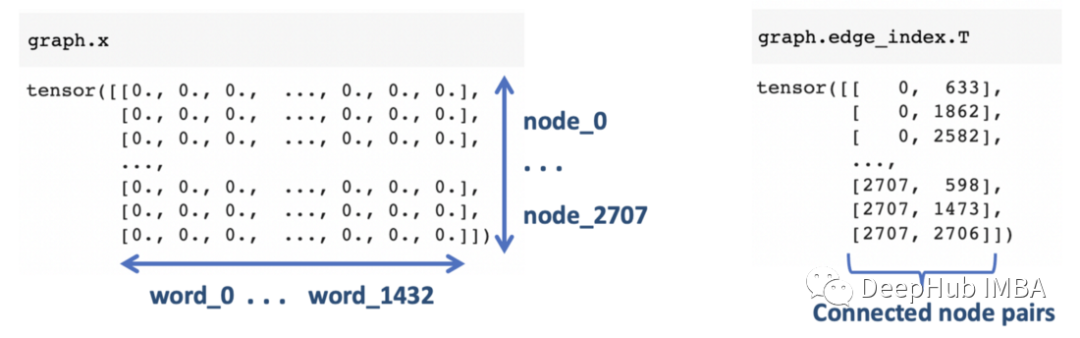
每个节点都是七个类别中的一个，这将就是分类的目标标签

利用NetworkX库可以实现图数据的可视化。节点颜色代表不同的类。

 import random
 from torch_geometric.utils import to_networkx
 import networkx as nx
 
 def convert_to_networkx(graph, n_sample=None):
 
     g = to_networkx(graph, node_attrs=["x"])
     y = graph.y.numpy()
 
     if n_sample is not None:
         sampled_nodes = random.sample(g.nodes, n_sample)
         g = g.subgraph(sampled_nodes)
         y = y[sampled_nodes]
 
     return g, y
 
 
 def plot_graph(g, y):
 
     plt.figure(figsize=(9, 7))
     nx.draw_spring(g, node_size=30, arrows=False, node_color=y)
     plt.show() 
     
     
 g, y = convert_to_networkx(graph, n_sample=1000)
 plot_graph(g, y)

节点分类

对于节点分类问题，可以使用PyG中的RandomNodeSplit模块将节点分为train、valid和test(我替换数据中的原始分割掩码，因为它的训练集太小了)。

 import torch_geometric.transforms as T
 
 split = T.RandomNodeSplit(num_val=0.1, num_test=0.2)
 graph = split(graph)

数据分割标记会被写入到图对象的掩码属性中(参见下图)，而不是图本身。这些掩码用于训练损失计算和模型评估，而图卷积使用整个图数据。

节点分类基线模型(MLP)

在构建GCN之前，只使用节点特征来训练MLP(多层感知器，即前馈神经网络)来创建一个基线性能。该模型忽略节点连接(或图结构)，并试图仅使用词向量对节点标签进行分类。模型类如下所示。它有两个隐藏层(Linear)，带有ReLU激活，后面是一个输出层。

 import torch.nn as nn
 
 class MLP(nn.Module):
     def __init__(self):
         super().__init__()
         self.layers = nn.Sequential(
         nn.Linear(dataset.num_node_features, 64),
         nn.ReLU(),
         nn.Linear(64, 32),
         nn.ReLU(),
         nn.Linear(32, dataset.num_classes)
         )
 
     def forward(self, data):
         x = data.x  # only using node features (x)
         output = self.layers(x)
         return output

我们用一个普通的Pytorch训练/验证流程来定义训练和评估函数。

 def train_node_classifier(model, graph, optimizer, criterion, n_epochs=200):
 
     for epoch in range(1, n_epochs + 1):
         model.train()
         optimizer.zero_grad()
         out = model(graph)
         loss = criterion(out[graph.train_mask], graph.y[graph.train_mask])
         loss.backward()
         optimizer.step()
 
         pred = out.argmax(dim=1)
         acc = eval_node_classifier(model, graph, graph.val_mask)
 
         if epoch % 10 == 0:
             print(f'Epoch: {epoch:03d}, Train Loss: {loss:.3f}, Val Acc: {acc:.3f}')
 
     return model
 
 
 def eval_node_classifier(model, graph, mask):
 
     model.eval()
     pred = model(graph).argmax(dim=1)
     correct = (pred[mask] == graph.y[mask]).sum()
     acc = int(correct) / int(mask.sum())
 
     return acc
   
   
 mlp = MLP().to(device)
 optimizer_mlp = torch.optim.Adam(mlp.parameters(), lr=0.01, weight_decay=5e-4)
 criterion = nn.CrossEntropyLoss()
 mlp = train_node_classifier(mlp, graph, optimizer_mlp, criterion, n_epochs=150)
 
 test_acc = eval_node_classifier(mlp, graph, graph.test_mask)
 print(f'Test Acc: {test_acc:.3f}')

该模型的测试精度为73.2%。

GCN进行节点分类

接下来，我们将对GCN进行训练并将其性能与MLP进行比较。这里使用的是一个非常简单的模型，有两个图卷积层和它们之间的ReLU激活。此设置与论文原文相同(公式9)。

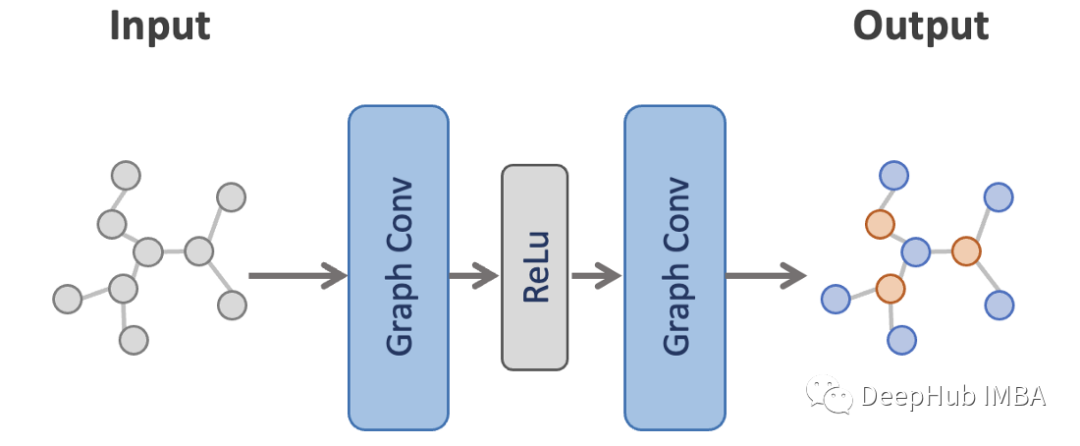
 from torch_geometric.nn import GCNConv
 import torch.nn.functional as F
 
 class GCN(torch.nn.Module):
     def __init__(self):
         super().__init__()
         self.conv1 = GCNConv(dataset.num_node_features, 16)
         self.conv2 = GCNConv(16, dataset.num_classes)
 
     def forward(self, data):
         x, edge_index = data.x, data.edge_index
 
         x = self.conv1(x, edge_index)
         x = F.relu(x)
         output = self.conv2(x, edge_index)
 
         return output
     
     
 gcn = GCN().to(device)
 optimizer_gcn = torch.optim.Adam(gcn.parameters(), lr=0.01, weight_decay=5e-4)
 criterion = nn.CrossEntropyLoss()
 gcn = train_node_classifier(gcn, graph, optimizer_gcn, criterion)
 
 test_acc = eval_node_classifier(gcn, graph, graph.test_mask)
 print(f'Test Acc: {test_acc:.3f}')

该模型的测试集准确度为88.0%。从MLP中获得了大约15%的精度提高。

链接预测

链接预测比节点分类更复杂，因为我们需要使用节点嵌入对边缘进行预测。预测步骤大致如下:

• 编码器通过处理具有两个卷积层的图来创建节点嵌入。
• 在原始图上随机添加负链接。这使得模型任务变为对原始边的正链接和新增边的负链接进行二元分类。
• 解码器使用节点嵌入对所有边(包括负链接)进行链接预测(二元分类)。它从每条边上的一对节点计算节点嵌入的点积。然后聚合整个嵌入维度的值，并在每条边上创建一个表示边存在概率的值。

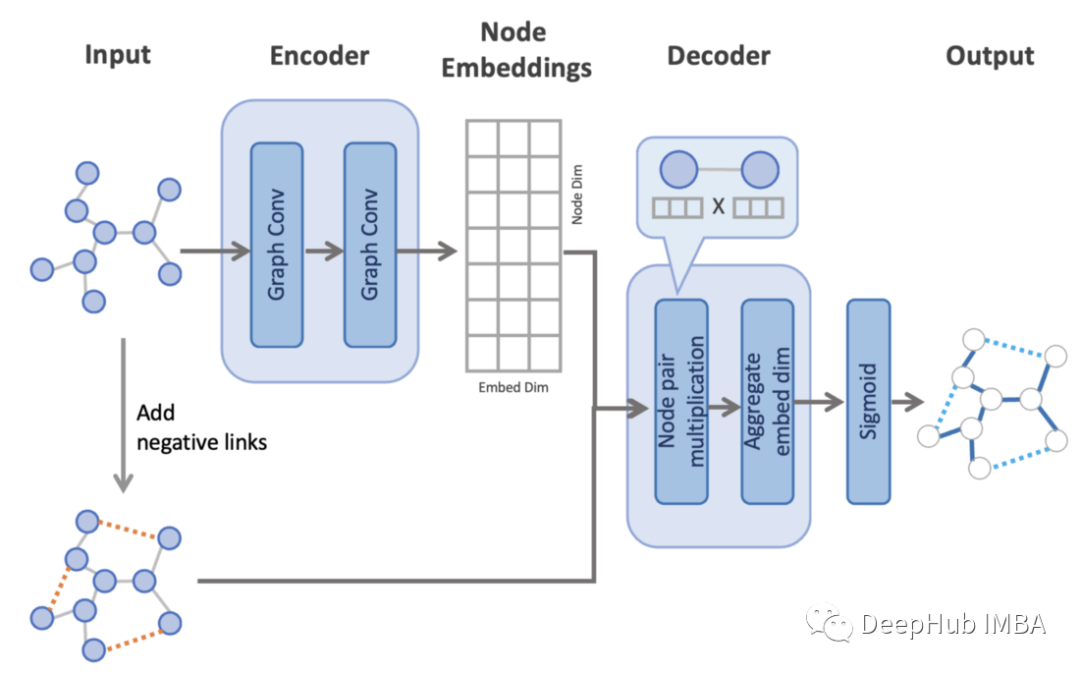
该模型结构来源于变分图自动编码器中原始的链接预测实现。代码改编自PyG repo中的代码示例，并基于Graph Auto-Encoders实现

 from sklearn.metrics import roc_auc_score
 from torch_geometric.utils import negative_sampling
 
 
 class Net(torch.nn.Module):
     def __init__(self, in_channels, hidden_channels, out_channels):
         super().__init__()
         self.conv1 = GCNConv(in_channels, hidden_channels)
         self.conv2 = GCNConv(hidden_channels, out_channels)
 
     def encode(self, x, edge_index):
         x = self.conv1(x, edge_index).relu()
         return self.conv2(x, edge_index)
 
     def decode(self, z, edge_label_index):
         return (z[edge_label_index[0]] * z[edge_label_index[1]]).sum(
             dim=-1
         )  # product of a pair of nodes on each edge
 
     def decode_all(self, z):
         prob_adj = z @ z.t()
         return (prob_adj > 0).nonzero(as_tuple=False).t()
     
 
 def train_link_predictor(
     model, train_data, val_data, optimizer, criterion, n_epochs=100
 ):
 
     for epoch in range(1, n_epochs + 1):
 
         model.train()
         optimizer.zero_grad()
         z = model.encode(train_data.x, train_data.edge_index)
 
         # sampling training negatives for every training epoch
         neg_edge_index = negative_sampling(
             edge_index=train_data.edge_index, num_nodes=train_data.num_nodes,
             num_neg_samples=train_data.edge_label_index.size(1), method='sparse')
 
         edge_label_index = torch.cat(
             [train_data.edge_label_index, neg_edge_index],
             dim=-1,
         )
         edge_label = torch.cat([
             train_data.edge_label,
             train_data.edge_label.new_zeros(neg_edge_index.size(1))
         ], dim=0)
 
         out = model.decode(z, edge_label_index).view(-1)
         loss = criterion(out, edge_label)
         loss.backward()
         optimizer.step()
 
         val_auc = eval_link_predictor(model, val_data)
 
         if epoch % 10 == 0:
             print(f"Epoch: {epoch:03d}, Train Loss: {loss:.3f}, Val AUC: {val_auc:.3f}")
 
     return model
 
 
 @torch.no_grad()
 def eval_link_predictor(model, data):
 
     model.eval()
     z = model.encode(data.x, data.edge_index)
     out = model.decode(z, data.edge_label_index).view(-1).sigmoid()
 
     return roc_auc_score(data.edge_label.cpu().numpy(), out.cpu().numpy())

对于这个链接预测任务，我们希望将链接/边随机分割为训练数据、有效数据和测试数据。我们可以使用PyG的RandomLinkSplit模块来做到这一点。

 import torch_geometric.transforms as T
 
 split = T.RandomLinkSplit(
     num_val=0.05,
     num_test=0.1,
     is_undirected=True,
     add_negative_train_samples=False,
     neg_sampling_ratio=1.0,
 )
 train_data, val_data, test_data = split(graph)

输出数据如下所示。

这个输出数据有以下3点需要注意：

1、在edge_index上执行分割，这样训练和验证分割不包括来自验证和测试分割的边(即只有来自训练分割的边)，而测试分割不包括来自测试分割的边。这是因为编码器使用edge_index和x来创建节点嵌入，这种方式确保了在对验证/测试数据进行预测时，节点嵌入上没有目标泄漏。

2、向每个分割数据添加两个新属性(edge_label和edge_label_index)。它们是与每次分割相对应的边标签和边索引。Edge_label_index将用于解码器进行预测，edge_label将用于模型评估。

3、向val_data和test_data添加与正链接相同数量的负链接(neg_sampling_ratio=1.0)。它们被添加到edge_label和edge_label_index属性中，但没有添加到edge_index中，因为我们不希望在编码器(或节点嵌入创建)上使用负链接。我们没有向这里的训练集添加负链接(设置add_negative_train_samples=False)，因为会在上面的train_link_predictor的训练循环中添加它们。训练过程中的这种随机化应该会使模型更健壮。

下图总结了如何对编码器和解码器执行边缘分割(每个阶段使用彩色边缘)。

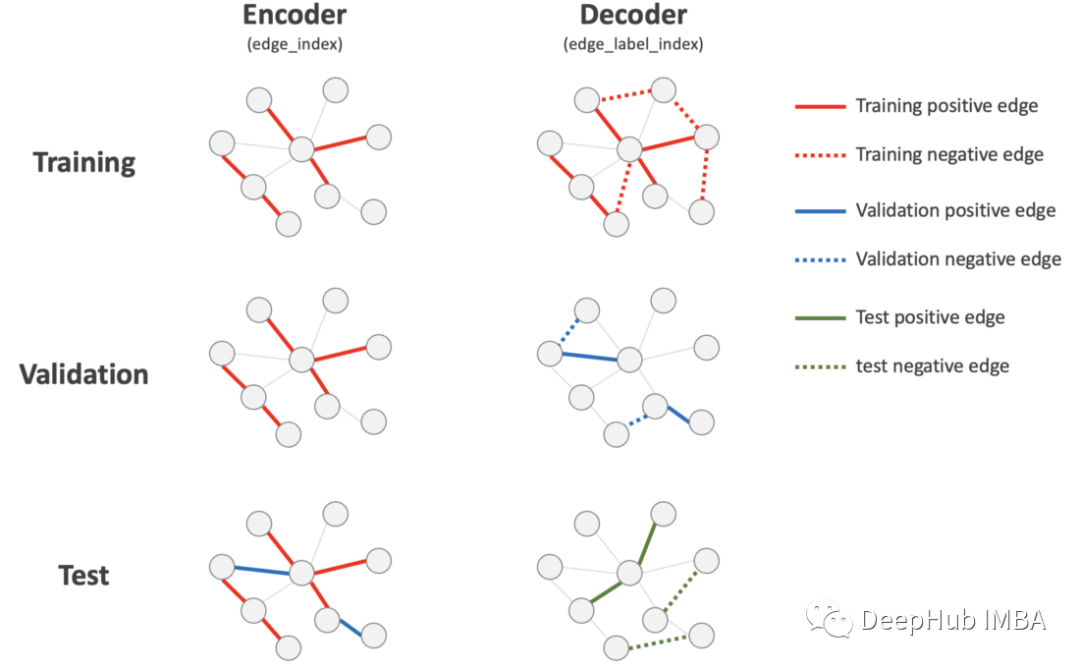
我们现在可以用下面的代码来训练和评估模型。

 model = Net(dataset.num_features, 128, 64).to(device)
 optimizer = torch.optim.Adam(params=model.parameters(), lr=0.01)
 criterion = torch.nn.BCEWithLogitsLoss()
 model = train_link_predictor(model, train_data, val_data, optimizer, criterion)
 
 test_auc = eval_link_predictor(model, test_data)
 print(f"Test: {test_auc:.3f}")

该模型的测试AUC为92.5%。

异常检测

再次使用Cora数据集进行异常检测任务，但它与前面的数据集略有不同:我们需要合成注入异常值。数据集有两种不同类型的异常值:

• 结构异常
• 密集连接的节点，而不是稀疏连接的规则节点
• 上下文的异常值
• 属性与相邻节点显著不同的节点

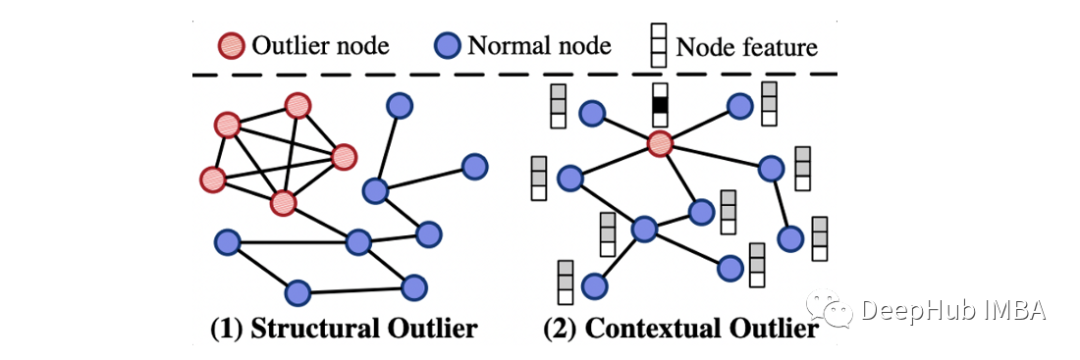
对于这个异常检测任务，需要使用的是PyGOD库，它是建立在PyG之上的一个图异常值检测库。可以通过PyGOD模块加载已经进行了异常值注入的Cora数据集。

 from pygod.utils import load_data
 
 graph = load_data('inj_cora')

下面的代码显示了异常值类型分布。

 Counter(graph.y.tolist())
 
 #Counter({0: 2570, 1: 68, 2: 68, 3: 2})

0:正常，1:仅上下文异常，2:结构异常，3:上下文和结构都异常

如果你对这些异常值是如何注入的感兴趣，可以查看关于异常值生成器模块的PyGOD文档，该文档解释了操作细节。这里我们需要注意的是标签y将只用于模型评估，而不是用于训练标签，因为我们正在训练一个无监督的模型。

为了检测这些异常点，我们训练了DOMINANT(Deep Anomaly Detection on Attributed Networks)模型。它是一个具有图卷积层的自编码器网络，其重构误差将是节点异常评分。该模型遵循以下步骤进行预测。

• 属性网络编码器使用三个图卷积层来处理输入图，从而创建节点嵌入。
• 结构重构解码器利用学习到的节点嵌入重构原始图边(即邻接矩阵)。它从每个可能的节点对计算节点嵌入的点积，在每个节点对上创建一个表示边缘存在的概率评分。
• 属性重构解码器使用获得的节点嵌入重构原始节点属性。它有一个图卷积层来预测属性值。
• 最后一步将上述两种解码器的重构误差在每个节点上进行加权平均合并，合并后的误差即为最终的误差/损失。这些最终的误差也是节点的异常评分。

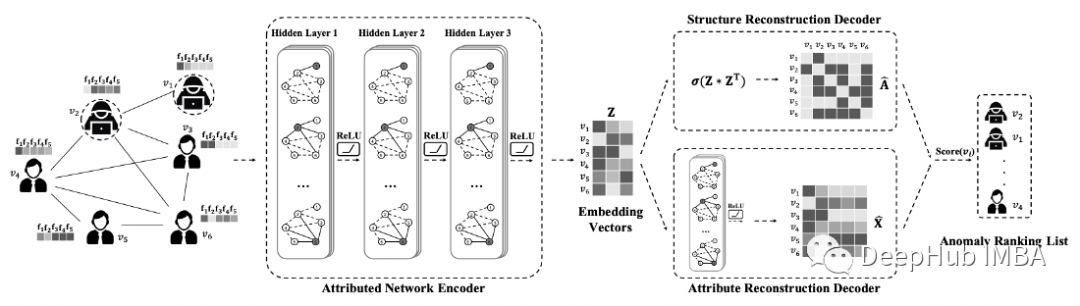
 from pygod.models import DOMINANT
 from sklearn.metrics import roc_auc_score, average_precision_score
 
 def train_anomaly_detector(model, graph):
     return model.fit(graph)
 
 def eval_anomaly_detector(model, graph):
 
     outlier_scores = model.decision_function(graph)
     auc = roc_auc_score(graph.y.numpy(), outlier_scores)
     ap = average_precision_score(graph.y.numpy(), outlier_scores)
     print(f'AUC Score: {auc:.3f}')
     print(f'AP Score: {ap:.3f}')
 
 
 graph.y = graph.y.bool()
 model = DOMINANT()
 model = train_anomaly_detector(model, graph)
 eval_anomaly_detector(model, graph)

模型的AUC为84.1%，平均精度为20.8%。这种差异很可能是由于目标不平衡造成的。由于这是一个无监督的模型，我们不可能期望得到一个非常精确的模型，但可以在原始论文中看到，它仍然优于任何其他流行的异常检测算法。

引用

本文的源代码可以在colab找到：

https://colab.research.google.com/drive/1Ksca_p4XrZjeN0A6jT5aYN6ARvwFVSbY?usp=sharing

引用如下：

• Benjamin Sanchez-Lengeling et al., A Gentle Introduction to Graph Neural Networks
• Ameya Daigavane et al., Understanding Convolutions on Graphs
• Francesco Casalegno, Graph Convolutional Networks — Deep Learning on Graphs
• Thomas N. Kipf, Max Welling, Semi-Supervised Classification with Graph Convolutional Networks (2017), ICLR 2017
• Thomas N. Kipf, Max Welling, Variational Graph Auto-Encoders (2016)
• Kaize Ding et al., Deep Anomaly Detection on Attributed Networks (2019)
• Kay Liu et al., Benchmarking Node Outlier Detection on Graphs (2022)

作者：Tomonori Masui