傅里叶变换+频域滤波
这个博客记得看看
cv2.imread()基本参数介绍
Mat cv::imread(const String & filename,int flags = IMREAD_COLOR)
retval = cv.imread(filename[, flags])# ilename:需要打开图片的路径,可以是绝对路径或者相对路径,路径中不能出现中文# flag:图像的通道和色彩信息(默认值为1)# flag = -1, 8位深度,原通道# flag = 0, 8位深度,1通道# flag = 1, 8位深度,3通道# flag = 2, 原深度, 1通道# flag = 3, 原深度, 3通道# flag = 4, 8位深度,3通道
参考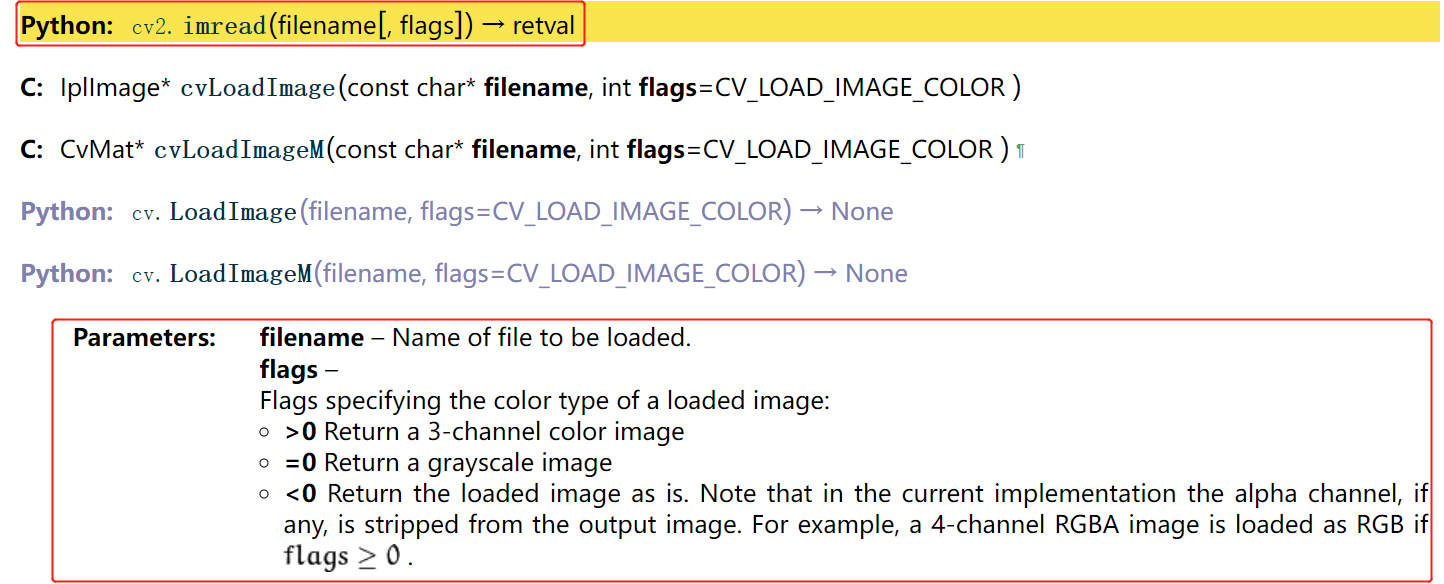
OpenCV官方文档
傅里叶变换
时域图像,频域图像
正常傅里叶变换后不做任何处理(不经过平移处理)的话应该是四角亮,中间暗
频域图像中亮的为低频信息,暗的为高频信息
自然图像一般都是低频信息多于高频信息
什么是频域
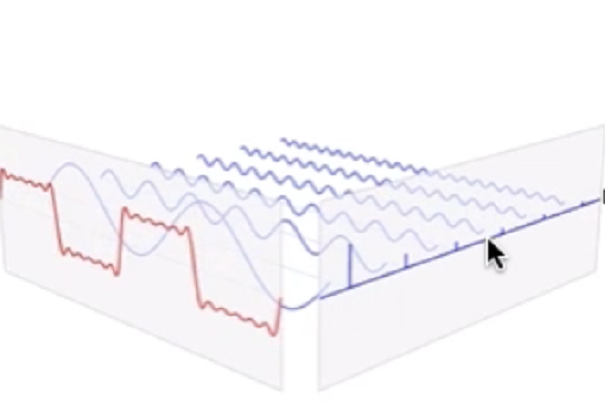
越往里面频率越来越高
振幅关于频域的函数
傅里叶变换的由来
傅里叶级数
对于任何以
2
π
2\pi
2π 为周期的函数,都可以由三角函数来拟合??
f
(
t
)
=
a
0
2
+
∑
n
=
1
+
∞
(
a
n
cos
n
t
+
b
n
sin
n
t
)
f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{+\infty}\left(a_{n} \cos n t+b_{n} \sin n t\right)
f(t)=2a0+n=1∑+∞(ancosnt+bnsinnt)
三角函数系正交性
∫
−
π
+
π
sin
k
x
cos
n
x
d
x
=
0
∫
−
π
+
π
sin
k
x
sin
n
x
d
x
=
{
0
,
k
≠
n
π
,
k
=
n
≠
0
∫
−
π
+
π
cos
k
x
cos
n
x
d
x
=
{
0
,
k
≠
n
π
,
k
=
n
≠
0
\begin{array}{l} \int_{-\pi}^{+\pi} \sin k x \cos n x d x=0 \\ \int_{-\pi}^{+\pi} \sin k x \sin n x d x=\left\{\begin{array}{l} 0, k \neq n \\ \pi, k=n \neq 0 \end{array}\right. \\ \int_{-\pi}^{+\pi} \cos k x \cos n x d x=\left\{\begin{array}{l} 0, k \neq n \\ \pi, k=n \neq 0 \end{array}\right. \end{array}
∫−π+πsinkxcosnxdx=0∫−π+πsinkxsinnxdx={0,k=nπ,k=n=0∫−π+πcoskxcosnxdx={0,k=nπ,k=n=0
正交性的证明:
1
)
:
∫
−
π
+
π
sin
k
x
cos
n
x
d
x
=
1
2
∫
−
π
+
π
[
sin
(
k
+
n
)
x
+
sin
(
k
−
n
)
x
]
d
x
(
积化和差
)
当
k
≠
n
时
,
上式
=
−
1
2
[
cos
(
k
+
n
)
x
k
+
n
+
cos
(
k
−
n
)
x
k
−
n
]
−
n
+
n
=
0
当
k
=
n
时
,
上式
=
∫
−
π
+
π
sin
k
x
cos
n
x
d
x
=
1
2
∫
−
π
+
π
sin
2
k
x
d
x
=
0
2
)
:
∫
−
π
+
π
sin
k
x
sin
n
x
d
x
=
1
2
∫
−
π
+
π
[
cos
(
k
−
n
)
x
−
cos
(
k
+
n
)
x
]
d
x
(
积化和差
)
当
k
≠
n
时,上式
=
1
2
[
sin
(
k
−
n
)
x
k
−
n
−
sin
(
k
+
n
)
x
k
+
n
]
−
π
+
π
=
0
当
k
=
n
≠
0
时
,
上式
=
1
2
∫
−
π
+
π
(
1
−
cos
2
k
x
)
d
x
=
π
1): \int_{-\pi}^{+\pi} \sin k x \cos n x d x=\frac{1}{2} \int_{-\pi}^{+\pi}[\sin (k+n) x+\sin (k-n) x] d x \quad (积化和差)\\ 当 k \neq n 时,上式 =-\frac{1}{2}\left[\frac{\cos (k+n) x}{k+n}+\frac{\cos (k-n) x}{k-n}\right]_{-n}^{+n}=0 \\ 当 k=n 时,上式 =\int_{-\pi}^{+\pi} \sin k x \cos n x d x=\frac{1}{2} \int_{-\pi}^{+\pi} \sin 2 k x d x=0 \\ \\ 2): \int_{-\pi}^{+\pi} \sin k x \sin n x d x=\frac{1}{2} \int_{-\pi}^{+\pi}[\cos (k-n) x-\cos (k+n) x] d x (积化和差)\\ 当 k \neq n 时,上式 =\frac{1}{2}\left[\frac{\sin (k-n) x}{k-n}-\frac{\sin (k+n) x}{k+n}\right]_{-\pi}^{+\pi}=0 \\ 当 k=n \neq 0 时,上式 =\frac{1}{2} \int_{-\pi}^{+\pi}(1-\cos 2 k x) d x=\pi
1):∫−π+πsinkxcosnxdx=21∫−π+π[sin(k+n)x+sin(k−n)x]dx(积化和差)当k=n时,上式=−21[k+ncos(k+n)x+k−ncos(k−n)x]−n+n=0当k=n时,上式=∫−π+πsinkxcosnxdx=21∫−π+πsin2kxdx=02):∫−π+πsinkxsinnxdx=21∫−π+π[cos(k−n)x−cos(k+n)x]dx(积化和差)当k=n时,上式=21[k−nsin(k−n)x−k+nsin(k+n)x]−π+π=0当k=n=0时,上式=21∫−π+π(1−cos2kx)dx=π
对傅里叶级数左右两边在
−
π
∼
π
-\pi \sim \pi
−π∼π上积分:
∫
−
π
+
π
f
(
t
)
d
t
=
a
0
2
∫
−
π
+
π
d
t
+
∑
n
=
1
+
∞
(
a
n
∫
−
π
+
π
cos
n
t
d
t
+
b
n
∫
−
π
+
π
sin
n
t
d
t
)
\int_{-\pi}^{+\pi} f(t) d t=\frac{a_{0}}{2} \int_{-\pi}^{+\pi} d t+\sum_{n=1}^{+\infty}\left(a_{n} \int_{-\pi}^{+\pi} \cos n t d t+b_{n} \int_{-\pi}^{+\pi} \sin n t d t\right)
∫−π+πf(t)dt=2a0∫−π+πdt+n=1∑+∞(an∫−π+πcosntdt+bn∫−π+πsinntdt)
由三角函数的正交性,可得后面的一串求和为0:
a
0
=
1
π
∫
−
π
π
f
(
t
)
d
t
a_{0}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(t)dt
a0=π1∫−ππf(t)dt
同理,在原式左右两端乘以
c
o
s
k
t
coskt
coskt再在
−
π
∼
+
π
-\pi \sim +\pi
−π∼+π上积分:
∫
−
π
+
π
f
(
t
)
cos
k
t
d
t
=
a
0
2
∫
−
π
+
π
cos
k
t
d
t
+
∑
n
=
1
+
∞
(
a
n
∫
−
π
+
π
cos
k
t
cos
n
t
d
t
+
b
n
∫
−
π
+
π
c
o
s
k
t
sin
n
t
d
t
)
\int_{-\pi}^{+\pi} f(t)\cos kt d t=\frac{a_{0}}{2} \int_{-\pi}^{+\pi}\cos kt d t+\sum_{n=1}^{+\infty}\left(a_{n} \int_{-\pi}^{+\pi}\cos kt \cos n t d t+b_{n} \int_{-\pi}^{+\pi} cos kt\sin n t \ d t\right)
∫−π+πf(t)cosktdt=2a0∫−π+πcosktdt+n=1∑+∞(an∫−π+πcosktcosntdt+bn∫−π+πcosktsinnt dt)
由三角函数系正交性得:
∫
−
π
+
π
f
(
t
)
cos
k
t
d
t
=
∑
n
=
1
+
∞
a
n
∫
−
π
+
π
cos
k
t
cos
n
t
d
t
=
a
k
π
\int_{-\pi}^{+\pi} f(t)\cos kt d t=\sum_{n=1}^{+\infty}a_{n} \int_{-\pi}^{+\pi}\cos kt \cos n t d t=a_{k}\pi
∫−π+πf(t)cosktdt=n=1∑+∞an∫−π+πcosktcosntdt=akπ
即:
a
k
=
1
π
∫
−
π
+
π
f
(
t
)
cos
k
t
d
t
a_{k}=\frac{1}{\pi}\int_{-\pi}^{+\pi}f(t)\cos kt dt
ak=π1∫−π+πf(t)cosktdt
同理:
b
k
=
1
π
∫
−
π
+
π
f
(
t
)
sin
k
t
d
t
b_{k}=\frac{1}{\pi}\int_{-\pi}^{+\pi}f(t)\sin kt dt
bk=π1∫−π+πf(t)sinktdt
已知傅里叶级数
f
(
t
)
=
a
0
2
+
∑
n
=
1
+
∞
(
a
n
cos
n
t
+
b
n
sin
n
t
)
f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{+\infty}\left(a_{n} \cos n t+b_{n} \sin n t\right)
f(t)=2a0+∑n=1+∞(ancosnt+bnsinnt)
T
=
2
π
\quad\quad T=2\pi
T=2π
为了使其更有一般性,而不是局限于
T
=
2
π
T=2\pi
T=2π
令:
φ
(
t
)
=
f
(
π
l
t
)
=
a
0
2
+
∑
n
=
1
+
∞
(
a
n
cos
n
π
l
t
+
b
n
sin
n
π
l
t
)
T
=
2
l
\varphi(t)=f\left(\frac{\pi}{l} t\right)=\frac{a_{0}}{2}+\sum_{n=1}^{+\infty}\left(a_{n} \cos \frac{n \pi}{l} t+b_{n} \sin \frac{n \pi}{l} t\right) \quad T=2 l
φ(t)=f(lπt)=2a0+∑n=1+∞(ancoslnπt+bnsinlnπt)T=2l
即它可以以任意实数
2
l
2l
2l 为周期
其中:
a
n
=
1
l
∫
−
l
+
l
f
(
t
)
cos
n
π
l
t
d
t
,
n
=
0
,
1
,
2
,
3...
a_{n}=\frac{1}{l}\int_{-l}^{+l}f(t)\cos \frac{n\pi}{l} tdt,\quad n=0,1,2,3...
an=l1∫−l+lf(t)coslnπtdt,n=0,1,2,3...
b
n
=
1
l
∫
−
l
+
l
f
(
t
)
sin
n
π
l
t
d
t
,
n
=
1
,
2
,
3...
b_{n}=\frac{1}{l}\int_{-l}^{+l}f(t)\sin \frac{n\pi}{l} tdt,\quad n=1,2,3...
bn=l1∫−l+lf(t)sinlnπtdt,n=1,2,3...
由欧拉公式
e
j
θ
=
cos
θ
+
j
sin
θ
e^{j\theta}=\cos \theta + j\sin \theta\quad\quad
ejθ=cosθ+jsinθ (
e
−
j
θ
=
cos
θ
−
j
sin
θ
e^{-j\theta}=\cos \theta - j\sin \theta
e−jθ=cosθ−jsinθ)得:
对
cos
θ
\cos \theta
cosθ
进行麦克劳林展开
对
sin
θ
\sin \theta
sinθ
进行麦克劳林展开
对
e
j
θ
e^{j\theta}
ejθ
进行麦克劳林展开
比较等式两端会发现左右相等,其中
j
j
j 为虚数单位,即
j
2
=
−
1
j^{2}=-1
j2=−1
cos
ω
t
=
1
2
e
j
ω
t
+
1
2
e
−
j
ω
t
sin
ω
t
=
j
(
1
2
e
−
j
ω
t
−
1
2
e
j
ω
t
)
\cos \omega t=\frac{1}{2}e^{j\omega t}+\frac{1}{2}e^{-j\omega t}\quad\quad\sin \omega t=j(\frac{1}{2}e^{-j\omega t}-\frac{1}{2}e^{j\omega t})
cosωt=21ejωt+21e−jωtsinωt=j(21e−jωt−21ejωt)
带入
φ
(
t
)
\varphi (t)
φ(t)得:
φ
(
t
)
=
a
0
2
+
∑
n
=
1
+
∞
[
a
n
2
(
e
j
n
π
l
t
+
e
−
j
n
π
l
t
)
−
j
b
n
2
(
e
j
n
π
l
t
−
e
−
j
n
π
l
t
)
]
=
a
0
2
+
∑
n
=
1
+
∞
[
a
n
−
j
b
n
2
.
e
j
n
π
l
t
+
a
n
+
j
b
n
2
.
e
−
j
n
π
l
t
]
\varphi(t)=\frac{a_{0}}{2}+\sum_{n=1}^{+\infty}\left[\frac{a_{n}}{2}\left(e^{j \frac{n \pi}{l} t}+e^{-j \frac{n \pi}{l} t}\right)-\frac{j b_{n}}{2}\left(e^{j \frac{n \pi}{l} t}-e^{-j \frac{n \pi}{l} t}\right)\right]\\ =\frac{a_{0}}{2}+\sum_{n=1}^{+\infty}\left[\frac{a_{n}-jb_{n}}{2}.e^{j \frac{n \pi}{l} t}+\frac{a_{n}+jb_{n}}{2}.e^{-j \frac{n \pi}{l} t}\right]
φ(t)=2a0+n=1∑+∞[2an(ejlnπt+e−jlnπt)−2jbn(ejlnπt−e−jlnπt)]=2a0+n=1∑+∞[2an−jbn.ejlnπt+2an+jbn.e−jlnπt]
令
c
0
=
a
0
2
,
c
n
=
a
n
−
j
b
n
2
,
c
−
n
=
a
n
+
j
b
n
2
c_{0}=\frac{a_{0}}{2}, c_{n}=\frac{a_{n}-jb_{n}}{2}, c_{-n}=\frac{a_{n}+jb_{n}}{2}
c0=2a0,cn=2an−jbn,c−n=2an+jbn
则
φ
(
t
)
=
c
0
+
∑
n
=
1
+
∞
[
c
n
.
e
j
n
π
l
t
+
c
−
n
.
e
−
j
n
π
l
t
]
\varphi(t)=c_{0} + \sum_{n=1}^{+\infty}\left[c_{n}.e^{j\frac{n\pi}{l}t}+c_{-n}.e^{-j\frac{n\pi}{l}t}\right]
φ(t)=c0+n=1∑+∞[cn.ejlnπt+c−n.e−jlnπt]
由于:
c
0
=
c
0
.
e
j
0
π
l
t
c_{0}=c_{0}.e^{j\frac{0\pi}{l}t}
c0=c0.ejl0πt
于是:
φ
(
t
)
=
∑
n
=
−
∞
+
∞
c
n
.
e
j
n
π
t
l
\varphi(t)=\sum_{n=-\infty}^{+\infty}c_{n}.e^{j\frac{n\pi t}{l}}
φ(t)=n=−∞∑+∞cn.ejlnπt
其中
c
0
=
a
0
2
,
c
n
=
a
n
−
j
b
n
2
,
c
−
n
=
a
n
+
j
b
n
2
c_{0}=\frac{a_{0}}{2}, c_{n}=\frac{a_{n}-jb_{n}}{2}, c_{-n}=\frac{a_{n}+jb_{n}}{2}
c0=2a0,cn=2an−jbn,c−n=2an+jbn
又因为:
a
n
=
1
l
∫
−
l
+
l
f
(
t
)
cos
n
π
l
t
d
t
,
n
=
0
,
1
,
2
,
3...
a_{n}=\frac{1}{l}\int_{-l}^{+l}f(t)\cos \frac{n\pi}{l} tdt,\quad n=0,1,2,3...
an=l1∫−l+lf(t)coslnπtdt,n=0,1,2,3...
b
n
=
1
l
∫
−
l
+
l
f
(
t
)
sin
n
π
l
t
d
t
,
n
=
1
,
2
,
3...
b_{n}=\frac{1}{l}\int_{-l}^{+l}f(t)\sin \frac{n\pi}{l} tdt,\quad n=1,2,3...
bn=l1∫−l+lf(t)sinlnπtdt,n=1,2,3...
{
c
0
=
a
0
2
=
1
2
l
∫
−
l
l
f
(
t
)
d
t
=
1
2
l
∫
−
l
l
f
(
t
)
e
−
j
0
π
t
l
d
t
c
n
=
a
n
−
j
b
n
2
=
1
2
[
1
l
∫
−
l
l
f
(
t
)
cos
n
π
l
t
d
t
−
j
1
l
∫
−
l
l
f
(
t
)
sin
n
π
l
t
d
t
]
=
1
2
l
∫
−
l
l
f
(
t
)
e
−
j
n
π
t
l
d
t
c
−
n
=
a
n
+
j
b
n
2
=
1
2
[
1
l
∫
−
l
l
f
(
t
)
cos
n
π
l
t
d
t
+
j
1
l
∫
−
l
l
f
(
t
)
sin
n
π
l
t
d
t
]
=
1
2
l
∫
−
l
l
f
(
t
)
e
n
π
π
t
l
d
t
\left\{\begin{array}{l} c_{0}=\frac{a_{0}}{2}=\frac{1}{2 l} \int_{-l}^{l} f(t) d t=\frac{1}{2 l} \int_{-l}^{l} f(t) e^{-j \frac{0 \pi t}{l}} d t \\ c_{n}=\frac{a_{n}-j b_{n}}{2}=\frac{1}{2}\left[\frac{1}{l} \int_{-l}^{l} f(t) \cos \frac{n \pi}{l} t d t-j \frac{1}{l} \int_{-l}^{l} f(t) \sin \frac{n \pi}{l} t d t\right]=\frac{1}{2 l} \int_{-l}^{l} f(t) e^{-j \frac{n \pi t}{l}} d t \\ c_{-n}=\frac{a_{n}+j b_{n}}{2}=\frac{1}{2}\left[\frac{1}{l} \int_{-l}^{l} f(t) \cos \frac{n \pi}{l} t d t+j \frac{1}{l} \int_{-l}^{l} f(t) \sin \frac{n \pi}{l} t d t\right]=\frac{1}{2 l} \int_{-l}^{l} f(t) e^{\frac{n \pi \pi t}{l}} d t \end{array}\right.
⎩⎨⎧c0=2a0=2l1∫−llf(t)dt=2l1∫−llf(t)e−jl0πtdtcn=2an−jbn=21[l1∫−llf(t)coslnπtdt−jl1∫−llf(t)sinlnπtdt]=2l1∫−llf(t)e−jlnπtdtc−n=2an+jbn=21[l1∫−llf(t)coslnπtdt+jl1∫−llf(t)sinlnπtdt]=2l1∫−llf(t)elnππtdt
综上,
c
n
=
1
2
l
∫
−
l
+
l
f
(
t
)
e
−
j
n
π
t
l
d
t
,
n
=
0
,
±
1
,
±
2
,
…
c_{n}=\frac{1}{2l}\int_{-l}^{+l}f(t)e^{-j\frac{n\pi t}{l}}dt,\quad\quad n=0, \pm 1, \pm 2, \ldots
cn=2l1∫−l+lf(t)e−jlnπtdt,n=0,±1,±2,…
由上
φ
(
t
)
=
∑
n
=
−
∞
+
∞
c
n
.
e
j
n
π
t
l
\varphi(t)=\sum_{n=-\infty}^{+\infty}c_{n}.e^{j\frac{n\pi t}{l}}
φ(t)=∑n=−∞+∞cn.ejlnπt,
c
n
=
1
2
l
∫
−
l
+
l
f
(
ω
)
e
−
j
n
π
ω
l
d
ω
,
n
=
0
,
±
1
,
±
2
,
…
c_{n}=\frac{1}{2l}\int_{-l}^{+l}f(\omega)e^{-j\frac{n\pi \omega}{l}}d\omega,\quad\quad n=0, \pm 1, \pm 2, \ldots
cn=2l1∫−l+lf(ω)e−jlnπωdω,n=0,±1,±2,…
将
c
n
c_{n}
cn带入
φ
(
t
)
\varphi(t)
φ(t)得:
φ
(
t
)
=
∑
n
=
−
∞
+
∞
1
2
l
∫
−
l
l
f
(
ω
)
e
−
j
n
π
ω
l
d
ω
⋅
e
j
n
π
t
l
=
∑
n
=
−
∞
+
∞
1
2
l
∫
−
l
l
f
(
ω
)
e
n
π
(
t
−
ω
)
l
d
ω
\varphi(t)=\sum_{n=-\infty}^{+\infty} \frac{1}{2 l} \int_{-l}^{l} f(\omega) e^{-j \frac{n \pi \omega}{l}} d \omega \cdot e^{j \frac{n \pi t}{l}}=\sum_{n=-\infty}^{+\infty} \frac{1}{2 l} \int_{-l}^{l} f(\omega) e^{\frac{n \pi(t-\omega)}{l}} d \omega
φ(t)=n=−∞∑+∞2l1∫−llf(ω)e−jlnπωdω⋅ejlnπt=n=−∞∑+∞2l1∫−llf(ω)elnπ(t−ω)dω
对于非周期函数,使其更具有一般性,可看做周期无穷大:
f
(
t
)
=
lim
l
→
+
∞
φ
(
t
)
=
lim
l
→
+
∞
∑
n
=
−
∞
+
∞
1
2
l
∫
−
l
l
f
(
z
)
e
j
n
π
(
t
−
z
)
l
d
z
=
lim
l
→
+
∞
∑
n
=
−
∞
+
∞
1
2
π
∫
−
l
l
f
(
z
)
e
j
n
π
(
t
−
z
)
l
d
z
⋅
π
l
\begin{array}{l} f(t)=\lim _{l \rightarrow+\infty} \varphi(t)=\lim _{l \rightarrow+\infty} \sum_{n=-\infty}^{+\infty} \frac{1}{2 l} \int_{-l}^{l} f(z) e^{j \frac{n \pi(t-z)}{l}} d z\\ \\ =\lim _{l \rightarrow+\infty} \sum_{n=-\infty}^{+\infty} \frac{1}{2 \pi} \int_{-l}^{l} f(z) e^{j \frac{n \pi(t-z)}{l}} d z \cdot \frac{\pi}{l} \end{array}
f(t)=liml→+∞φ(t)=liml→+∞∑n=−∞+∞2l1∫−llf(z)ejlnπ(t−z)dz=liml→+∞∑n=−∞+∞2π1∫−llf(z)ejlnπ(t−z)dz⋅lπ
令:
ω
n
=
n
π
l
,
Δ
ω
=
π
l
\omega_{n}=\frac{n \pi}{l}, \Delta \omega=\frac{\pi}{l}
ωn=lnπ,Δω=lπ
f
(
t
)
=
lim
l
→
+
∞
∑
n
=
−
∞
+
∞
1
2
π
∫
−
l
l
f
(
z
)
e
j
ω
n
(
t
−
z
)
d
z
⋅
Δ
ω
=
1
2
π
∫
−
∞
+
∞
[
∫
−
∞
+
∞
f
(
z
)
e
j
ω
(
t
−
z
)
d
z
]
d
ω
\begin{array}{l} f(t)=\lim _{l \rightarrow+\infty} \sum_{n=-\infty}^{+\infty} \frac{1}{2 \pi} \int_{-l}^{l} f(z) e^{j \omega_{n}(t-z)} d z \cdot \Delta \omega=\frac{1}{2 \pi} \int_{-\infty}^{+\infty}\left[\int_{-\infty}^{+\infty} f(z) e^{j \omega(t-z)} d z\right] d \omega \end{array}
f(t)=liml→+∞∑n=−∞+∞2π1∫−llf(z)ejωn(t−z)dz⋅Δω=2π1∫−∞+∞[∫−∞+∞f(z)ejω(t−z)dz]dω
上面得到了一个二重的反常积分
f
(
t
)
=
1
2
π
∫
−
∞
+
∞
[
∫
−
∞
+
∞
f
(
z
)
e
j
ω
(
t
−
z
)
d
z
]
d
ω
=
1
2
π
∫
−
∞
+
∞
[
∫
−
∞
+
∞
f
(
z
)
e
−
j
ω
z
d
z
]
e
j
ω
t
d
ω
\begin{array}{l} f(t)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty}\left[\int_{-\infty}^{+\infty} f(z) e^{j \omega(t-z)} d z\right] d \omega\\=\frac{1}{2 \pi} \int_{-\infty}^{+\infty}\left[\int_{-\infty}^{+\infty} f(z) e^{-j \omega z} d z\right]e^{j\omega t} d \omega \end{array}
f(t)=2π1∫−∞+∞[∫−∞+∞f(z)ejω(t−z)dz]dω=2π1∫−∞+∞[∫−∞+∞f(z)e−jωzdz]ejωtdω
令:
F
(
ω
)
=
∫
−
∞
+
∞
f
(
t
)
e
−
j
ω
t
d
t
F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt\quad\quad\quad
F(ω)=∫−∞+∞f(t)e−jωtdt频域
则:
f
(
t
)
=
1
2
π
∫
−
∞
+
∞
F
(
ω
)
e
j
ω
t
d
ω
f(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{j\omega t}d\omega\quad\quad
f(t)=2π1∫−∞+∞F(ω)ejωtdω时域
这就是傅里叶变换对
傅里叶变换算法 DFT, FFT
DFT:Discrete Fourier Transform
FFT:Fast Fourier Transform
计算机智能处理离散数据,故对连续的傅里叶变换对:
F
(
ω
)
=
∫
−
∞
+
∞
f
(
t
)
e
−
j
ω
t
d
t
,
F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt,\quad\quad\quad
F(ω)=∫−∞+∞f(t)e−jωtdt,
f
(
t
)
=
1
2
π
∫
−
∞
+
∞
F
(
ω
)
e
j
ω
t
d
ω
f(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{j\omega t}d\omega\quad\quad
f(t)=2π1∫−∞+∞F(ω)ejωtdω
做
N
N
N点等距采样得离散变换对:
F
(
u
)
=
∑
x
=
0
N
−
1
f
(
x
)
e
−
j
2
π
N
x
u
f
(
x
)
=
1
N
∑
u
=
0
N
−
1
F
(
u
)
e
j
2
π
N
x
u
F(u)=\sum_{x=0}^{N-1} f(x) e^{-j \frac{2 \pi}{N} x u} \quad f(x)=\frac{1}{N} \sum_{u=0}^{N-1} F(u) e^{j \frac{2 \pi}{N} x u}
F(u)=x=0∑N−1f(x)e−jN2πxuf(x)=N1u=0∑N−1F(u)ejN2πxu
ω
=
2
π
u
N
\omega=\frac{2\pi u}{N}
ω=N2πu,
u
u
u是频率,
T
=
2
π
u
,
ω
=
T
N
T=2\pi u, \omega=\frac{T}{N}
T=2πu,ω=NT
以上为一元函数的情况
扩展到二元函数:
F
(
u
,
v
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
(
u
x
M
+
v
y
N
)
,
f
(
x
,
y
)
=
1
M
N
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
F
(
u
,
v
)
e
j
2
π
(
u
x
M
+
v
y
N
)
F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})},\quad f(x,y)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})}
F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy),f(x,y)=MN1u=0∑M−1v=0∑N−1F(u,v)ej2π(Mux+Nvy)
以上即为DFT公式
由DFT正向变换公式:
F
(
u
,
v
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
(
u
x
M
+
v
y
N
)
=
∑
x
=
0
M
−
1
e
−
j
2
π
u
x
M
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
v
y
N
=
∑
x
=
0
M
−
1
[
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
v
y
N
]
e
−
j
2
π
u
x
M
\begin{array}{l} F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j 2 \pi\left(\frac{u x}{M}+\frac{v y}{N}\right)}\\ =\sum_{x=0}^{M-1} e^{-j 2 \pi \frac{u x}{M}} \sum_{y=0}^{N-1} f(x, y) e^{-j 2 \pi \frac{v y}{N}}\\ =\sum_{x=0}^{M-1}\left[\sum_{y=0}^{N-1} f(x, y) e^{-j 2 \pi \frac{v y}{N}}\right] e^{-j 2 \pi \frac{u x}{M}} \end{array}
F(u,v)=∑x=0M−1∑y=0N−1f(x,y)e−j2π(Mux+Nvy)=∑x=0M−1e−j2πMux∑y=0N−1f(x,y)e−j2πNvy=∑x=0M−1[∑y=0N−1f(x,y)e−j2πNvy]e−j2πMux
由此可见,二元DFT可分为两个一元DFT的叠加。若用两个一元DFT代替二元DFT,算法复杂度由
O
(
M
2
N
2
)
O(M^{2}N^{2})
O(M2N2)降为
O
(
M
2
N
+
M
N
2
)
O(M^{2}N + MN^{2})
O(M2N+MN2)
有点像那个高斯核的卷积,一个卷积核可以拆分为两个卷积核的意思
可以先对图像进行一个方向上的离散傅里叶变换,再对所得到的图像进行另一个方向上的离散傅里叶变换, 就可以得到直接做二维的离散傅里叶变换相同的效果,这样可以降低复杂度,4次的变为3次
类似地,对反向变换公式同样适用。
通常,我们使用
F
(
u
−
M
2
,
v
−
N
2
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
(
−
1
)
x
+
y
f
(
x
,
y
)
e
−
j
2
π
(
u
x
M
+
v
y
N
)
F(u-\frac{M}{2},v-\frac{N}{2})=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}(-1)^{x+y} f(x, y) e^{-j 2 \pi\left(\frac{u x}{M}+\frac{v y}{N}\right)}
F(u−2M,v−2N)=x=0∑M−1y=0∑N−1(−1)x+yf(x,y)e−j2π(Mux+Nvy)
代替原式(将低频成分移动到图像中央,好看)
相当于在每个位置乘上
( − 1 ) x + y (-1)^{x+y} (−1)x+y就可以把低频成分移动到图像中央
这是因为
F
(
u
−
M
2
,
v
−
N
2
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
[
(
u
−
M
2
)
x
M
+
(
v
−
N
2
)
y
N
]
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
(
u
x
M
+
v
y
N
)
.
e
j
π
(
x
+
y
)
F(u-\frac{M}{2},v-\frac{N}{2})=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}f(x,y)e^{-j2\pi \left[\frac{(u-\frac{M}{2})x}{M}+\frac{(v-\frac{N}{2})y}{N}\right]}\\ =\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (\frac{ux}{M}+\frac{vy}{N})}.e^{j\pi(x+y)}
F(u−2M,v−2N)=x=0∑M−1y=0∑N−1f(x,y)e−j2π[M(u−2M)x+N(v−2N)y]=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy).ejπ(x+y)
e
j
π
=
cos
π
+
j
sin
π
,
sin
π
=
0
,
cos
π
=
−
1
e^{j\pi} = \cos \pi +j\sin \pi, \sin \pi=0,\cos \pi=-1
ejπ=cosπ+jsinπ,sinπ=0,cosπ=−1
由欧拉公式有
e
j
π
=
−
1
e^{j\pi} = -1
ejπ=−1,于是
F
(
u
−
M
2
,
v
−
N
2
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
(
−
1
)
x
+
y
f
(
x
,
y
)
e
−
j
2
π
(
u
x
M
+
v
y
N
)
F(u-\frac{M}{2},v-\frac{N}{2}) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1}(-1)^{x+y}f(x,y)e^{-j2\pi(\frac{ux}{M} + \frac{vy}{N})}
F(u−2M,v−2N)=x=0∑M−1y=0∑N−1(−1)x+yf(x,y)e−j2π(Mux+Nvy)
还可以继续优化为FFT
下面为 基2时间抽取的FFT算法:首先,将二维DFT等效为两个一维DFT的叠加。此时时间复杂度为O ( M 2 N + M N 2 ) O(M^{2}N + MN^{2}) O(M2N+MN2)
对于每个一维DFT还可以进行如下优化:
根据一维的DFT公式:
F ( u ) = ∑ x = 0 N − 1 f ( x ) e − j 2 π N x u F(u)=\sum_{x=0}^{N-1} f(x) e^{-j \frac{2 \pi}{N} x u} F(u)=∑x=0N−1f(x)e−jN2πxu把 F ( u ) F(u) F(u)分成奇数和偶数两项
F
(
u
)
=
∑
x
=
0
N
−
1
f
(
x
)
e
−
j
2
π
N
x
u
=
∑
x
=
0
N
2
−
1
f
(
2
x
)
e
−
j
2
π
N
2
x
u
+
∑
x
=
0
N
2
−
1
f
(
2
x
+
1
)
e
−
j
2
π
N
(
2
x
+
1
)
u
=
∑
x
=
0
N
2
−
1
f
(
2
x
)
e
−
j
2
π
N
2
x
u
+
e
−
j
2
π
N
u
⋅
∑
x
=
0
N
2
−
1
f
(
2
x
+
1
)
e
−
j
2
π
N
2
x
u
\begin{aligned} F(u) &=\sum_{x=0}^{N-1} f(x) e^{-j \frac{2 \pi}{N} x u} \\ &=\sum_{x=0}^{\frac{N}{2}-1} f(2 x) e^{-j \frac{2 \pi}{N} 2 x u}+\sum_{x=0}^{\frac{N}{2}-1} f(2 x+1) e^{-j \frac{2 \pi}{N}(2 x+1) u} \\ &=\sum_{x=0}^{\frac{N}{2}-1} f(2 x) e^{-j \frac{2 \pi}{N} 2 x u}+e^{-j \frac{2 \pi}{N} u} \cdot \sum_{x=0}^{\frac{N}{2}-1} f(2 x+1) e^{-j \frac{2 \pi}{N} 2 x u} \end{aligned}
F(u)=x=0∑N−1f(x)e−jN2πxu=x=0∑2N−1f(2x)e−jN2π2xu+x=0∑2N−1f(2x+1)e−jN2π(2x+1)u=x=0∑2N−1f(2x)e−jN2π2xu+e−jN2πu⋅x=0∑2N−1f(2x+1)e−jN2π2xu
其中我们称
e − j 2 π N 2 x u e^{-j\frac{2\pi}{N}2xu} e−jN2π2xu为**旋转因子**
可证
e
−
j
2
π
N
(
u
+
N
2
)
=
−
e
−
j
2
π
N
u
e^{-j\frac{2\pi}{N}(u+\frac{N}{2})} = -e^{-j\frac{2\pi}{N}u}
e−jN2π(u+2N)=−e−jN2πu,于是
F
(
u
)
=
{
∑
x
=
0
N
2
−
1
f
(
2
x
)
e
−
j
2
π
N
2
x
u
+
e
−
j
2
π
N
u
⋅
∑
x
=
0
N
2
−
1
f
(
2
x
+
1
)
e
−
j
2
π
N
2
x
u
,
u
<
N
2
∑
x
=
0
N
2
−
1
f
(
2
x
)
e
−
j
2
π
N
2
x
u
−
e
−
j
2
π
N
(
u
−
N
2
)
⋅
∑
x
=
0
N
2
−
1
f
(
2
x
+
1
)
e
−
j
2
π
N
2
x
u
,
u
>
N
2
F(u)=\left\{\begin{array}{l} \sum_{x=0}^{\frac{N}{2}-1} f(2 x) e^{-j \frac{2 \pi}{N} 2 x u}+e^{-j \frac{2 \pi}{N} u} \cdot \sum_{x=0}^{\frac{N}{2}-1} f(2 x+1) e^{-j \frac{2 \pi}{N} 2 x u}, u<\frac{N}{2} \\ \sum_{x=0}^{\frac{N}{2}-1} f(2 x) e^{-j \frac{2 \pi}{N} 2 x u}-e^{-j \frac{2 \pi}{N}\left(u-\frac{N}{2}\right)} \cdot \sum_{x=0}^{\frac{N}{2}-1} f(2 x+1) e^{-j \frac{2 \pi}{N} 2 x u}, u>\frac{N}{2} \end{array}\right.
F(u)={∑x=02N−1f(2x)e−jN2π2xu+e−jN2πu⋅∑x=02N−1f(2x+1)e−jN2π2xu,u<2N∑x=02N−1f(2x)e−jN2π2xu−e−jN2π(u−2N)⋅∑x=02N−1f(2x+1)e−jN2π2xu,u>2N
上面两个和式是与原问题相同的子问题,但规模减半,并且
u
>
N
2
u>\frac{N}{2}
u>2N时,可用之前计算过的值,无需重复计算。使用递归实现,时间复杂度降为
O
(
N
(
log
2
N
)
+
M
(
log
2
M
)
)
O\left(N\left(\log _{2} N\right)+M\left(\log _{2} M\right)\right)
O(N(log2N)+M(log2M))
灰度图
灰度图就是单通道图像,而单通道图是指维度数为2,即有h,w的图像。
而灰度就是没有色彩,RGB色彩分量全部相等(可将这点与下文的RGB图进行对比)。那么灰度图的每个像素点就只有一个值表示颜色,像素值的范围就是[0~255]。如使用RGB表示灰度为100的图像,三通道灰度图即RGB(100,100,100),而单通道灰度图只有其中一个有值。
简而言之,灰度图就是黑白图。
图像通道在RGB色彩模式下就是指在下就是指那单独的红色R、绿色G、蓝色B部分。
与灰度图不同之处在于,该图的每个像素点都有3个值表示颜色,也叫3通道。如RGB(10,47,200).
每个点若位深度为8,即8bit,那么就是灰度图。
若位深度为24,即RGB图
参考
版权归原作者 乖乖怪123 所有, 如有侵权,请联系我们删除。