Softmax是一种数学函数,通常用于将一组任意实数转换为表示概率分布的实数。其本质上是一种归一化函数,可以将一组任意的实数值转化为在[0, 1]之间的概率值,因为softmax将它们转换为0到1之间的值,所以它们可以被解释为概率。如果其中一个输入很小或为负,softmax将其变为小概率,如果输入很大,则将其变为大概率,但它将始终保持在0到1之间。
Softmax是逻辑回归的一种推广,可以用于多分类任务,其公式与逻辑回归的sigmoid函数非常相似。只有当分类是互斥的,才可以在分类器中使用softmax函数,也就是说只能是多元分类(即数据只有一个标签),而不能是多标签分类(即一条数据可能有多个标签)。
许多多层神经网络输出层的最后一层是一个全连接层,输出是一个实数向量,这个向量通常代表了每个类别的得分或置信度。为了将这些得分转换为概率分布,通常会使用softmax函数。因为它将分数转换为规范化的概率分布,可以显示给用户或用作其他系统的输入。所以通常附加一个softmax函数在神经网络的最后一层之后。
Softmax函数的公式
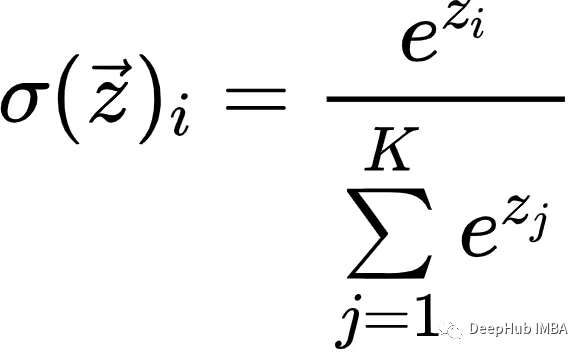
softmax函数的输入是一个包含K个元素的向量,其中不带箭头的z表示向量的一个元素:
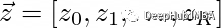
下面是一个例子:
其中分子的函数可视化如下:
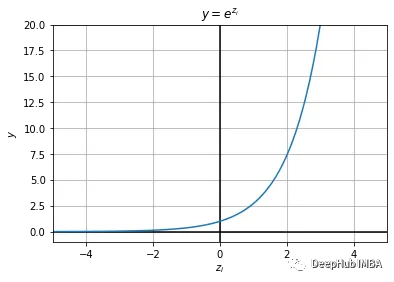
Softmax的分子将指数函数应用于向量的每个元素,对于最高的输入值返回最高的输出值。因为它的范围是(0,∞),所以任何负数也变成正数。这可以从上面的图和下面的的区间中看出。
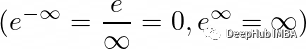
Softmax分母中的求和是通过确保函数的和为1来标准化每个元素,创建一个概率分布。所有的指数元素加在一起,所以当每个指数元素除以这个和时,它将是它的一个百分比。[5,7,10]的指数元素之和如下:

下面这个例子将使用一个3元素向量[5,7,10]来演示softmax。
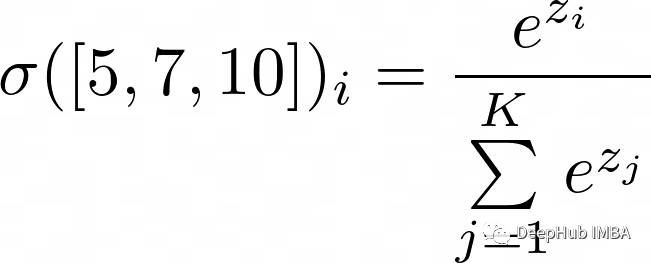
i表示向量的每个元素单独传入,这样会创建一个包含K个元素的向量作为输出。由于K = 3,函数将被计算三次:
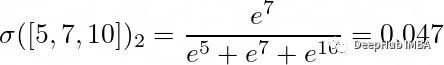
输出为[0.006,0.047,0.946],总和约为1。
我们可以使用框架中已经实现的softmax函数可以用来自动计算,例如PyTorch中:
import torch
# set the vector to a tensor
z = torch.Tensor([5, 7, 10])
# apply softmax
softmax = torch.exp(z) / torch.sum(torch.exp(z))
#tensor([0.0064, 0.0471, 0.9465])
对于矩阵来说,也是一样的,我们下面先手动计算矩阵的softmax

softmax = torch.exp(x) / torch.sum(torch.exp(x), axis=1, keepdims=True)
得到了结果:
tensor([[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652]])
每个向量加起来大约是1。但是这里有一个问题:输入向量不同但是结果是相同的。为什么会这样?
因为只要指数值之间的距离相同,结果就是是相同的,看看下面的计算:

为了验证我们的计算,可以使用框架内置的函数,比如torch的nn.Softmax
import torch.nn as nn
x = torch.Tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# sum each row
softmax_layer = nn.Softmax(dim=1)
output = softmax_layer(x)
结果是一样的
tensor([[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652]])
说明我们的实现是没有问题的,但是还要说明一点,尽量使用框架提供的计算,因为这样会经过优化,速度会比我们手动实现快很多。
作者:Hunter Phillips