本文为人工智能与机器学习课程大作业第二部分(二、函数逼近)
本文仅作学习参考使用!
** 其他章节跳转:**
一、知识工程基础
二、函数逼近
三、模糊逻辑
四、函数优化
目 录
** 二、函数逼近**
Q:用BP网络和RBF网络研究如下非线性函数的逼近问题:
要求:
1****、先获取两组数据,一组作为训练集,另一组作为测试集,用训练集训练网络,用测试集检验训练结果;
2****、改变隐层神经元数目、训练算法、学习率及最大迭代次数等参数,分析它们对逼近精度的影响;
3****、两种网络的逼近结果对比分析。
2.1 BP网络
2.1.1 BP神经网络原理
BP神经网络也被称为误差反向传播神经网络,它是由非线性变换单元组成的前馈网络,一般的多层前馈网络也指BP神经网络[1]。
BP学习算法是训练人工神经网络的基本方法,它也是一个非常重要且经典的学习算法,其实质是求解误差函数的最小值问题,利用它可以实现多层前馈神经网络权值的调节。这种学习算法的提出对人工神经网络发展起到了很大的推动作用。
神经网络的信息处理功能是由网络单元(神经元)的输入输出特性(激活特性),网络的拓扑结构(神经元的连接方式)、连接权的大小(突触联系强度)和神经元的阈值(视为特殊的连接权)所决定的。神经元是神经网络最基本的组成部分,其结构模型如图2-1所示。
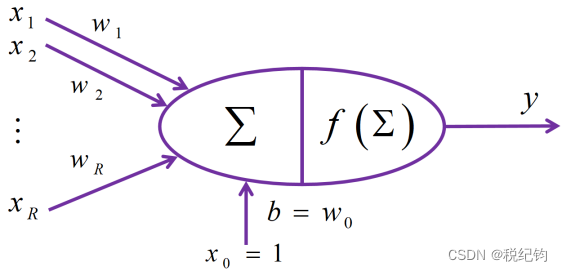
图2-1 神经元结构模型
其中xi(i=1,2,...,R)为神经元输入,wi(i=1,2,...,R)代表神经元之间的连接权值,b=w0为阈值(偏置值),若将xo=1也视为神经元输入,则w0可视为特殊的连接权,f为传输函数(激活函数),y为神经元输出,有:
令X=(x1 x2 ... xR),W=(w1 w2 ... wR)T,XW+b=n则有:
传递函数f可为线性或非线性函数,常用的传递函数有hardlim(硬极限传递函数)、purelin(线性传递函数)和logsig(对数型传递函数)。
通常所说的BP模型是神经网络模型中使用最广泛的一类。从结构上讲,BP网络是一种分层型的典型多层网络,具有输入层、隐含层和输出层,层与层之间多采用全连接的方式。同一层单元之间不存在相互连接。图2-2给出了一个典型的3层BP神经网络结构。与多层感知机相比,二者是类似的,但差异也是显著的。BP网络和感知机的主要区别在于每一层的权值都可以通过学习来调整。由于logsig函数是可微的,所以BP网络采用该函数作为传输函数。
BP网络可被看成是一个从输入到输出的高度非线性映射,即F:Rm->Rn,Y=f(n)。对于样本集合输入:输入xi(Rm)和输出yi(Rn),可以被认为存在某一映射g,使g(xi)=yi,i=1,2,...,p。现要求有一个映射f,使得在某种意义下(通常是最小二乘意义下),f是g的最佳逼近。Hechat-Nielsen证明了如下的Kolmogorov定理:给定任一连续函数f:U->R,这里U是闭单位区间[0,1],f可以精确地用一个3层前馈网络实现,此网络的第一层有m个处理单元,中间层有个2m+1处理单元,第三层有n个处理单元。

图2-2 3层BP神经网络结构图
2.1.2 基于BP神经网络的非线性函数逼近
需要逼近的函数为:
需要注意的是,更新迭代次数在这里的非线性函数逼近问题中,并没有太多的实际作用,由于函数较简单,因此更多的会考虑MSE、SSE或者RMSE等评价指标,而不会太多关注复杂度的问题。因此我将BP中epochs设置为无穷大,用1000000表示。
原始非线性函数如图2-3所示。按照8:2的比例将[-10,10]的区间分为训练集和测试集,即训练集为[-10,6),测试集为[6,10]。需要指出的是,因为要修改如隐含层层数、神经元个数、学习率、训练算法、激活函数等网络模型参数,因此为了防止过拟合是需要用到验证集的,这也是在神经网络中必须使用的手段,因此在修改网络参数部分,我再将训练集中的一部分划分为验证集,最终得到训练集:验证集:测试集=6:2:2。
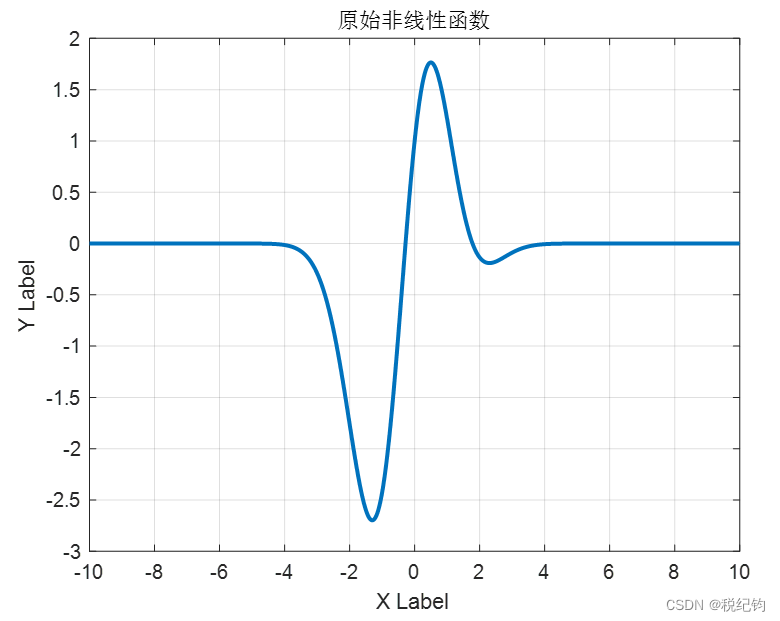
图2-3 原始非线性函数
在newff中的训练函数及其特点和使用场景有如表2-1所示。
表2-1 训练函数及其特点和使用场景
函数名称
特点及使用场景
traingd
基本梯度下降法,收敛速度比较慢
traingdm
带有动量项的梯度下降法, 通常要比traingd 速度快
traingdx
带有动量项的自适应学习算法, 速度要比traingdm 快
trainer
弹性BP 算法, 具有收敛速度快和占用内存小的优点
traincgf
Fletcher-Reeves 共轭梯度法,为共轭梯度法中存储量要求最小的算法
traincgp
Polak-Ribiers共轭梯度算法, 存储量比traincgf稍大,但对某些问题收敛更快
trainscg
归一化共轭梯度法,是唯一一种不需要线性搜索的共轭梯度法
trainbfg
BFGS- 拟牛顿法, 其需要的存储空间比共轭梯度法要大,每次迭代的时间也要多,但通常在其收敛时所需的迭代次数要比共轭梯度法少,比较适合小型网络
trainoss
一步分割法,为共轭梯度法和拟牛顿法的一种折衷方法
trainlm
Levenberg-Marquardt算法,对中等规模的网络来说, 是速度最快的一种训练算法, 其缺点是占用内存较大。对于大型网络, 可以通过置参数mem-reduc 为1, 2, 3,⋯,将Jacobian 矩阵分为几个子矩阵。但这样也有弊端, 系统开销将与计算Jacobian的各子矩阵有很大关系
2.2 改变BP网络模型参数与逼近结果分析
统计数据包括:隐含层层数、神经元个数、训练算法、学习率、最大迭代次数,分别改变这些模型参数,分析对逼近精度的影响,因此给出了如表2-2所示的
表2-2 更改BP神经网络模型参数表
编号
隐含层层数
神经元个数
训练算法
学习率
激活函数
#1
1
10
Trainlm
0.001
Logsig
#2
2
10,10
Trainlm
0.001
Logsig
#3
3
10,10,10
Trainlm
0.001
Logsig
#4
1
20
Trainlm
0.001
Logsig
#5
2
20,10
Trainlm
0.001
Logsig
#6
5
20,20,10,10,5
Trainlm
0.01
Logsig
#7
5
20,20,10,10,5
Trainlm
0.1
Logsig
#8
5
20,20,10,10,5
Trainscg
0.01
Logsig
#9
5
20,20,10,10,5
Trainscg
0.01
Tansig
#10
5
20,20,10,10,5
Trainrp
0.01
Logsig
#11
5
20,20,10,10,5
Traingd
0.01
Logsig
BP神经网络的源码如下所示:
%% BP网络逼近非线性函数源码
%%
clear
clc
close all
%% 数据生成
n = 10000; % 总数据量
% x = 20 * rand(n,1)-10; % x生成
x = linspace(-10,10,n); % x生成
fx = (1 + 3.*x - 2.*x.^2).*exp(-x.^2./2); % fx生成
dataOrigin = [x,fx];% 原始数据生成
%%
figure(1)
plot(x,fx,'LineWidth',2)
grid on
title('原始非线性函数')
xlabel('X Label')
ylabel('Y Label')
%% 拆分数据集
X_train = x(1:8000);
X_test = x(8001:end);
Y_train = fx(1:8000);
Y_test = fx(8001:end);
disp('1*************************************************')
epochs=1000000;
goal = 1e-7;
mid = [20];
transfun = {'logsig'};
stra = 'trainlm';
lr = 0.001;
[netALL] = trainAndModel(X_train,Y_train,epochs,goal,mid,transfun,stra,lr);
% test
SimYALL = sim(netALL,X_test);
% cal score
deltaY = Y_test - SimYALL;
fprintf('最大绝对误差绝对值,即绝对误差限为:')
[MaxindeltaY,p1] = max(abs(deltaY))
deltaToY = deltaY./Y_test;
fprintf('最大相对误差绝对值,即相对误差限为:')
[MaxindeltaToY,p2] = max(abs(deltaToY))
% 均方差MSE
fprintf('均方误差MSE为:')
test_mse = mse(deltaY)
% 和方差SSE
fprintf('和方差SSE为:')
test_sse = test_mse*n
% 均方根RMSE
fprintf('均方根差SSE为:')
test_rmse = sqrt(test_mse)
%%
figure(2)
hold on
plot(X_test,Y_test,'LineWidth',1.5)
plot(X_test,SimYALL,'LineWidth',1.5)
plot(X_train,Y_train,'','LineWidth',1.5)
legend('非线性函数理想曲线','非线性函数BP逼近曲线','训练部分')
title('BP网络训练结果')
xlabel('X Label')
ylabel('Y Label')
grid on
axes('Position',[0.54 0.17 0.34 0.33])
hold on
plot(X_test,Y_test,'LineWidth',2)
plot(X_test,SimYALL,'LineWidth',2)
grid on
axis([6 10 -0.00006 0.0002])
2.2.1 改变隐含层层数
根据表2-2中编号#1、#2、#3的网络模型参数,隐含层层数分别设置为1、2、3层,镁层神经元个数均为10,训练算法为trainlm,学习率为0.001,激活函数为logsig,将均方误差(mse)作为寻优指标,在验证集中进行验证,最终得到性能结果如下所示:
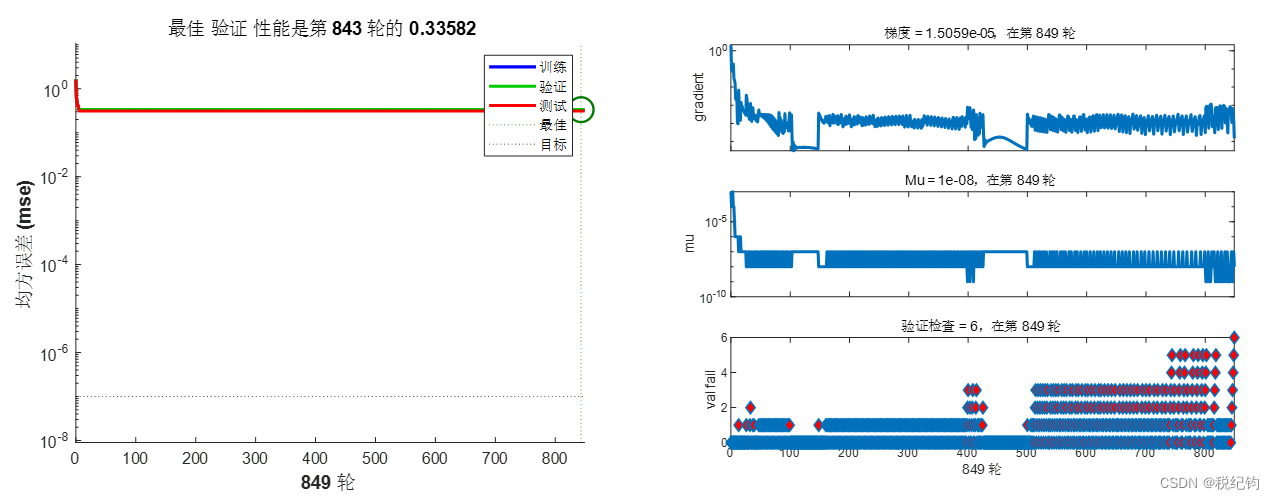
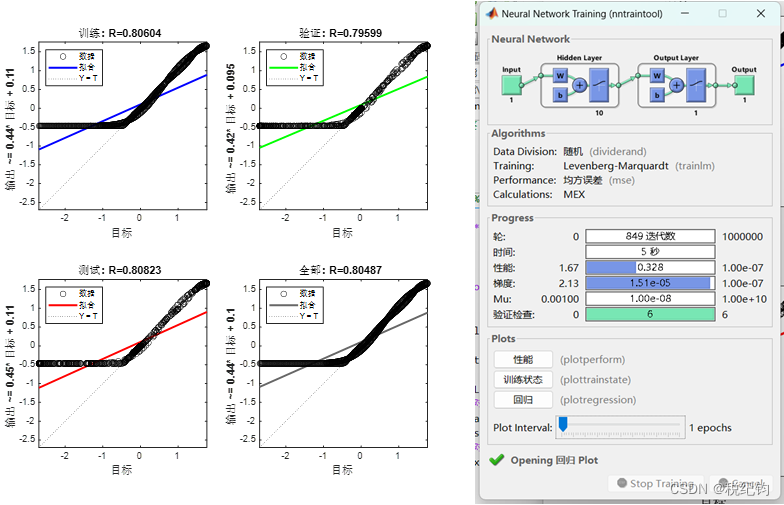
图2-4 #1模型参数训练结果
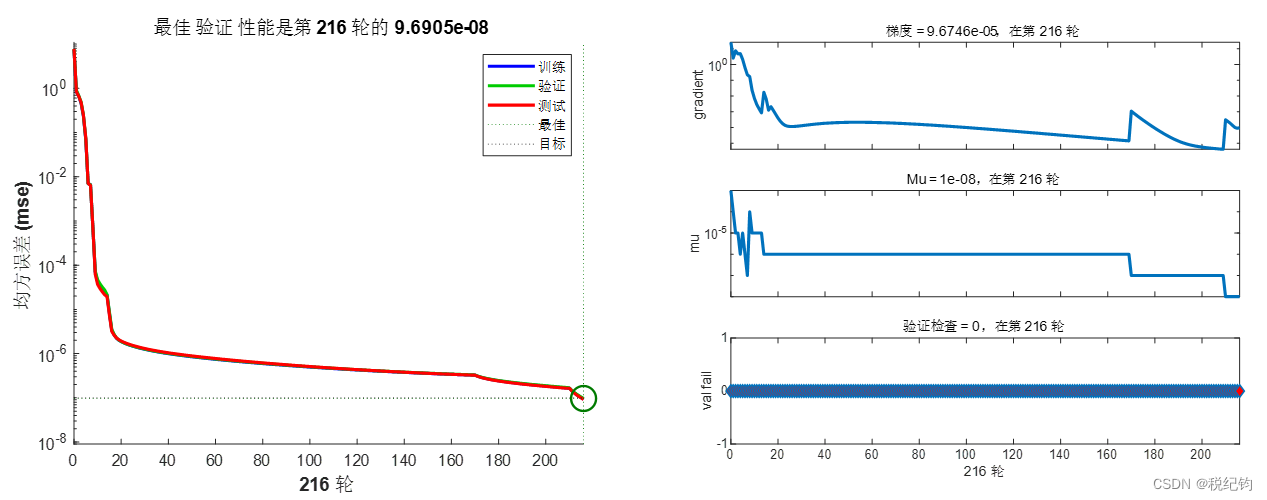

图2-5 #2模型参数训练结果

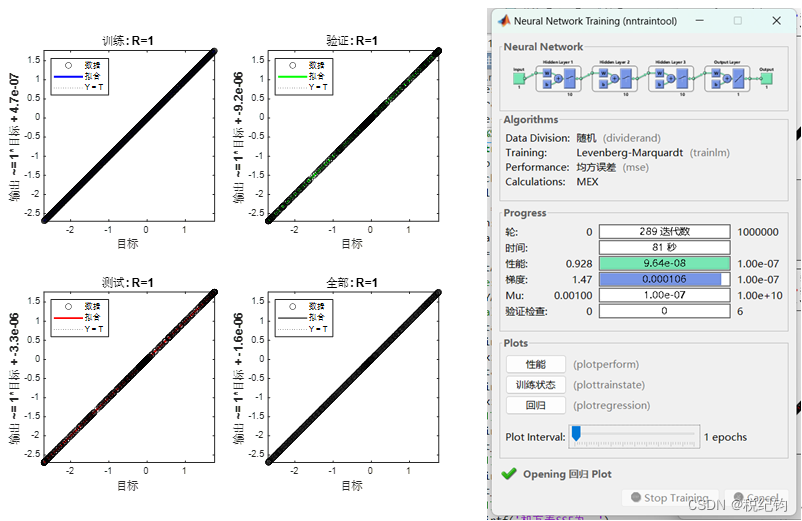
图2-6 #3模型参数训练结果
2.2.2 改变每层神经元个数
如表2-2,针对编号#1,改变神经元个数为20,其他参数不变,可以得到训练结果如图2-7所示。
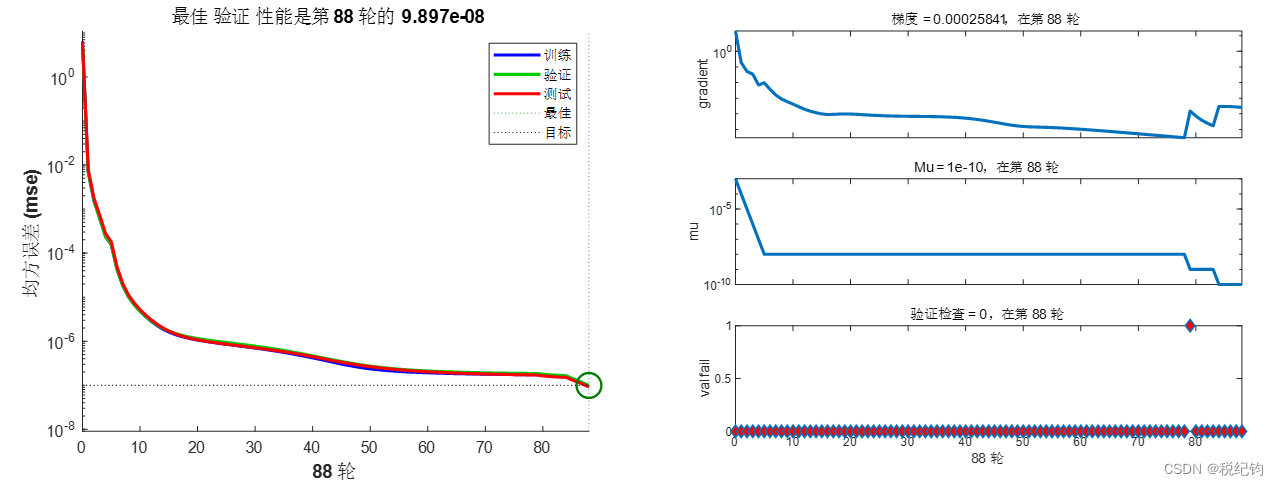
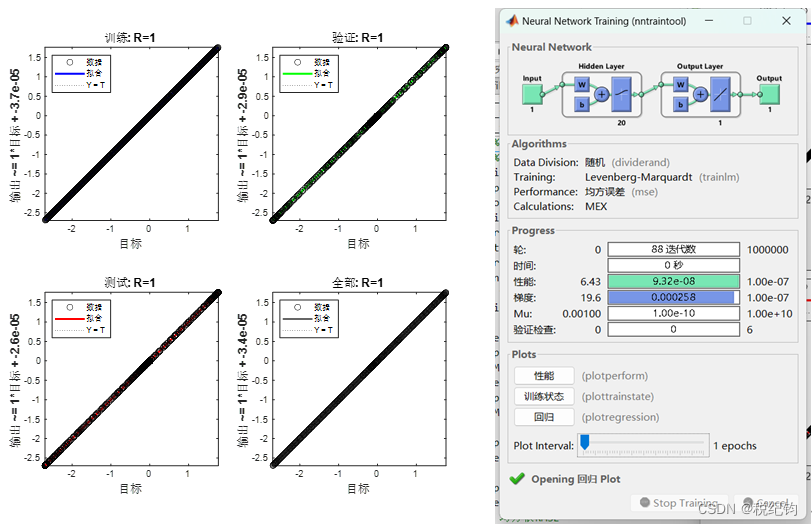
图2-7 #4模型参数训练结果
同理,针对编号#2,仅改变第一层隐含层的神经元个数为20,其他参数不变,可以得到训练结果如图2-8所示。
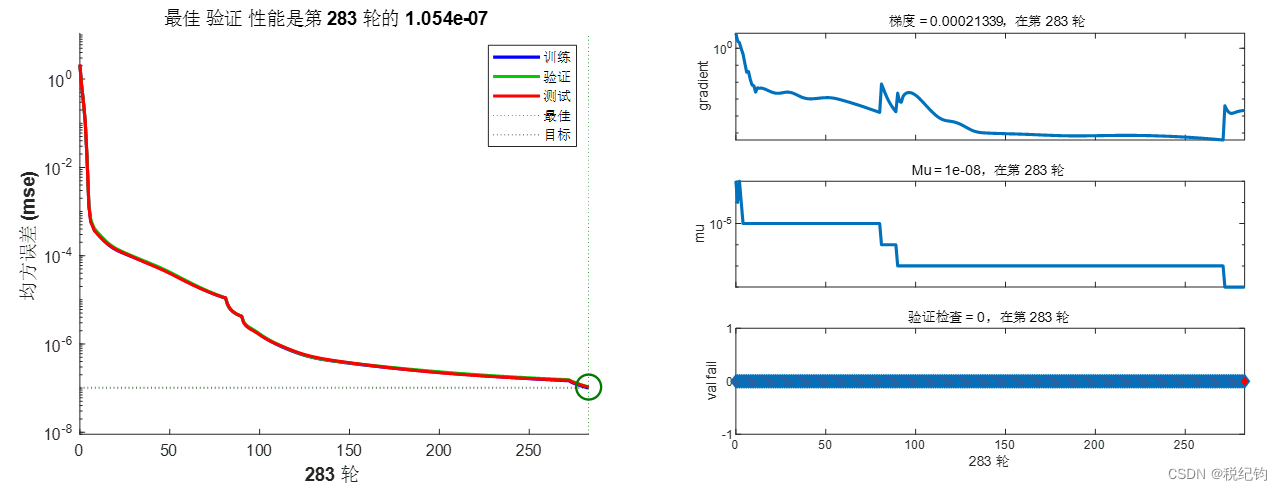
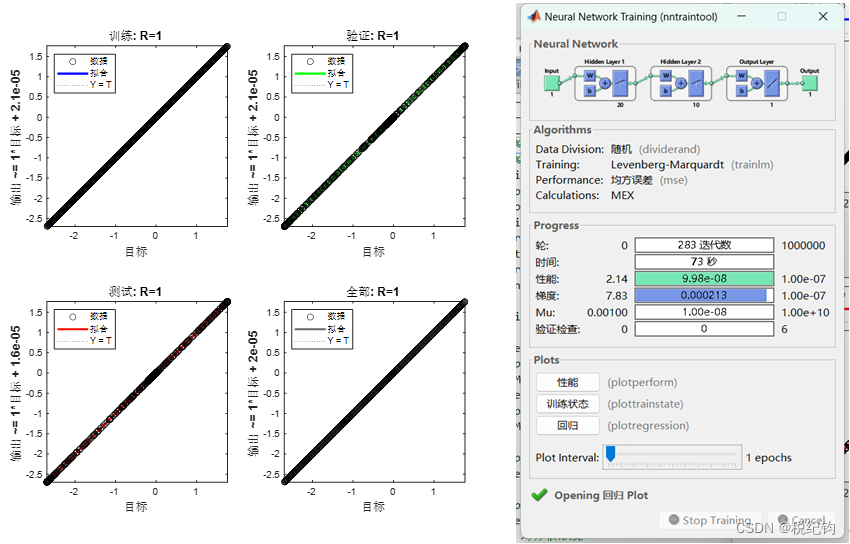
图2-8 #5模型参数训练结果
2.2.3 改变学习率
如表2-2中编号#6、#7所示,隐含层层数设置为5层,神经元个数依次为20、20、10、10、5,学习率分别为0.01、0.1,训练算法与激活函数分别为trainlm、logsig,训练结果如图2-9、图2-10所示。
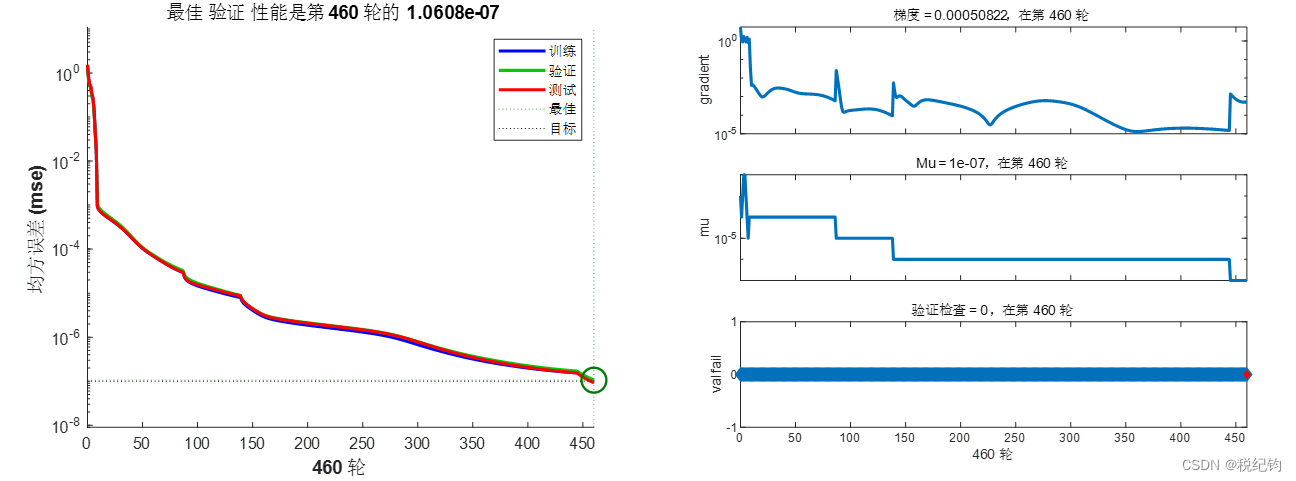
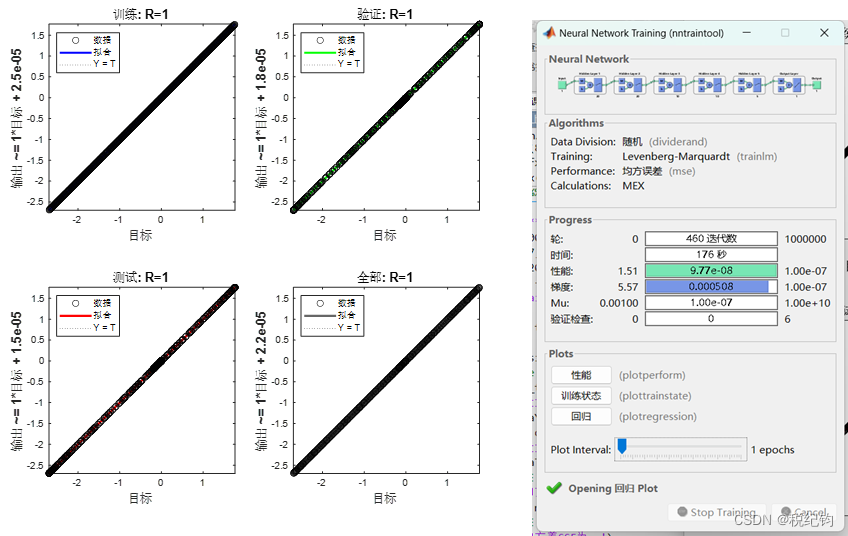
图2-9 #6模型参数训练结果
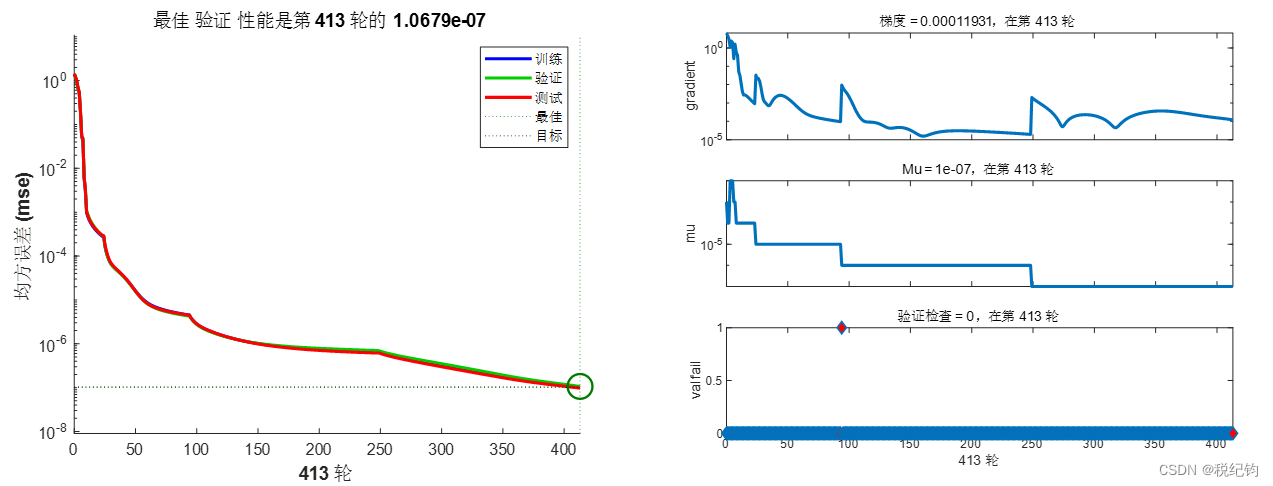
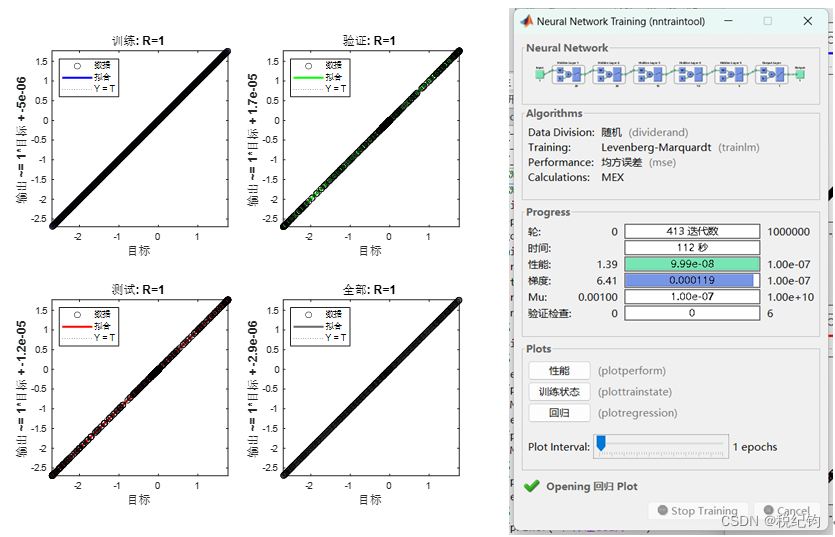
图2-10 #7模型参数训练结果
2.2.4 改变训练算法
如表2-2中编号#6、#8、#10、#11模型参数所示,隐含层均设置为5层,其神经元个数依次为20、20、10、10、5,学习率均为0.01,训练算法分别为trainlm、trainscg、trainrp和traingd,激活函数均为logsig。如表2-1所示,分别使用的是Levenberg-Marquardt算法(对中等规模的网络来说, 是速度最快的一种训练算法)、归一化共轭梯度法(唯一一种不需要线性搜索的共轭梯度法)、弹性BP 算法(具有收敛速度快和占用内存小的优点)以及基本梯度下降法。训练结果如图2-11、图2-13、图2-14所示。
2.2.5 改变激活函数
如表2-2中编号#8、#9模型参数所示,隐含层均设置为5层,其神经元个数依次为20、20、10、10、5,学习率均为0.01,训练算法为trainlm,激活函数分别为logsig、tansig。训练结果如图2-12所示。

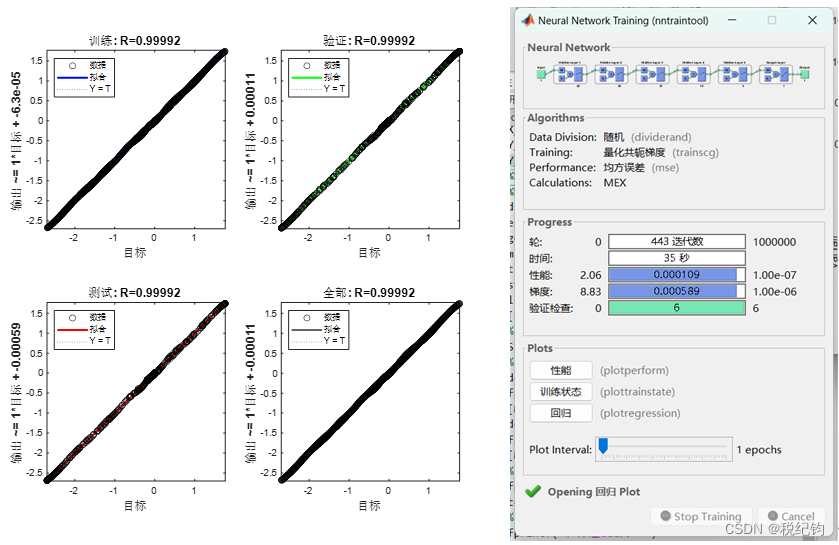
图2-11 #8模型参数训练结果
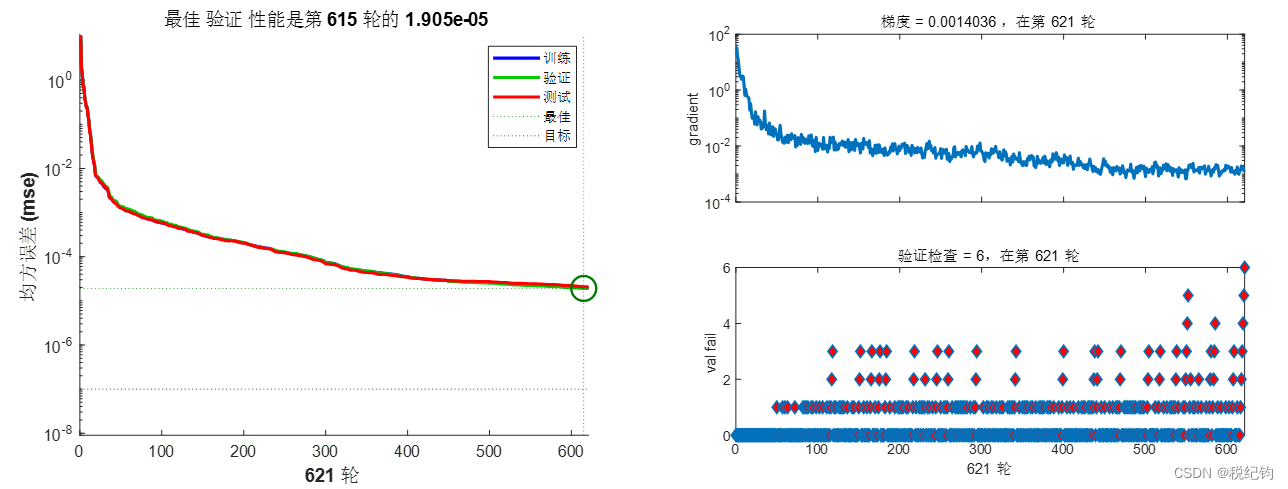
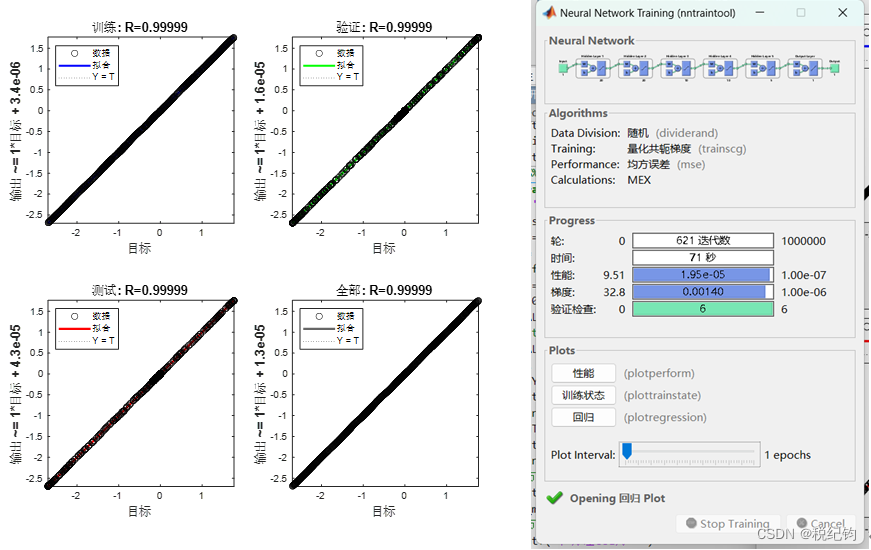
图2-12 #9模型参数训练结果
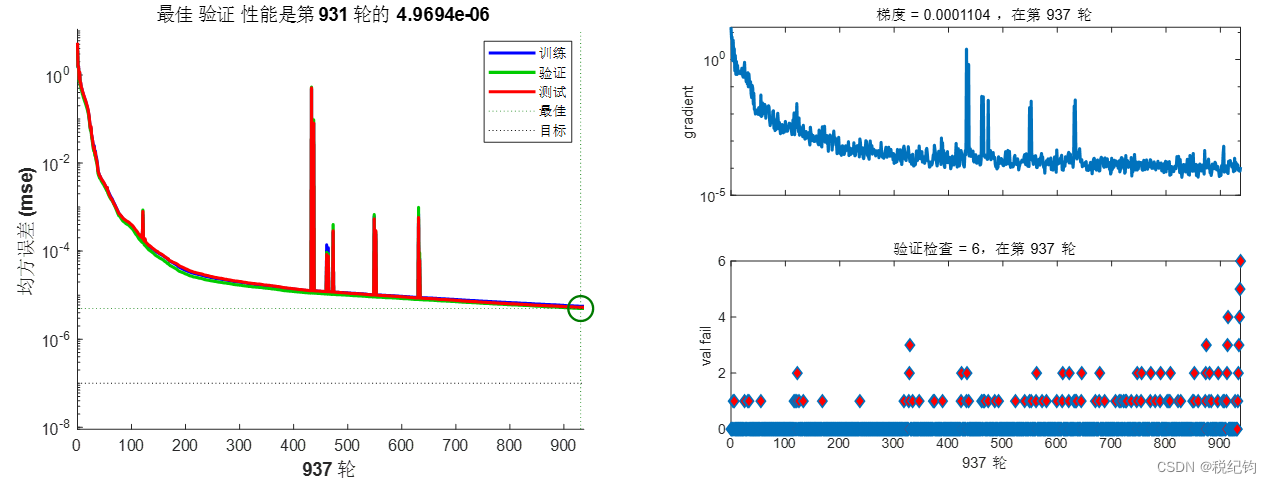
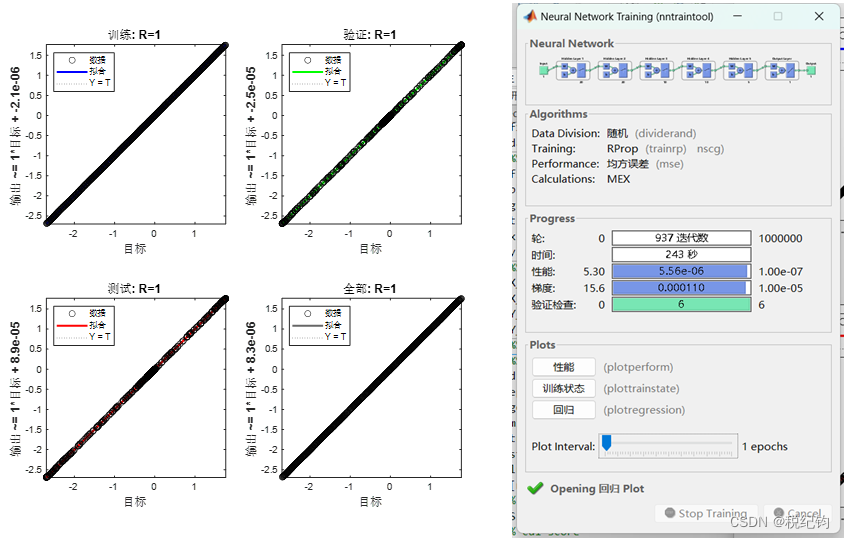
图2-13 #10模型参数训练结果
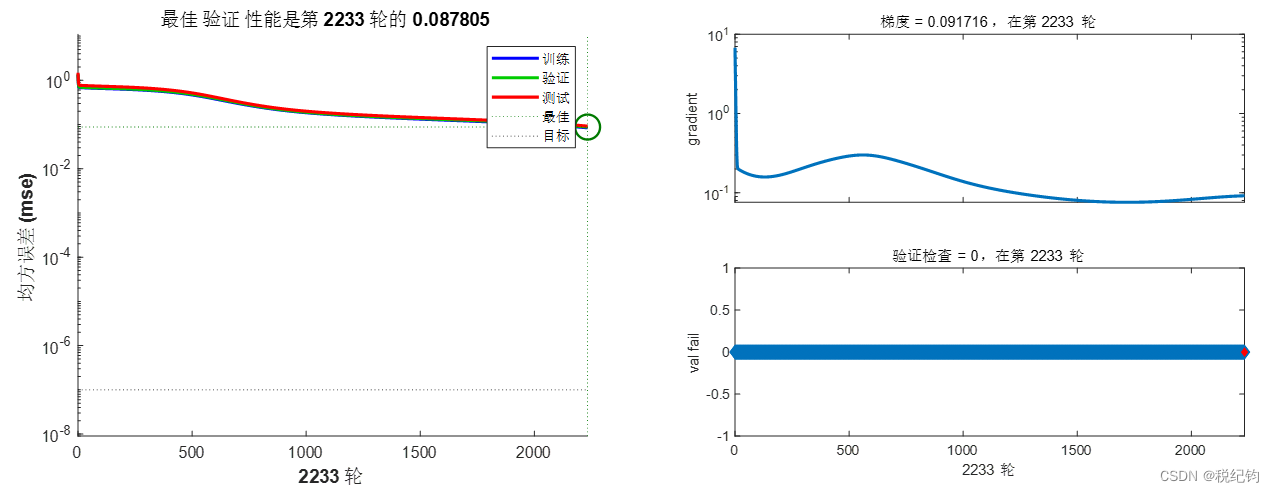

图2-14 #11模型参数训练结果
2.2.6 逼近结果分析
不同BP网络模型参数的迭代次数、训练时长如表2-3所示,MSE、SSE、RMSE以及最大相对误差和最大绝对误差结果如表2-4所示。
表2-3 不同BP网络模型迭代次数与训练时长结果
编号
迭代数
训练时长(秒)
#1
849
5
#2
216
42
#3
289
81
#4
88
不到1
#5
283
73
#6
460
176
#7
413
112
#8
443
35
#9
621
71
#10
937
243
#11
10000+
1000+
表2-4 不同BP网络模型MSE、SSE、RMSE等结果
编号
MSE
SSE
RMSE
最大绝对误差
最大相对误差
#1
0.9255
9255.0110
0.9620
1.7650
5.4148e+19
#2
2.3173e-05
0.2317
0.0048
0.0056
1.4902e+17
#3
1.7493
1.7493e+04
1.3226
1.5567
4.7757e+19
#4
8.3655e-09
8.3655e-05
9.1463e-05
9.1786e-05
2.8150e+15
#5
0.7609
7.6091e+03
0.8723
0.9602
2.9458e+19
#6
0.0486
485.7135
0.2204
0.2393
7.3422e+18
#7
0.0644
644.3497
0.2538
0.2780
8.5292e+18
#8
0.0040
40.4638
0.0636
0.0658
2.0186e+18
#9
0.1512
1.5121e+03
0.3889
0.4072
1.2492e+19
#10
6.0798e-09
6.0798e-05
7.7973e-05
7.8006e-05
2.3931e+15
#11
0.0055
54.8824
0.0741
0.0746
2.2898e+18
综上,性能最好的是编号#10的网络,其MSE为6.0798e-09、SSE为6.0798e-05、RMSE为7.7973e-05,训练时长为243秒,但对比编号#4的网络,其指标与#10相近,但训练时长不到1秒,因此我选择#4的网络作为BP神经网络的最终网络,MSE为8.3655e-09、SSE为8.3655e-05、RMSE为9.1463e-05。最优与次优的BP神经网络模型参数,#4模型:隐含层为1层、神经元个数为20,训练算法为trainlm、学习率为0.001,激活函数logsig;#10模型:隐含层为5层、神经元个数分别为20 20 10 10 5、训练算法为tranrp,学习率为0.01,激活函数为logsig。
最优的BP网络模型训练测试结果如下图所示。
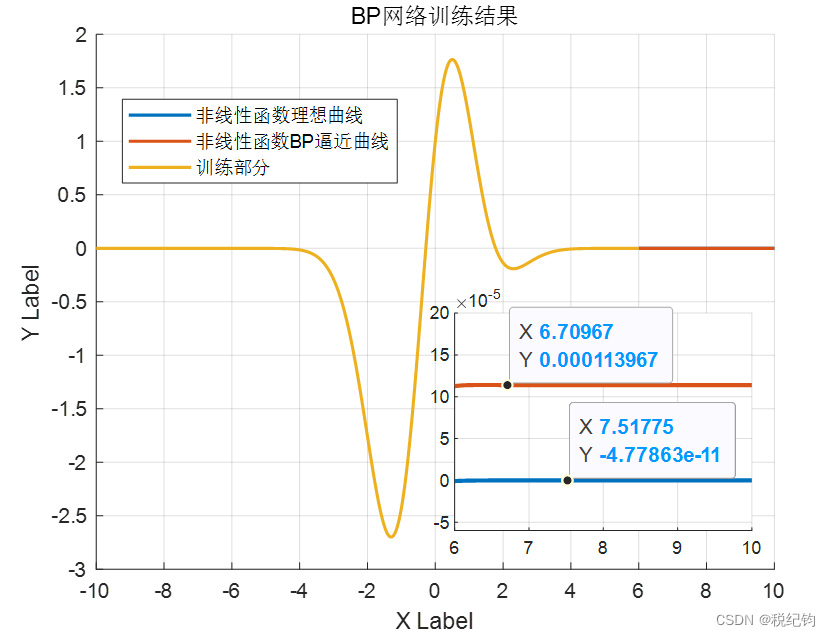
图2-15 最优BP网络模型训练测试结果
2.3 RBF神经网络原理
在上世纪80年代J.Moody和C.Darken提出了神经网络结构模型,也被称作径向基函数网络,在这种结构模型中包含三层前馈神经网络[2]。这种神经网络结构的理论基础是:径向基是作为神经元的隐含基存在的,这些隐含基是构成隐含空间的主要元素,在隐含层可以改变输入的向量,这样就可以实现从低维度到高维度的转变,从而那些在低维度中不能解决的问题在高维度空间中便可以很容易的解决。径向基函数网络在输入和输出上都具有不可比拟的优势,正是得益于这些优势,使得径向基函数在函数逼近、模式识别以及预测等领域得到广泛的应用。
径向基函数网络是三层前馈神经网络,而其中负责接收外界信息的则是输入层,对于由空间层到隐含层的转换则是发生在隐含层,同时在隐含层还能实现非线性的转换。其第三层是起到输出的功能,是输入的最终结果。通过这种网络系统,信息就可以实现从空间层到隐含层,并且在隐含层发生非线性转变,最终以线性的形式传递到输出层。
在径向基函数中,函数是关于中心点对称的,而且对于远离中心点的神经元而言,他们表现出相当低的活性,所以他们随着距离的增加其活性会越来越低。径向基函数有多种形式,但是目前使用最普遍的形式是高斯函数。
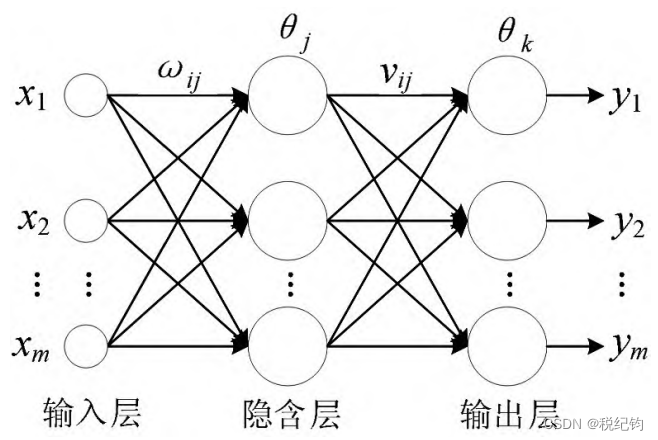
图2-16 RBF神经网络结构
2.4 改变RBF网络模型参数与逼近结果分析
我使用newrb函数来实现。在newrb中,可对如下参数进行调整:
表2-5 newrb参数表
newrb(P, T, goal, spread, MN, DF)
P
输入变量矩阵
T
输出矩阵(标签值)
goal
均方误差的目标
Spread
径向基扩展速度
MN
最大神经元个数,即神经元个数到MN后立即停止训练
DF
每次加进来的网络参数,输出时用
首先确定均方误差目标,为足够拟合非线性函数,应当做到MSE为0,但是为防止过拟合的情况出现,我将goal确定为10^(-16)。改变RBF网络参数如表2-6所示。
表2-6 不同RBF神经网络模型参数
Spread
MN
DF
Spread
MN
DF
Spread
MN
DF
1
26
1
1
10
1
1
90
1
2
26
1
1
14
1
1
90
2
3
26
1
1
18
1
1
90
3
4
26
1
1
22
1
1
90
5
5
26
1
1
26
1
1
90
9
6
26
1
1
30
1
1
90
10
7
26
1
1
38
1
1
90
15
8
26
1
1
50
1
1
90
30
9
26
1
1
70
1
1
90
45
10
26
1
1
90
1
1
90
90
2.4.1 改变径向基扩展速度参数
更改参数径向基扩展速度spread的RBF神经网络源码如下:
%% 更改参数spread的RBF神经网络源码
%% RBF spread
goal_rbf = 1e-16;
spread_rbf = 1;
MN_rbf = 26;
DF_rbf = 1;
SimRBF = zeros(10,2000);
for i = 1:10
netRBF = newrb(X_train,Y_train,goal_rbf,spread_rbf,MN_rbf,DF_rbf);
SimRBF(i,:) = sim(netRBF,X_test);
spread_rbf = spread_rbf + 1;
end
与BP神经网络类似,采用MSE作为目标函数,径向基扩展速度分别设置为:1、2、3、4、5、6、7、8、9、10,spread=1、2、3的RBF神经网络性能曲线如图2-17所示,10种情况的训练结果如图2-18所示。
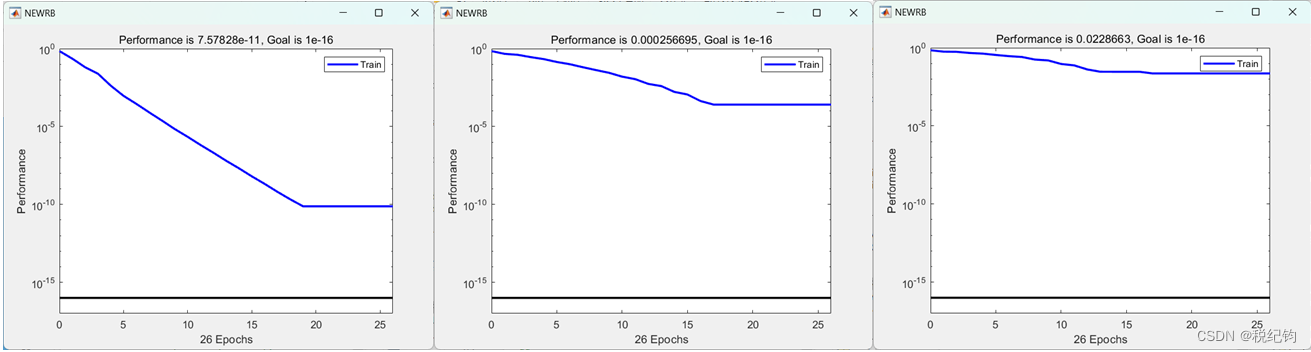
图2-17 spread=1、2、3的RBF神经网络训练MSE曲线
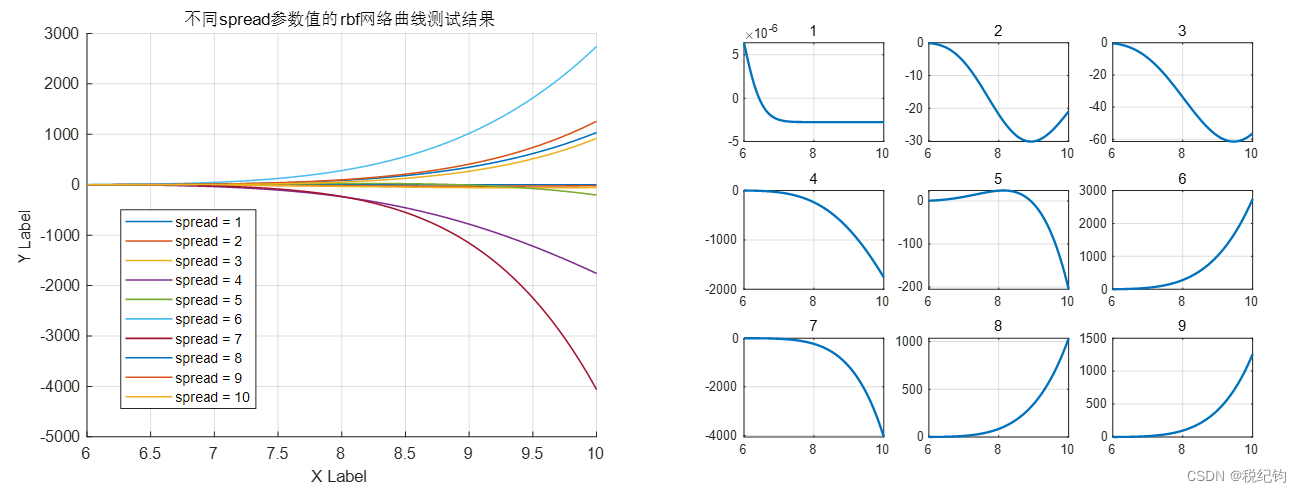
图2-18 不同spread的RBF神经网络测试集非线性函数曲线拟合结果
根据图2-18,非常明显可以观察到,当spread=2、3、4、5、6、7、8、9、10时,结果是发散的,并且仅当spread=1时,mse曲线收敛,因此这里我仅考虑spread=1时的结果作为改变其他参数的径向基扩展速度参数。
2.4.2 改变最大神经元个数参数
更改参数最大神经元个数MN的RBF神经网络源码如下:
%% 更改参数MN的RBF神经网络源码
%% RBF MN
matrix_MN = [10,14,18,22,26,30,38,50,70,90];
spread_rbf = 1;
for i = 1:10
DF_rbf = 1;
MN_rbf = matrix_MN(i);
netRBF_mn = newrb(X_train,Y_train,goal_rbf,spread_rbf,MN_rbf,DF_rbf);
SimRBF_MN(i,:) = sim(netRBF_mn,X_test);
End
最大神经元个数分别设置为:10、14、18、22、26、30、38、50、70、90,MN=50、70、90的RBF神经网络性能曲线如图2-17所示,10中情况在测试集中的结果如图2-20所示。
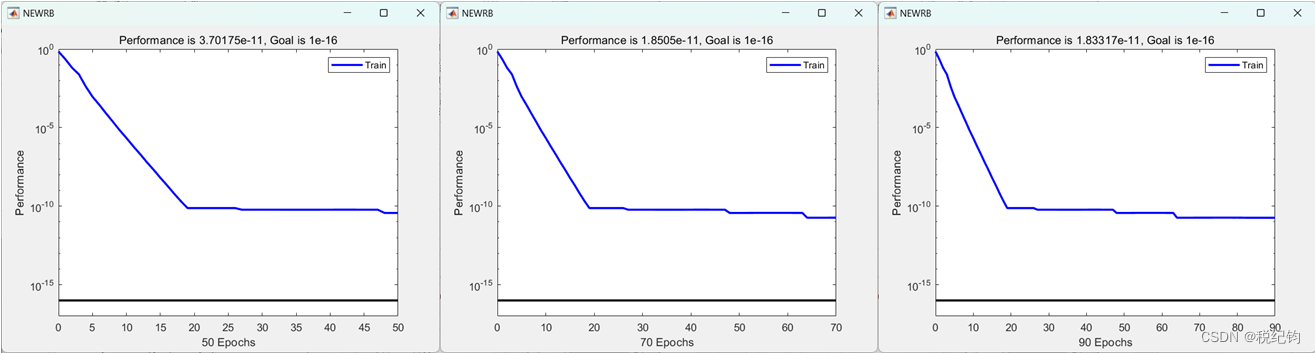
图2-19 MN=50、70、90的RBF神经网络训练MSE曲线
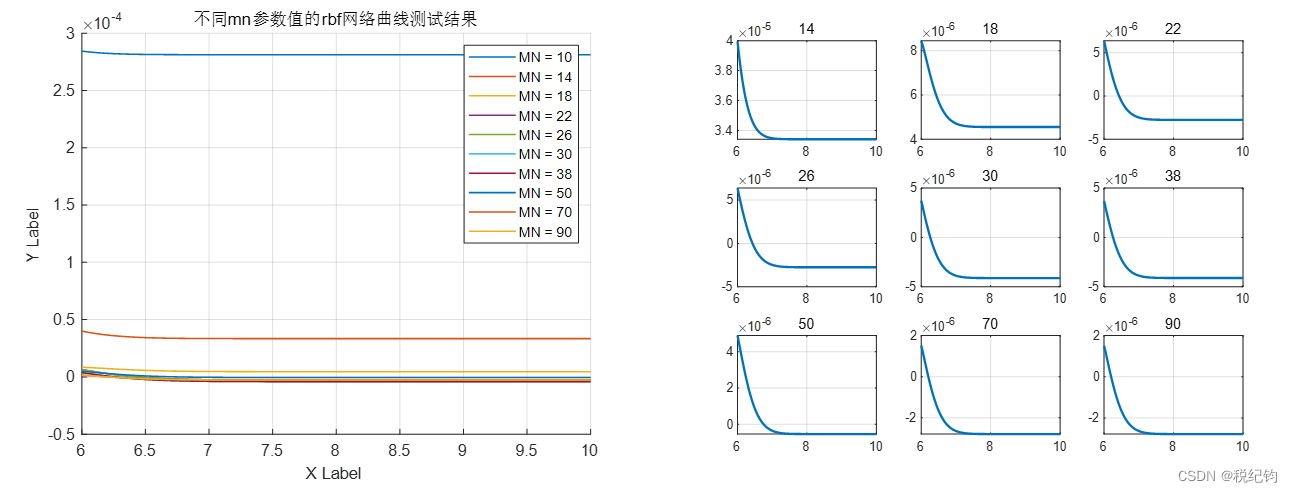
图2-20 不同MN的RBF神经网络测试集非线性函数曲线拟合结果
不同RBF网络模型MSE结果如表2-7,可以观察到,在一定范围内,MN越大,RBF模型性能指标MSE越小,网络越好,且此时最优MN为1,MSE为1.83317e-11。
表2-7 不同RBF神经网络模型MSE结果
MN
MSE
10
2.18221e-06
14
2.07757e-08
18
2.12097e-10
22
7.57382e-11
26
7.57828e-11
30
5.99356e-11
38
5.95365e-11
50
3.70175e-11
70
1.8505e-11
90
1.83317e-11
2.4.3 改变步长参数
选择最大神经元个数MN=90作为最优参数值。最后给定不同的步长DF参数值,分析其对预测结果的影响。更改参数DF的RBF神经网络源码如下:
%% 更改参数DF的RBF神经网络源码
%% RBF DF
for i = 1:10
DF_rbf = matrix_DF(i);
MN_rbf = 1;
netRBF_df = newrb(X_train,Y_train,goal_rbf,spread_rbf,MN_rbf,DF_rbf);
SimRBF_MN(i,:) = sim(netRBF_df,X_test);
end
步长分别设置为:1、2、3的RBF神经网络性能曲线如图2-21所示。
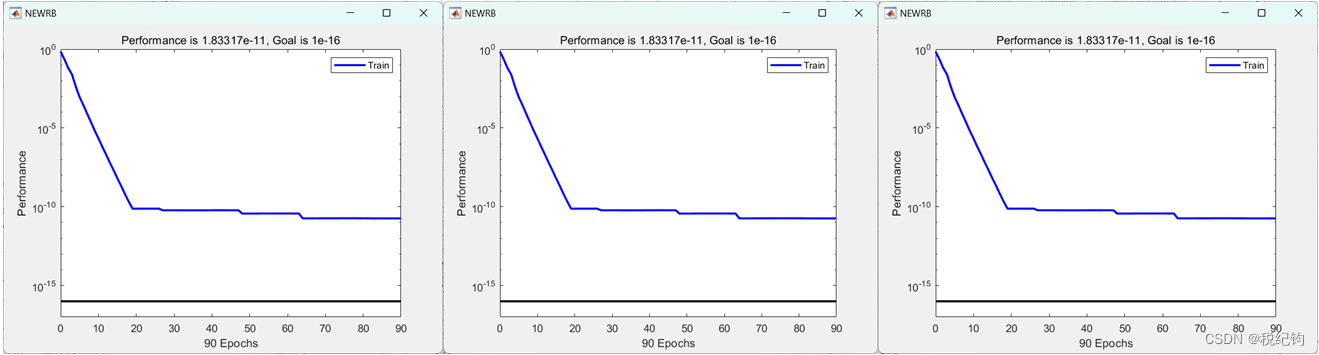
图2-21 DF=1、2、3的RBF神经网络训练MSE曲线
通过上图可以看到,不同的DF对RBF网络训练MSE曲线并没有太大影响,因此本文也将采用DF=1的参数结果为更方便的可视化展示。最终得到最优的RBF网络模型参数:径向基扩展速度spread=1、最大神经元个数MN=90、步长DF=1,图2-22是最优RBF网络模型在测试集中的测试结果。
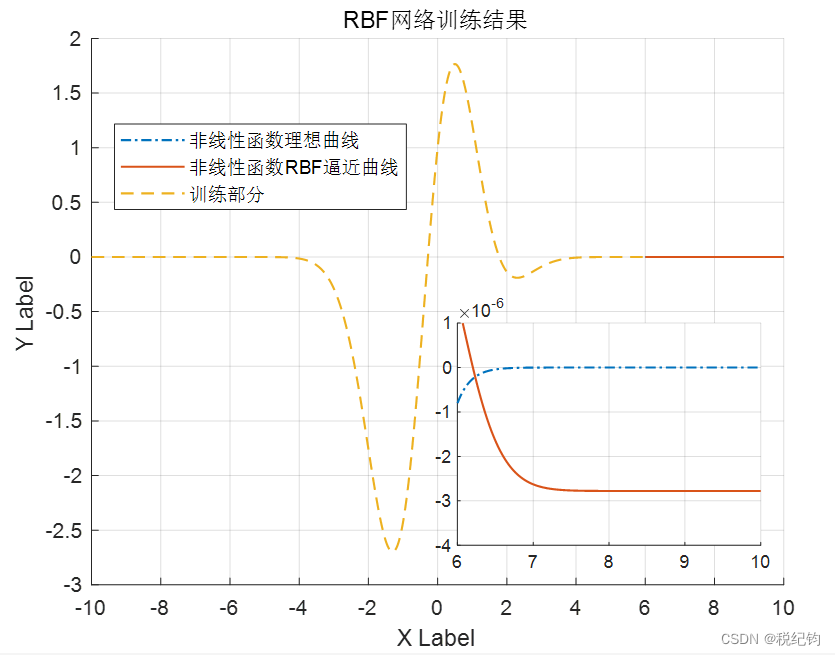
图2-22 最优RBF网络测试集逼近非线性函数曲线
2.5 BP网络与RBF网络逼近结果分析与实验总结
将表现得最优的BP神经网络模型和RBF神经网络模型分别在测试集中进行测试,得到的非线性函数逼近结果如图2-23。
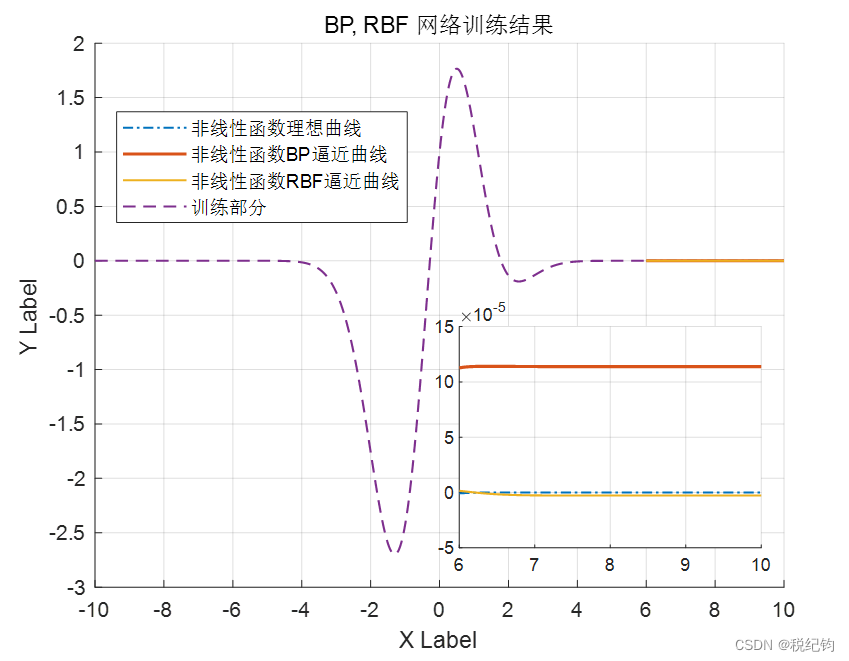
图2-23 最优BP、RBF网络测试集逼近非线性函数曲线比较
结果分析与实验总结
1、RBF 神经网络程序明显比 BP 神经网络简单,训练更加简单。
2、针对该非线性函数逼近问题中,由于问题非常简单,对于最优的BP神经网络和最优的RBF神经网络的训练时间都很短,无法比较两种网络模型的复杂度,因此如果考虑在修改模型参数下,更优的网络模型应该是RBF网络,但实际中,这样的结论还有待讨论,因为BP网络参数还可以更优化。总结两种网络模型特性如下:
A) BP神经网络有如下特性:1.只要有足够多的隐含层和隐层节点,BP网络可以逼近任意的非线性映射关系;2.BP网络的学习算法属于全局逼近算法,具有较强的泛化能力;3.每次样本学习都要重新调整网络的所有权值,收敛速度慢,易陷入局部最小值,不适合实时控制。
B) RBF神经网络有如下特性:1.RBF能人异精度逼近任意连续函数;2.与BP神经网络不同的是,RBF是局部逼近的神经网络;3.RBF从输入到隐层的映射是非线性的,从隐层到输出的映射是线性的,可大大加快速度并避免局部极小值,适合实时控制。
C) BP网络和RBF网络具有如下共性:鲁棒性、自适应性较强,隐层和隐层节点数不确定,即需要根据经验试凑。
3、最终得到最优BP神经网络参数:隐含层为1层、神经元个数为20,训练算法为trainlm、学习率为0.001,激活函数logsig,性能评价指标MSE为8.3655e-09、SSE为8.3655e-05、RMSE为9.1463e-05。最优RBF神经网络参数:径向基扩展速度spread=1、最大神经元个数MN=90、步长DF=1,性能评价指标:MSE为1.83317e-11。
2.6 基于BP、RBF神经网络逼近非线性函数MATLAB源码
基于BP、RBF神经网络逼近非线性函数的源码如下:
%% 基于BP、RBF神经网络逼近非线性函数的源码
%%
clear
clc
close all
%% 数据生成
n = 10000; % 总数据量
% x = 20 * rand(n,1)-10; % x生成
x = linspace(-10,10,n); % x生成
fx = (1 + 3.*x - 2.*x.^2).*exp(-x.^2./2); % fx生成
dataOrigin = [x,fx];% 原始数据生成
%%
figure(1)
plot(x,fx,'LineWidth',2)
grid on
title('原始非线性函数')
xlabel('X Label')
ylabel('Y Label')
%% 拆分数据集
X_train = x(1:8000);
X_test = x(8001:end);
Y_train = fx(1:8000);
Y_test = fx(8001:end);
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% train
disp('1*************************************************')
epochs=1000000;
goal = 1e-7;
mid = [20];
transfun = {'logsig'};
stra = 'trainlm';
lr = 0.001;
[netALL] = trainAndModel(X_train,Y_train,epochs,goal,mid,transfun,stra,lr);
% test
SimYALL = sim(netALL,X_test);
% cal score
deltaY = Y_test - SimYALL;
fprintf('最大绝对误差绝对值,即绝对误差限为:')
[MaxindeltaY,p1] = max(abs(deltaY))
deltaToY = deltaY./Y_test;
fprintf('最大相对误差绝对值,即相对误差限为:')
[MaxindeltaToY,p2] = max(abs(deltaToY))
% 均方差MSE
fprintf('均方误差MSE为:')
test_mse = mse(deltaY)
% 和方差SSE
fprintf('和方差SSE为:')
test_sse = test_mse*n
% 均方根RMSE
fprintf('均方根差SSE为:')
test_rmse = sqrt(test_mse)
%%
figure(2)
hold on
plot(X_test,Y_test,'LineWidth',1.5)
plot(X_test,SimYALL,'LineWidth',1.5)
plot(X_train,Y_train,'','LineWidth',1.5)
legend('非线性函数理想曲线','非线性函数BP逼近曲线','训练部分')
title('BP网络训练结果')
xlabel('X Label')
ylabel('Y Label')
grid on
axes('Position',[0.54 0.17 0.34 0.33])
hold on
plot(X_test,Y_test,'LineWidth',2)
plot(X_test,SimYALL,'LineWidth',2)
grid on
axis([6 10 -0.00006 0.0002])
%% RBF spread
goal_rbf = 1e-16;
spread_rbf = 1;
MN_rbf = 26;
DF_rbf = 1;
SimRBF = zeros(10,2000);
for i = 1:10
netRBF = newrb(X_train,Y_train,goal_rbf,spread_rbf,MN_rbf,DF_rbf);
SimRBF(i,:) = sim(netRBF,X_test);
spread_rbf = spread_rbf + 1;
end
% goal_rbf = 0;
% spread_rbf = 1;
% MN_rbf = 26;
% DF_rbf = 1;
% netRBF = newrbe(X_train,Y_train);
% SimRBF = netRBF(X_test);
%%
figure(3)
hold on
% plot(x,fx)
for i = 1:10
plot(X_test,SimRBF(i,:),'LineWidth',1)
end
grid on
legend('spread = 1','spread = 2','spread = 3','spread = 4','spread = 5','spread = 6','spread = 7','spread = 8','spread = 9','spread = 10')
title('不同spread参数值的rbf网络曲线测试结果')
xlabel('X Label')
ylabel('Y Label')
%%
figure(4)
hold on
for j = 1:9
subplot(3,3,j)
plot(X_test,SimRBF(j,:),'LineWidth',1.5)
grid on
title(j)
end
%% best spread = 1
SimRBF_best_spread = SimRBF(1,:);
%% RBF MN
matrix_MN = [10,14,18,22,26,30,38,50,70,90];
spread_rbf = 1;
for i = 1:10
DF_rbf = 1;
MN_rbf = matrix_MN(i);
netRBF_mn = newrb(X_train,Y_train,goal_rbf,spread_rbf,MN_rbf,DF_rbf);
SimRBF_MN(i,:) = sim(netRBF_mn,X_test);
end
%%
figure(5)
hold on
% plot(x,fx)
for i = 1:10
plot(X_test,SimRBF_MN(i,:),'LineWidth',1)
end
grid on
legend('MN = 10','MN = 14','MN = 18','MN = 22','MN = 26','MN = 30','MN = 38','MN = 50','MN = 70','MN = 90')
title('不同mn参数值的rbf网络曲线测试结果')
xlabel('X Label')
ylabel('Y Label')
%%
figure(6)
hold on
for j = 1:9
subplot(3,3,j)
plot(X_test,SimRBF_MN(j+1,:),'LineWidth',1.5)
grid on
title(matrix_MN(j+1))
end
%% best MN = 70
SimRBF_best_mn = SimRBF_MN(10,:);
%% RBF DF
matrix_DF = [1,2,3,5,9,10,15,30,45,90];
for i = 1:10
DF_rbf = matrix_DF(i);
MN_rbf = 90;
netRBF_df = newrb(X_train,Y_train,goal_rbf,spread_rbf,MN_rbf,DF_rbf);
SimRBF_DF(i,:) = sim(netRBF_df,X_test);
end
%% best DF = 1
SimRBF_best_df = SimRBF_DF(1,:);
%% Compare
figure(7)
hold on
plot(X_test,Y_test,'-.','LineWidth',1)
plot(X_test,SimYALL,'LineWidth',1.5)
plot(X_test,SimRBF_best_mn,'LineWidth',1)
plot(X_train,Y_train,'--','LineWidth',1)
legend('非线性函数理想曲线','非线性函数BP逼近曲线','非线性函数RBF逼近曲线','训练部分')
title('BP, RBF网络训练结果')
xlabel('X Label')
ylabel('Y Label')
grid on
axes('Position',[0.54 0.17 0.34 0.33])
hold on
plot(X_test,Y_test,'-.','LineWidth',1)
plot(X_test,SimYALL,'LineWidth',1.5)
plot(X_test,SimRBF_best_mn,'LineWidth',1)
grid on
axis([6 10 -5*10^(-5) 15*10^(-5)])
人工智能与机器学习课程大作业其他章节内容:一、知识工程基础;三、模糊逻辑;四、函数优化
版权归原作者 税纪钧 所有, 如有侵权,请联系我们删除。