参考:这篇文章总结得很好呀
(6条消息) 目标跟踪中的相关滤波MOSSE、KCF等_mosses和kcf_泠山的博客-CSDN博客
核相关滤波KCF(Kernel Correlation Filter)
核相关滤波算法(Kernel Correlation Filter, KCF)是相关滤波经典跟踪模型,结合回归问题运动模型和观测模型,并通过循环矩阵扩充训练样本,最后基于核方法对目标进行快速检测及定位。KCF 是经典判别式跟踪算法,将目标跟踪问题视为分类问题。
** 首先,提取目标的 HOG 特征;然后,在感兴趣目标区域进行循环密集采样,以此获得大量训练样本对相关滤波分类器进行训练;接着,由相关滤波分类器计算候选区域置信响应图;最后**,根据响应最大点来定位目标 。
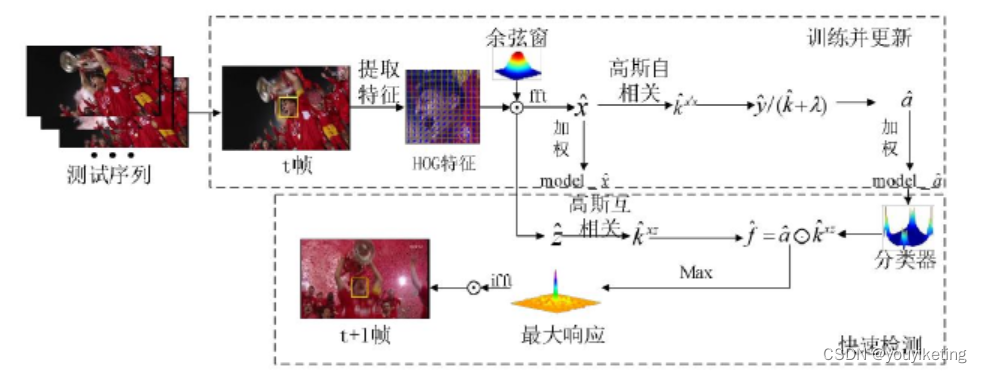
具体步骤如下:
STEP1: 根据初始帧图像信息对目标的位置及大小进行确定;
STEP2: 提取目标区域 HOG 特征,并利用基础样本经过循环移位得到大量训练样本,通过回归模型训练相关滤波模板w。
STEP3: 读取下一帧图像,提取搜索区域图像特征,针对提取得到的特征,采用余弦窗进行相乘平滑计算,得到待检测样本 a;
STEP4: 将待检测样本a与相关滤波模板分类器 w 相乘得响应图f(z) ;
STEP5: 将频域响应图f(z) 通过反傅里叶变换求得时域响应图 ,响应值最大的位置就是最佳预测位置;
STEP6: 对目标的位置进行预测后,根据此位置外观信息,对目标的外观模型以及滤波器模板进行更新;
STEP7: 模型更新完毕之后,利用更新后的滤波分类器模板与后续帧图像搜索区域进行响应运算,对后续帧目标位置进行预测,重复 Step2-Step6,直到所有的视频序列检测完成。
1.岭回归
(6条消息) 【目标跟踪: 相关滤波器 二】岭回归(正则化最小二乘分类器)_岭正则化最小二乘法的期望损失_Kena_M的博客-CSDN博客
**岭回归**是经典线性回归模型,从本质上来说岭回归是基于最小二乘法的改进方法。岭回归通过建立一个成本函数进行模型训练,目的是为了模型性能最优 。


想要求解上述复杂线性方程,一般情况下需要大量繁琐计算,但是核相关滤波算法用到了一种特殊的**循环移位方法**扩充样本,大大降低了计算复杂度。
2.循环矩阵
循环矩阵中每一行元素都是由前一行向量中所有元素依次右移一位获得。
**KCF算法利用循环矩阵扩充训练样本,**其中基样本为正样本,其他都是虚构出的负样本,这样的样本集具有很好的特性,可以很方便的**利用快速傅里叶变换和傅里叶对角化的性质来进行计算**,而不需要得知负样本的具体形式,算法将有关负样本的计算都转换到了频域进行求解。 这样,采用了循环矩阵的性质对输入图像的搜索区域进行密集采样之后,使得进行跟踪器训练时缺少样本的问题迎刃而解。因此,整个 KCF 算法对跟踪器进行训练的目的就是利用生成的这些样本,生成一个滤波器,使得其作用于这些样本时会生成我们期望的分布形式。
因为循环矩阵的特征向量矩阵与其离散傅里叶矩阵维度相同,所以循环矩阵特征值可以用快速傅里叶变换(FFT)求得,以此可以提高算法速度。KCF算法利用循环矩阵扩充训练样本,将计算由时域转换到傅里叶域,避开了矩阵求逆计算,极大提升了算法运行速度。
(6条消息) 【目标跟踪: 相关滤波器 三】循环矩阵_Kena_M的博客-CSDN博客
3.快速核相关检测
考虑实际问题中存在**非线性问题**,对于非线性不可分样本,将其由低维空间映射到高维空间,从高维空间对其进行分类。但是由**低维到高维映射**的过程,往往会出现映射后高维特征空间维数过高的问题,大大增加了计算难度。为了解决这个问题,引入了**核方法**,使最优化问题在高维空间依旧是线性的。

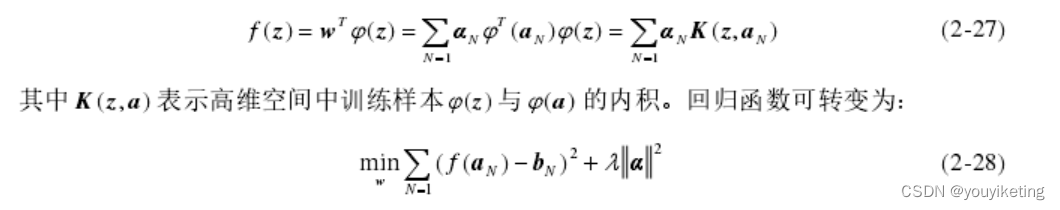


在检测过程中,算法使用已经训练好的跟踪器对padding窗口区域进行滤波计算,得到输出的分布图,将其中**最大响应位置作为预测目标的中心位置**。

4.模型更新

版权归原作者 youyiketing 所有, 如有侵权,请联系我们删除。