相机标定和双目相机标定标定原理推导及效果展示

文章目录

前言

  参考了一些大佬的文章，整理了一下相机标定和双目标定的原理和推导。

一、相机标定

  摄像机成像就是空间场景投影至二维图像平面的空间变换过程。摄像机标定的要解决两个问题:首先确定三维空间点与像素平面像素点间的转换关系，即求解相机内外参;然后确定相机成像过程中的畸变系数，用于图像矫正，因此摄像机标定的参数包括:相机内部参数，外部参数以及畸变参数。
  另外仅仅利用单目相机标定的结果，是无法直接从像素坐标转化到物理坐标的，因为透视投影丢失了一个维度的坐标，所以测距其实需要双目相机。

1.相机的四个坐标系

  相机成像系统中，共包含四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。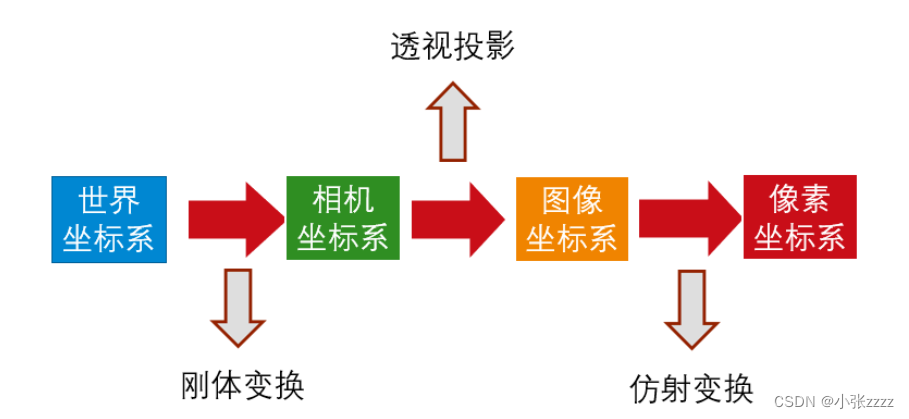

  在一些其他文章中均有说明这四个坐标系分别是什么意思，推荐大家看一下这几位博主的文章，非常有收获。
立体视觉入门指南（1）：坐标系与相机参数
相机标定之张正友标定法数学原理详解（含python源码）
相机标定、双目相机标定（原理）、三维重建效果展示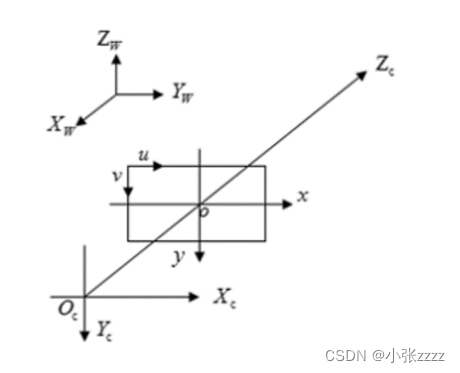
世界坐标系：Xw、Yw、Zw。
相机坐标系： Xc、Yc、Zc。
图像坐标系：x、y。
像素坐标系：u、v。
  其中，相机坐标系的Z轴与光轴重合，且垂直于图像坐标系平面并通过图像坐标系的原点，相机坐标系与图像坐标系之间的距离为焦距f。像素坐标系平面u-v和图像坐标系平面x-y重合，但像素坐标系原点位于图中左上角。

  世界坐标系到像素坐标系转换的全过程：

这里要说明一下几个问题：
1、外参R、T ，也就是世界坐标系到相机坐标系，要6个自由度，除了旋转还要进行平移。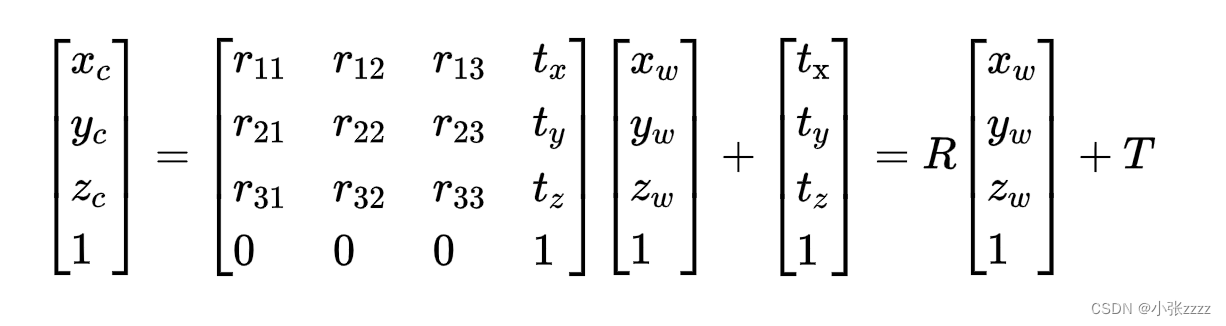

2、s为比例因子（s不为0)，f为有效焦距(光心到图像平面的距离)。相机坐标系转图像坐标系就是等比例缩放的过程。
3、a= f/dX、ay= f/dY，称为u、v轴的尺度因子,M1称为相机的内部参数矩阵，M2称为相机的外部参数矩阵，M称为投影矩阵。

2.相机的畸变

  相机拍摄的图片还存在一定的畸变，畸变包括桶形畸变和枕形畸变。在我的这篇文章中有解释和畸变矫正opencv-python光学畸变校准
径向畸变公式（3阶）如下：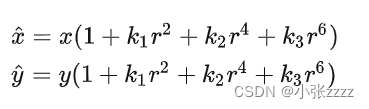

切向畸变公式如下：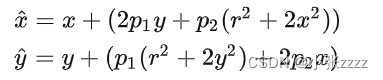

  相机标定的第二个目的就是获得相机的畸变参数，如上式中的K1,K2,K3,P1,P2 等，进而对拍摄的图片进行去畸变处理。

二、张正友标定法

原文我已经帮大家下载好了，直接获取就可以了。链接：https://pan.baidu.com/s/1wp-GmVuc3CTyRXYX1V7aBQ
提取码：8owo

  张正友标定法标定相机的内外参数的思路如下：
1）求解内参矩阵与外参矩阵的积；
2）求解内参矩阵；
3）求解外参矩阵。

1.求解内参矩阵与外参矩阵的积

  张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标 W=0 ，因此，原单点无畸变的成像模型可以化为下式。其中， R1,R2为旋转矩阵R的前两列。为了简便，将内参矩阵记为 A。

注：对于不同的图片，内参矩阵A为定值；对于同一张图片，内参矩阵A，外参矩阵(R1 R2 T)为定值；对于同一张图片上的单点，内参矩阵A，外参矩阵(R1 R2 T) ，尺度因子s为定值。
我们将内参矩阵A和外参矩阵(R1 R2 T)的积记为矩阵H，H即为单应矩阵，则有：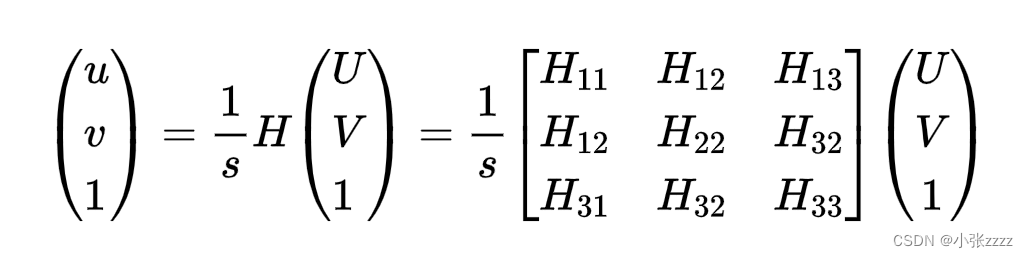

  尺度因子 s可以消掉，这里的H是齐次矩阵，有8个独立未知元素。每一个标定板角点可以提供两个约束方程的对应关系。因此，当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵 。
  以上只是理论推导，在真实的应用场景中，我们计算的点对中都会包含噪声。比如点的位置偏差几个像素，甚至出现特征点对误匹配的现象，如果只使用4个点对来计算单应矩阵，那会出现很大的误差。因此，为了使得计算更精确，一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解，所以实际使用中一般会用其他优化方法，如奇异值分解、Levenberg-Marquarat（LM）算法。

2.求解内参矩阵

  求出来的单应矩阵H是内参矩阵和外参矩阵的混合体，而我们想要最终分别获得内参和外参，所以需要先求内参或者先求外参。先求内参是因为更容易，因为每张图片的内参都是固定的，而外参是变化的。最后求得如下，具体可以参考大佬的推导相机标定之张正友标定法数学原理详解（含python源码）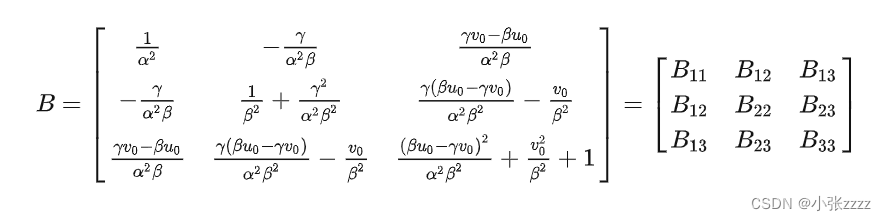

最后可根据对应关系求出结果。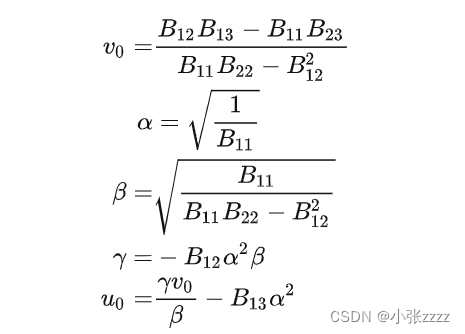

3.求解外参矩阵

  上面我们已经求导了单应矩阵H和内参矩阵A，自然就可以求得每一张图片对应的外参矩阵（R1 R2 T）。
注：这里值得指出，完整的外参矩阵为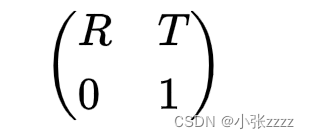
但是，由于张正友标定板将世界坐标系的原点选取在棋盘格上，则棋盘格上任一点的物理坐标W=0 ，将旋转矩阵的R的第三列 R3消掉，因此,R3在坐标转化中并没有作用。但是 要使得 R3满足旋转矩阵R的性质，即列与列之间单位正交，因此可以通过向量 R1,R2的叉乘，即R1 X R2 = R3 ，计算得到R3。

4.标定相机的畸变参数

畸变后的像素坐标为u^v^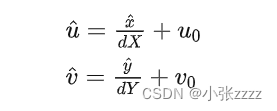



此处也是参考了大佬的推导，建议大家都看一下，非常推荐！

5.双目标定

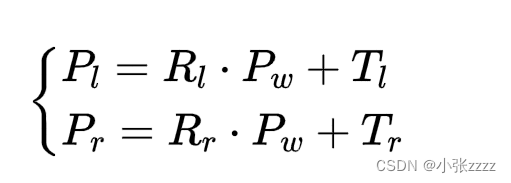
通过 P = R X Pl + T可以推出：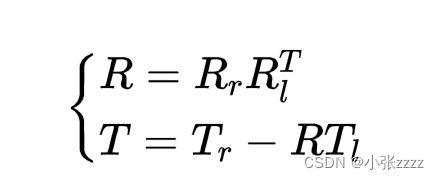

  需要说明的是，无论是Rl、Rr、Tl、Tr，这些在我们单目标定的时候都已经获得过了，opencv单目标定函数中，除了返回我们相机内参、畸变系数外，相机相对于标定物的旋转、平移矩阵也一并返回了，我们可以直接可以用。

6.极线矫正（立体校正）

  之前写的文章里面有介绍极线矫正opencv-python立体匹配（极线校正）
   立体校正的目的就是，利用立体标定所获得的参数将实际非共面行对准的两幅图像，校正成共面行对准。

三、视差图与深度图

引用大佬的文章立体匹配入门指南（8）：视差图、深度图、点云

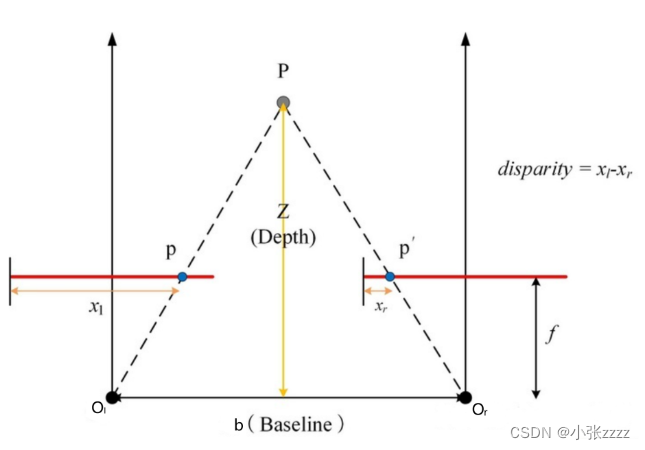
通过三角形相似可得出：

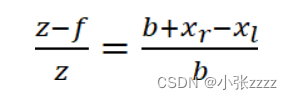
故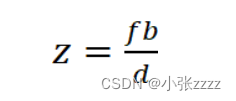

其中,Z为深度,d为视差，b为基线长度，f为焦距（像素单位），xr和xl分别为左右视图主点的列坐标。
注：视差图中存的是视差d，深度图中存的是深度Z。