DataWhale 机器学习夏令营第二期
DataWhale 机器学习夏令营第二期
——AI量化模型预测挑战赛
已跑通baseline,线上得分
0.51138
, 跑通修改后进阶代码,线上得分
0.34497
学习记录一 (2023.08.06)
按照鱼佬直播分享按照以下常见思路分析机器学习竞赛:

1. 问题建模
1.1 赛事数据
数据集情况
给定数据集: 给定训练集(含验证集), 包括10只(不公开)股票、79个交易日的L1snapshot数据(前64个交易日为训练数据,用于训练;后15个交易日为测试数据,不能用于训练), 数据已进行规范化和隐藏处理,包括5档量/价,中间价,交易量等数据(具体可参考后续数据说明)。
预测任务:利用过往及当前数据预测未来中间价的移动方向,在数据上进行模型训练与预测
输入数据:
行情频率:3秒一个数据点(也称为1个tick的snapshot);
每个数据点包括当前最新成交价/五档量价/过去3秒内的成交金额等数据;
训练集中每个数据点包含5个预测标签的标注; 允许利用过去不超过100tick(包含当前tick)的数据,预测未来N个tick后的中间价移动方向。
预测时间跨度:5、10、20、40、60个tick,5个预测任务;
即在t时刻,分别预测t+5tick,t+10tick,t+20tick,t+40tick,t+60tick以后: 最新中间价相较t时刻的中间价:下跌/不变/上涨。
数据分为训练集和测试集,训练集包括
sym0 ~ 9
共
10
个sym从
date0 ~ 63
共
64
天每天上午和下午的数据,测试集则为后续
date64 ~ 78
共
14
天的数据。数据量较大,典型的时间序列预测问题。时间步长为 3 s, 范围从
09:40:03
~
11:19:57
,
13:10:03
~
14:49:57
。
思路:
- 在构建时序特征时需要考虑按照每个上下午,分组进行构造来保证时间步长一致。
- 对10只股票分开处理
- 对5个任务分开处理,
N=5,10为一类,N = 20,40,60一类
数据中缺失值
train_df.isnull().sum()
不存在缺失值
类别和数值特征的基本分布
查看数值型特征在训练集和测试集上的数据分布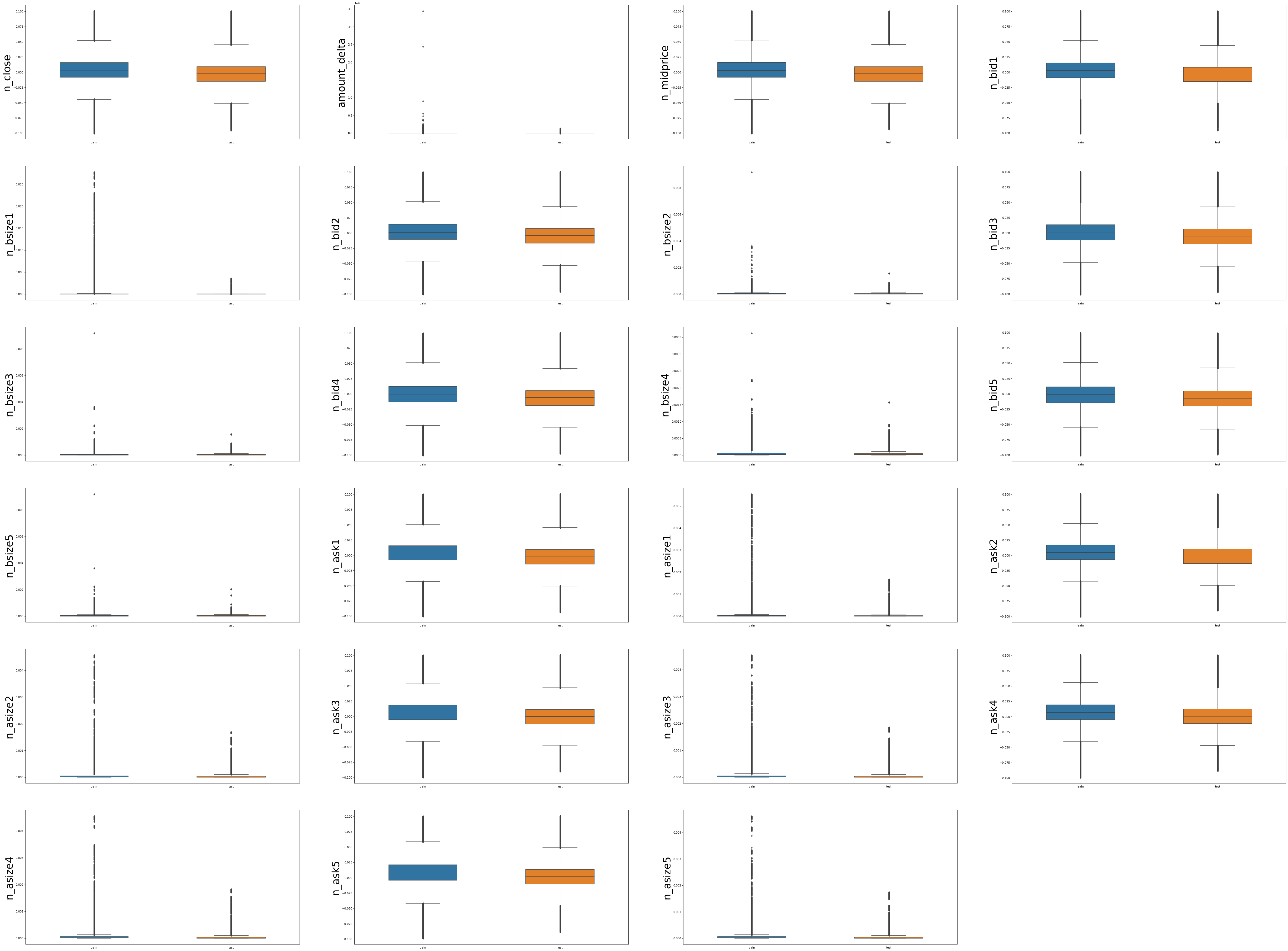
- 价格类数值变量数值比较稳定,训练和测试集分布范围基本一致,如’n_close’,‘n_midprice’, ‘n_bid1’, 'n_ask1’等
- 而和交易量相关的数值变量训练集的变化比测试集较大, 训练集中存在交易量远大于测试集交易量的数据,后续分析可以研究这些高交易量对应的日期是否在一天,是否为特殊时刻,以及是否为异常值
1.2 评价指标
中间价的计算方式
n
_
m
i
d
p
r
i
c
e
=
n
_
b
i
d
1
+
n
_
b
i
d
2
2
n\_midprice = \frac{n\_bid1+n\_bid2}{2}
n_midprice=2n_bid1+n_bid2
其中,一个为0取另一个值
分析:
查看为
n
_
b
i
d
1
,
n
_
b
i
d
2
n\_bid1, n\_bid2
n_bid1,n_bid2中存在0的行:
train_df[(train_df['n_bid1']==0)|(train_df['n_ask1']==0)].index
Index([ 6641, 6642, 6645, 6646, 6647, 6648, 6649, 6650,
6651, 6652,
...
2446840, 2446842, 2446844, 2446845, 2446846, 2446848, 2446918, 2446919,
2446920, 2446921],
dtype='int64', length=175414)
上面为
n
_
b
i
d
1
,
n
_
b
i
d
2
n\_bid1, n\_bid2
n_bid1,n_bid2中存在0的行索引,共175414行存在为0的值。这也说明了之前的箱线图分析中,交易值偏向于低端的原因,因此,后续可以对交易量相关特征进一步分析,包括:1)去除0值观察分布, 2)取对数。
去0后其实对分布影响不大,含0的数据量太少了: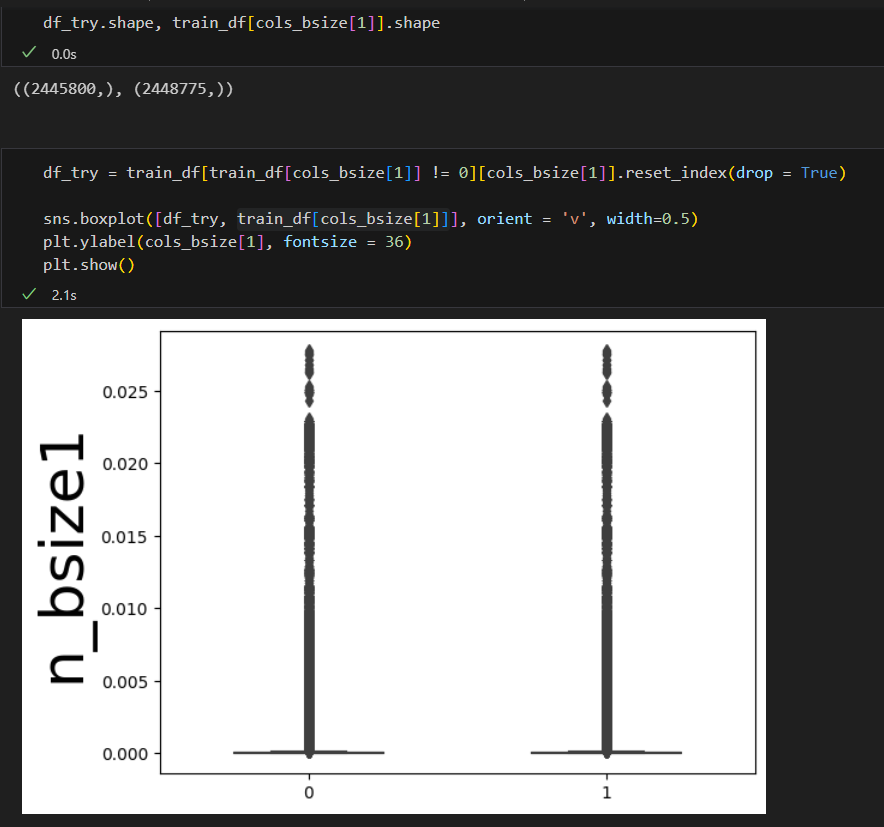
此外,不存在都为0的行,该结果在缺失值分析中已经得到了。
价格移动方向说明
以涨跌幅为基准,分为 2(涨)、1(不变)、0(跌)
L
a
b
e
l
t
N
=
σ
(
n
_
m
i
d
p
r
i
c
e
t
+
N
−
n
_
m
i
d
p
r
i
c
e
t
)
Label_t^N = \sigma(n\_midprice_{t+N} - n\_midprice_t)
LabeltN=σ(n_midpricet+N−n_midpricet)
赛题公式说明
这里我目前还没理解清楚,按照给的公式我去计算了下标签,发现不太一致。另外,如果有了这个具体的指标确定的话不是可以直接用于测试集的计算?
1.3 线下验证
Baseline 采取的是K折交叉验证,时序数据为了保证数据一致性,后续打算采用训练集中
data50~63
共14天数据作为验证集以尽可能保持线上线下一致性,用来分析后续特征工程中衍生特征的好坏。
下一步打算对数据进一步分析,构建交叉特征,同时对不同股票不同天的上下午构建时序特征,对五种不同预测任务构建不同的模型,并采用训练集后14天作为验证集进行验证(K折太久了)。此外,收集些业务信息,感觉对赛题的理解还不够清晰。
PS:
- 一轮赛制,按照目前的排行榜基本无了
- 认真看赛题,两次提交失败都是因为没注意到赛题已经说明 文件详细说明:以zip文件格式提交,编码为UTF-8,文件格式:submit.zip文件,包含文件夹submit
学习记录二(2023.08.09)
2. 特征工程
每次加载和训练模型的速度都太慢了,做了些优化。
- 按照群里的提示把数据存为了 pickle 格式
# 保存为 picklewithopen('train.pickle','wb')as f:
pickle.dump(train_df, f)withopen('test.pickle','wb')as f:
pickle.dump(train_df, f)# 加载 pickle
train_df = pd.read_pickle('train_pickle')
test_df = pd.read_pickle('test_pickle')
- 为了更好的评估特征,只选用了
sym=0第0股的股票的label_5进行线下特征评估。 同时也不采用K折交叉验证,另外考虑时序性的问题,手动划分51-57天数据作为验证集,63天暂时舍去,0-50天作为训练集。
train_df1 = train_df[train_df['sym']==0].sort_values(by =['date','time'])
cols =[f for f in train_df1.columns if f notin['uuid','time','file','label_5','label_10','label_20','label_40','label_60']]
train_df1_train = train_df1[train_df1['date'].isin(train_df1.date.unique()[:-8])]
train_df1_val = train_df1[train_df1['date'].isin(train_df1.date.unique()[-8:-1])]
train_x, train_y = train_df1_train[cols], train_df1_train['label_5']
val_x, val_y = train_df1_val[cols], train_df1_val['label_5']
结合上一次对赛题的一点点理解和和目前的比赛情况(好几个刷到0.99的), 然后我尝试了之前数据探索思考的想法,构建了穿越特征,打算看看有什么效果,线下表现非常好,然后我就在baseline的基础上附加了穿越特征,同时为了更快的得到结果,取消了K折验证。结果刷到
0.99899
… 虽然并没有用到测试集来训练,但本身这种方法也是不符合实际情况的,所以之后还是应该按照正常的特征衍生思路来进行比赛。
收集了些关于时间序列的建模思路:
- 交叉验证:滚动交叉验证
import numpy as np
from sklearn.model_selection import TimeSeriesSplit
X = np.array([[1,2],[3,4],[1,2],[3,4],[1,2],[3,4]])
y = np.array([1,2,3,4,5,6])
time_series = TimeSeriesSplit()print(time_series)for train_index, test_index in time_series.split(X):print("TRAIN:", train_index,"TEST:", test_index)
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
7种交叉验证方法
- 基本规则方法- 加权平均- 指数平滑 时间序列预测:指数平滑法及python实现
- 时间序列模式- 趋势性 - 一阶趋势:构建相邻时间单位的数据差分、比例;- 二阶趋势:反映一阶趋势变化- 周期性 - 环比,将上周期同时期数据作为特征- 构造时间特征,如时间在周期中的位置,距离峰值的时间差- 相关性(自相关):shift平移、历史时刻统计值- 随机性:异常标记 或者 预处理剔除
- 特征提取- 历史平移- 窗口统计- 序列熵特征- 时间特征- 统计特征
版权归原作者 STUffT 所有, 如有侵权,请联系我们删除。