BAB因子(Betting Against Beta)的构建和SAS实证复刻

目录

资源：BAB因子复刻SAS代码

一、引言与综述

早期的实证研究发现，美国股票的证券市场线（SML）与标准CAPM相比更为平坦，这说明风险与收益的关系不能非常很好的满足CAPM。基于此Black et al.（1972）提出了改进版的双因子CAPM模型，即Black CAPM模型：

      E 
     
    
      [ 
     
     
     
       r 
      
     
       j 
      
     
    
      ] 
     
    
      = 
     
    
      E 
     
    
      [ 
     
     
     
       r 
      
     
       z 
      
     
    
      ] 
     
    
      ( 
     
    
      1 
     
    
      − 
     
     
     
       β 
      
     
       j 
      
     
    
      ) 
     
    
      + 
     
    
      E 
     
    
      [ 
     
     
     
       r 
      
     
       m 
      
     
    
      ] 
     
     
     
       β 
      
     
       j 
      
     
    
   
     E[r_j]=E[r_z](1-\beta_j)+E[r_m]\beta_j 
    
   
 E[rj​]=E[rz​](1−βj​)+E[rm​]βj​

相较于原CAPM模型，该模型对美国股市的实证解释能力更强。此外，不少学者从考虑融资约束的CAPM模型角度，讨论了证券市场线的平坦性。Black et al.（1972）的研究开创了研究β和α反向关系的先河。

Frazzini et al.（2014）继承证券市场线更为平坦的观点，从资金限制的角度说明

     α 
    
   
  
    \alpha 
   
  
α 和夏普比率会随着  
 
  
   
   
     β 
    
   
  
    \beta 
   
  
β 的增大而下降。他认为对于使用杠杆受到限制的投资者而言，他们会更倾向于增持高  
 
  
   
   
     β 
    
   
  
    \beta 
   
  
β 股票，这会导致高  
 
  
   
   
     β 
    
   
  
    \beta 
   
  
β 股票相较于低  
 
  
   
   
     β 
    
   
  
    \beta 
   
  
β 股票而言，其风险调整收益更低。基于此，Frazzini et al.（2014）根据股票事前  
 
  
   
   
     β 
    
   
  
    \beta 
   
  
β 的分组构建了BAB因子。该文献提出了5条假设：

(1)股票

     β 
    
   
  
    \beta 
   
  
β 的增大意味着  
 
  
   
   
     α 
    
   
  
    \alpha 
   
  
α 的下降。

(2)BAB因子会产生显著的正收益。
(3)当资金约束收紧时，BAB因子的收益率降低。
(4)资金流动性风险的增加将

     β 
    
   
  
    \beta 
   
  
β 压缩为1。

(5)受约束的投资者更偏好于持有风险较高的资产。

在理论模型构建上，该文献采用了一个代际交叠模型（OLG）对上述5条假设给出解释。OLG模型中包含几种不同类型的代理人。一些代理人无法使用杠杆，因此增持了高贝塔值的资产，导致这些资产的回报率较低。其他代理人可以使用杠杆，但面临保证金限制。不受约束的代理人减持或卖空高贝塔资产，并购买低贝塔资产。上述模型可以推出一条更平坦的证券市场线，斜率取决于代理人之间的平均边际融资约束

     λ 
    
   
  
    \lambda 
   
  
λ ；模型给出某支股票相对于市场的  
 
  
   
   
     α 
    
   
  
    \alpha 
   
  
α 为


  
   
    
     
     
       α 
      
      
      
        t 
       
      
        s 
       
      
     
    
      = 
     
     
     
       ψ 
      
     
       t 
      
     
    
      ( 
     
    
      1 
     
    
      − 
     
     
     
       β 
      
      
      
        t 
       
      
        s 
       
      
     
    
      ) 
     
    
   
     \alpha_{ts}=\psi_t(1-\beta_{ts}) 
    
   
 αts​=ψt​(1−βts​)

高

     β 
    
   
  
    \beta 
   
  
β 对应着  
 
  
   
   
     α 
    
   
  
    \alpha 
   
  
α 的下降；此外，BAB因子的预期超额回报为正：


  
   
    
     
     
       E 
      
     
       t 
      
     
    
      ( 
     
     
     
       r 
      
      
      
        t 
       
      
        + 
       
      
        1 
       
      
      
      
        B 
       
      
        A 
       
      
        B 
       
      
     
    
      ) 
     
    
      = 
     
     
      
       
       
         β 
        
       
         t 
        
       
         H 
        
       
      
        − 
       
       
       
         β 
        
       
         t 
        
       
         L 
        
       
      
      
       
       
         β 
        
       
         t 
        
       
         H 
        
       
       
       
         β 
        
       
         t 
        
       
         L 
        
       
      
     
     
     
       ψ 
      
     
       t 
      
     
    
      > 
     
    
      0 
     
    
   
     E_t(r_{t+1}^{BAB})=\frac{\beta_t^H-\beta_t^L}{\beta_t^H\beta_t^L}\psi_t>0 
    
   
 Et​(rt+1BAB​)=βtH​βtL​βtH​−βtL​​ψt​>0

这从理论上解释了第2条假设。

在实证检验方面，该文献分别在不同的市场中，包括美国和国际股票市场、国债市场、外汇和商品市场等数据，计算根据beta大小分成的10组和BAB因子的超额收益、alpha、beta、年化波动率和年化夏普比率，以检验上述前两条假设。文献后续通过讨论筹资流动性约束（TED利差）对BAB因子收益率的影响，验证第3条假设；通过检验信贷约束更加不稳定时，贝塔系数的横截面离散度较低，验证第4条假设；讨论不同投资者群体的平均事前和事后beta，验证第5条假设。

在本文的复刻工作中，我们重点关注前两条假设的理论构建和在中国A股市场的实证复刻。本文的后续安排如下：第2部分介绍数据处理和复刻细节工作，第3部分给出中国A股市场的实证复刻结果并进行分析，第4部分给出读后感和相关讨论。

二、数据处理和复刻细节

（一）数据来源

本文中的数据来自多个来源。中国A股股票样本包括1990年12月至2022年12月期间CSMAR数据库中所有普通股的数据，包括日度数据和月度数据。因子模型的因子收益率数据来源于中央财经大学金融学院中国资产管理研究中心，时间范围为1994年1月至2022年11月，包括MKT、SMB、HML、UMD、RMW、CMA因子，涵盖FF-3、Carhart-4、FF-5因子模型。市场因子MKT计算方法为全部A股流通市值加权指数，无风险利率采用一年期存款利率。因子收益率数据我们也选取了日度数据和月度数据。

（二）估计事前beta

事前beta的估计我们采用文献的方法，即通过日度数据的定义式进行计算：

        β 
       
      
        ^ 
       
      
     
       i 
      
      
      
        t 
       
      
        s 
       
      
     
    
      = 
     
     
     
       ρ 
      
     
       ^ 
      
     
     
      
       
       
         σ 
        
       
         ^ 
        
       
      
        i 
       
      
      
       
       
         σ 
        
       
         ^ 
        
       
      
        m 
       
      
     
    
   
     \hat\beta_i^{ts}=\hat\rho\frac{\hat\sigma_i}{\hat\sigma_m} 
    
   
 β^​its​=ρ^​σ^m​σ^i​​

通常对beta的估计还可以采用CAPM滚动回归的方法进行估计，很多文献采取的便是回归的方式（如Stambaugh, Liu and Yuan, 2019）。一般而言，回归方法和定义方法是等价的，但是本文献在采用定义法时，分别估计个股、市场的波动率和相关系数，并采取了独特的估计方式。具体而言，本文使用一年滚动数据的标准差估计个股、市场的波动率，使用五年滚动数据估计个股和市场的相关系数，文章声称这样处理是考虑到相关性比波动率变动得更慢。在估计波动率时使用一天的对数收益率，在估计相关系数时使用三天对数收益率：

       r 
      
      
      
        i 
       
      
        , 
       
      
        t 
       
      
      
      
        3 
       
      
        d 
       
      
     
    
      = 
     
     
     
       ∑ 
      
      
      
        i 
       
      
        = 
       
      
        1 
       
      
     
       t 
      
     
    
      ln 
     
    
      ⁡ 
     
    
      ( 
     
    
      1 
     
    
      + 
     
     
     
       r 
      
      
      
        t 
       
      
        + 
       
      
        k 
       
      
     
       i 
      
     
    
      ) 
     
    
   
     r_{i,t}^{3d}=\sum\limits_{i=1}^{t}\ln(1+r_{t+k}^i) 
    
   
 ri,t3d​=i=1∑t​ln(1+rt+ki​)

文章声称这样处理是为了控制非同步交易。同时，文章限制估计波动率时非缺失数据要有至少6个月（120个交易日），估计相关系数时非缺失数据要有至少3年（750个交易日）。

最后，为了减少异常值的影响，遵循Vasicek（1973）等的方法，将β的时间序列估计值收缩为横截面平均值：

        β 
       
      
        i 
       
      
     
       ^ 
      
     
    
      = 
     
     
     
       w 
      
     
       i 
      
     
     
      
      
        β 
       
      
        ^ 
       
      
     
       i 
      
      
      
        T 
       
      
        S 
       
      
     
    
      + 
     
    
      ( 
     
    
      1 
     
    
      − 
     
     
     
       w 
      
     
       i 
      
     
    
      ) 
     
     
      
      
        β 
       
      
        ^ 
       
      
     
       i 
      
      
      
        X 
       
      
        S 
       
      
     
    
   
     \hat{\beta_i}=w_i\hat\beta_i^{TS}+(1-w_i)\hat\beta_i^{XS} 
    
   
 βi​^​=wi​β^​iTS​+(1−wi​)β^​iXS​

为了简单起见，文中并未使用Vasicek（1973）的收缩因子，而是假定在所有时期和所有资产中

      w 
     
    
      i 
     
    
   
     = 
    
   
     0.6 
    
   
  
    w_i=0.6 
   
  
wi​=0.6 且  
 
  
   
    
    
      β 
     
    
      i 
     
     
     
       X 
      
     
       S 
      
     
    
   
     = 
    
   
     1 
    
   
  
    \beta_i^{XS}=1 
   
  
βiXS​=1 。

对个股事前beta的描述性统计可以看出，其中位数为1.068，理论上市场组合的beta值为1，这里较为符合预期。

表1　个股波动率和事前beta描述性统计
变量数目均值标准差最小值中位数最大值个股波动率5339382.88%0.95%0.14%2.75%27.89%个股事前beta5339381.0840.2010.4171.0682.815

（三）构建BAB因子

构建BAB因子的原则是做多低beta资产，并做空高beta资产。这里依然采用Frazzini et al.（2014）的方法，首先进行排序和分组，再进行加权，最后估计BAB因子的收益率。

1.排序和分组

令z为某一支股票上一个月的事前beta从小到大的排名，z越大意味着事前beta越大。例如对于2022年11月，数据集中有3709支股票。农业银行（601288）计算出的事前beta最小，为0.493，所以给农业银行赋予的排名z为1；鹏辉能源（300438）计算出的事前beta最大，为1.573，所以给鹏辉能源赋予的排名z为3709。类似的，我们对1997年2月到2022年11月均进行这样的排序。

按照Frazzini et al.（2014）的方法，每月中排名位于前一半的分入LowBeta组，而排名位于后一半的分入HighBeta组。例如对于2022年11月，z从1到1854的分入LowBeta组，z从1855到3709的分入HighBeta组。之后我们将做多LowBeta组，并做空HighBeta组。

2.加权

通常主流的加权方法为按市值加权，而这里的因子投资组合加权方法较为特别，是rank-weighted加权，即按排名z进行加权。具体而言，对于每个月，取平均排名

       z 
      
     
       ‾ 
      
     
    
      = 
     
     
      
      
        ∑ 
       
       
       
         z 
        
       
         i 
        
       
      
     
       n 
      
     
    
      = 
     
     
      
      
        1 
       
      
        + 
       
      
        2 
       
      
        + 
       
      
        ⋯ 
       
      
        + 
       
      
        3709 
       
      
     
       3709 
      
     
    
      = 
     
    
      1855 
     
    
   
     \overline z=\frac{\sum z_i}{n}=\frac{1+2+\cdots+3709}{3709}=1855 
    
   
 z=n∑zi​​=37091+2+⋯+3709​=1855

对应2022年11月而言，平均排名即为1855。此时HighBeta组和LowBeta组每支个股的权重分别为

       w 
      
     
       H 
      
     
    
      = 
     
    
      k 
     
    
      max 
     
    
      ⁡ 
     
    
      ( 
     
    
      0 
     
    
      , 
     
    
      z 
     
    
      − 
     
     
     
       z 
      
     
       ‾ 
      
     
    
      ) 
     
     
     
     
       w 
      
     
       L 
      
     
    
      = 
     
    
      k 
     
    
      max 
     
    
      ⁡ 
     
    
      ( 
     
    
      0 
     
    
      , 
     
     
     
       z 
      
     
       ‾ 
      
     
    
      − 
     
    
      z 
     
    
      ) 
     
    
   
     w_H=k\max(0,z-\overline z) \\ w_L=k\max(0,\overline z-z) 
    
   
 wH​=kmax(0,z−z)wL​=kmax(0,z−z)

其中归一化系数

     k 
    
   
  
    k 
   
  
k 为（其使得HighBeta组和LowBeta组权重之和为1）

  
   
    
    
      k 
     
    
      = 
     
     
     
       2 
      
      
       
       
         ∑ 
        
        
        
          i 
         
        
          = 
         
        
          1 
         
        
       
         n 
        
       
      
        ∣ 
       
       
       
         z 
        
       
         i 
        
       
      
        − 
       
       
       
         z 
        
       
         ‾ 
        
       
      
        ∣ 
       
      
     
    
   
     k=\frac{2}{\sum_{i=1}^{n}|z_i-\overline z|} 
    
   
 k=∑i=1n​∣zi​−z∣2​

经过这样的加权处理后，我们可以计算得到HighBeta组和LowBeta组的加权收益率和加权beta。

3.估计BAB因子的收益率

根据上一步计算的权重，我们分别计算HighBeta组和LowBeta组的加权收益率和加权beta，并分别依照加权beta的倒数对HighBeta组和LowBeta组做空和做多。可以根据如下公式计算得到BAB因子的收益率

       r 
      
      
      
        t 
       
      
        + 
       
      
        1 
       
      
      
      
        B 
       
      
        A 
       
      
        B 
       
      
     
    
      = 
     
     
     
       1 
      
      
      
        β 
       
      
        t 
       
      
        L 
       
      
     
    
      ( 
     
     
     
       r 
      
      
      
        t 
       
      
        + 
       
      
        1 
       
      
     
       L 
      
     
    
      − 
     
     
     
       r 
      
     
       f 
      
     
    
      ) 
     
    
      − 
     
     
     
       1 
      
      
      
        β 
       
      
        t 
       
      
        H 
       
      
     
    
      ( 
     
     
     
       r 
      
      
      
        t 
       
      
        + 
       
      
        1 
       
      
     
       H 
      
     
    
      − 
     
     
     
       r 
      
     
       f 
      
     
    
      ) 
     
    
   
     r_{t+1}^{BAB}=\frac{1}{\beta_t^L}(r_{t+1}^L-r^f)-\frac{1}{\beta_t^H}(r_{t+1}^H-r^f) 
    
   
 rt+1BAB​=βtL​1​(rt+1L​−rf)−βtH​1​(rt+1H​−rf)

根据构造的做空和做多方法可知，BAB因子的加权事前beta为0。

表2　BAB和MKT因子描述性统计
变量数目均值标准差最小值中位数最大值BAB3101.19%4.13%-9.80%0.77%32.47%MKT3100.95%8.22%-27.14%0.98%36.46%
估计出BAB因子的收益率后，我们进行描述性统计分析。BAB因子收益率均值达到1.19%，超过市场0.95%的平均收益率。此外，我们做出BAB累计收益率和MKT累计收益率进行对比。整体来看，从1997年2月到2022年11月，BAB累计收益率超过了30，远超MKT的累计收益率，初步验证了BAB因子在中国A股市场上的有效性。

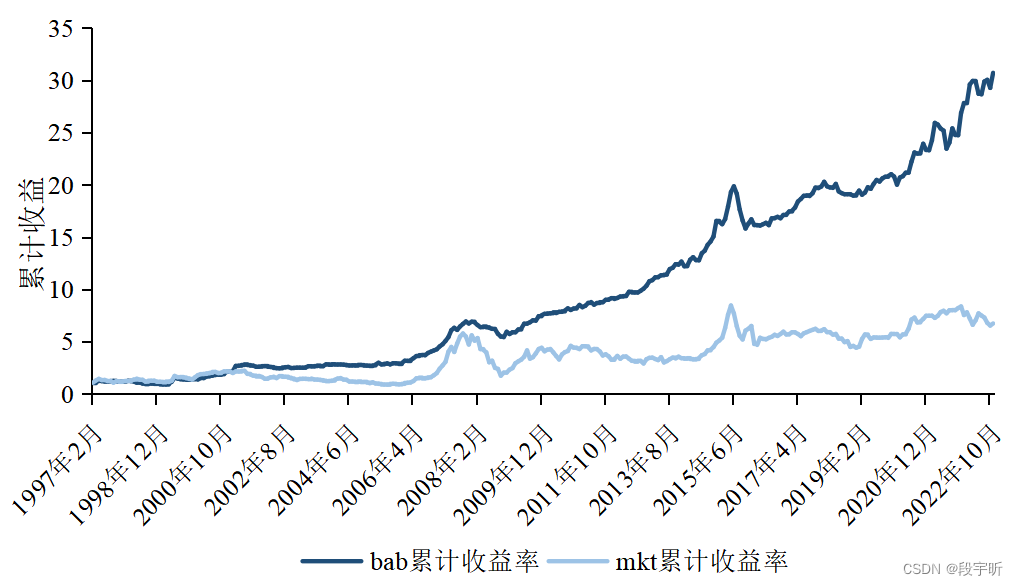
图1　BAB和MKT累计收益率（1997年2月~2022年11月）

三、中国A股市场的实证复刻结果

表3汇报了中国A股市场的实证复刻结果，给出了10个资产组合和BAB因子的相关结果。每个月的资产组合分组是根据上个月底估计的事前beta按升序排列得到，依据A股所有股票的十分位数断点，所有股票被分配到10个投资组合中。BAB因子的分组、加权和构造方式如前文所示，这里不再赘述。

个股收益率数据源于CSMAR数据库在1990年12月至2022年12月期间的所有数据，因子数据来源于中央财经大学金融学院中国资产管理研究中心，时间范围为1994年1月至2022年11月。由于需要滚动估计beta，最终我们得到的投资组合和BAB因子的时间区间为1997年2月至2022年11月。

图2给出了复刻结果中的相关变化情况。作为对比，我们给出了基于美国市场的原论文的表4和图3。

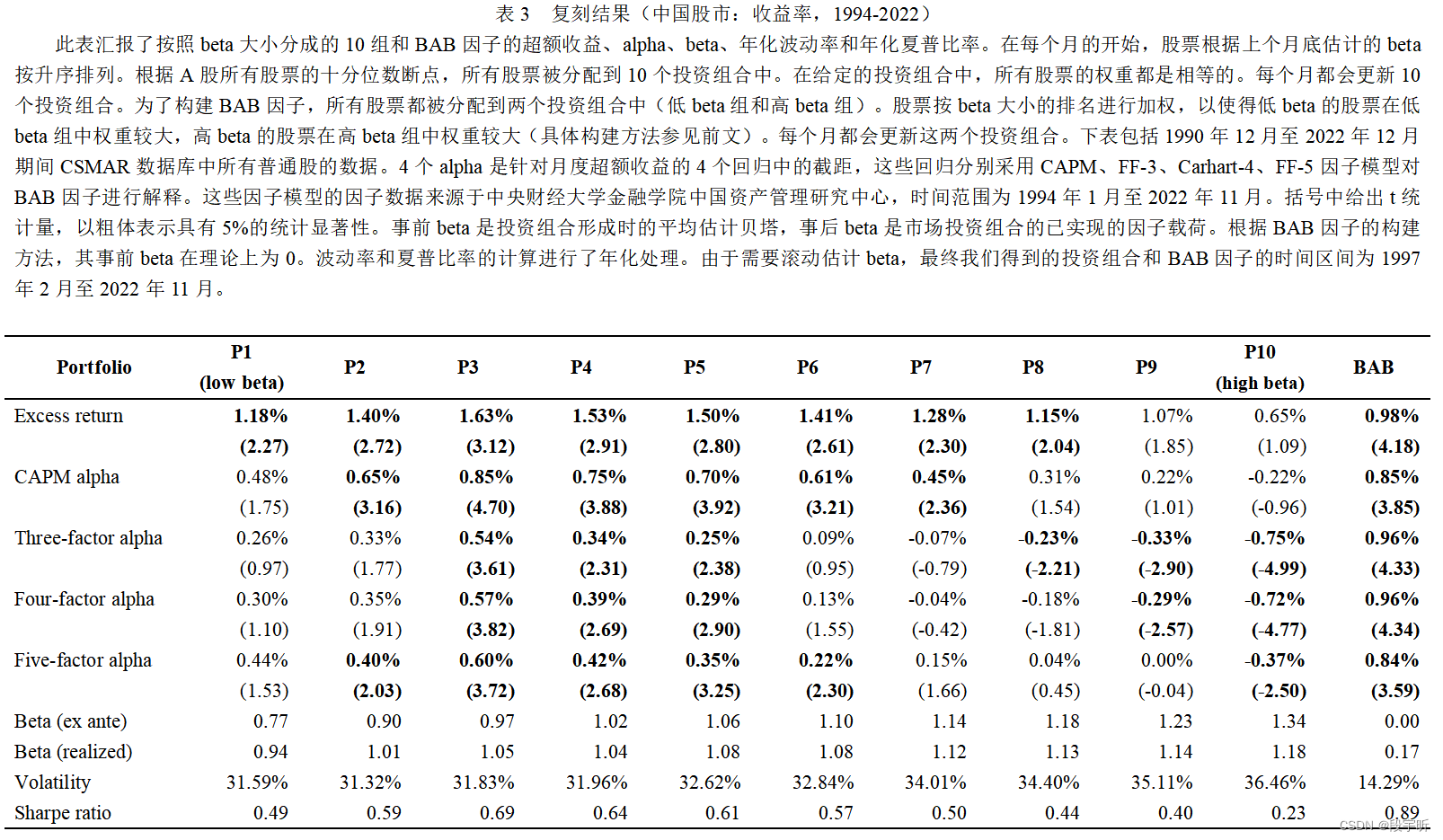
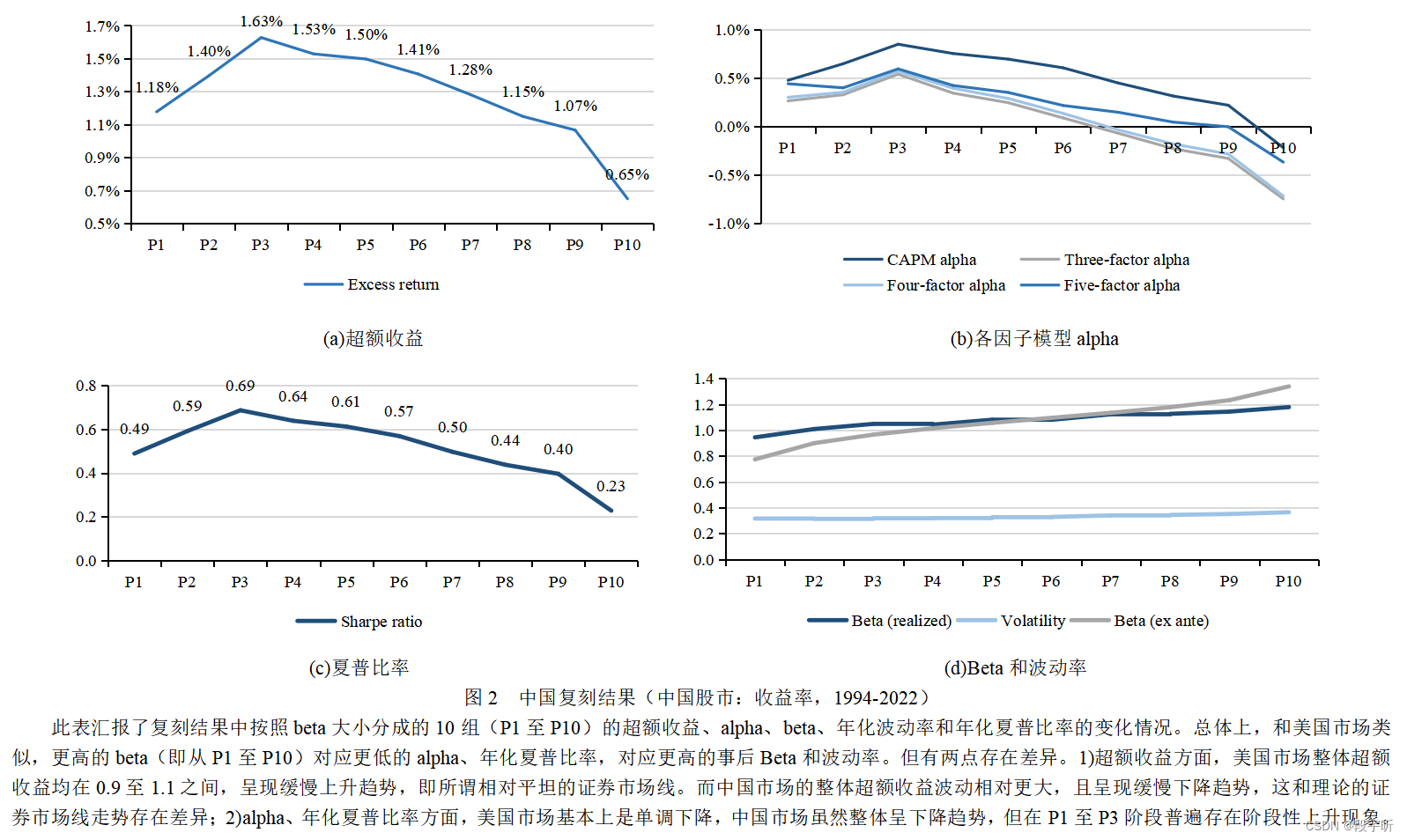
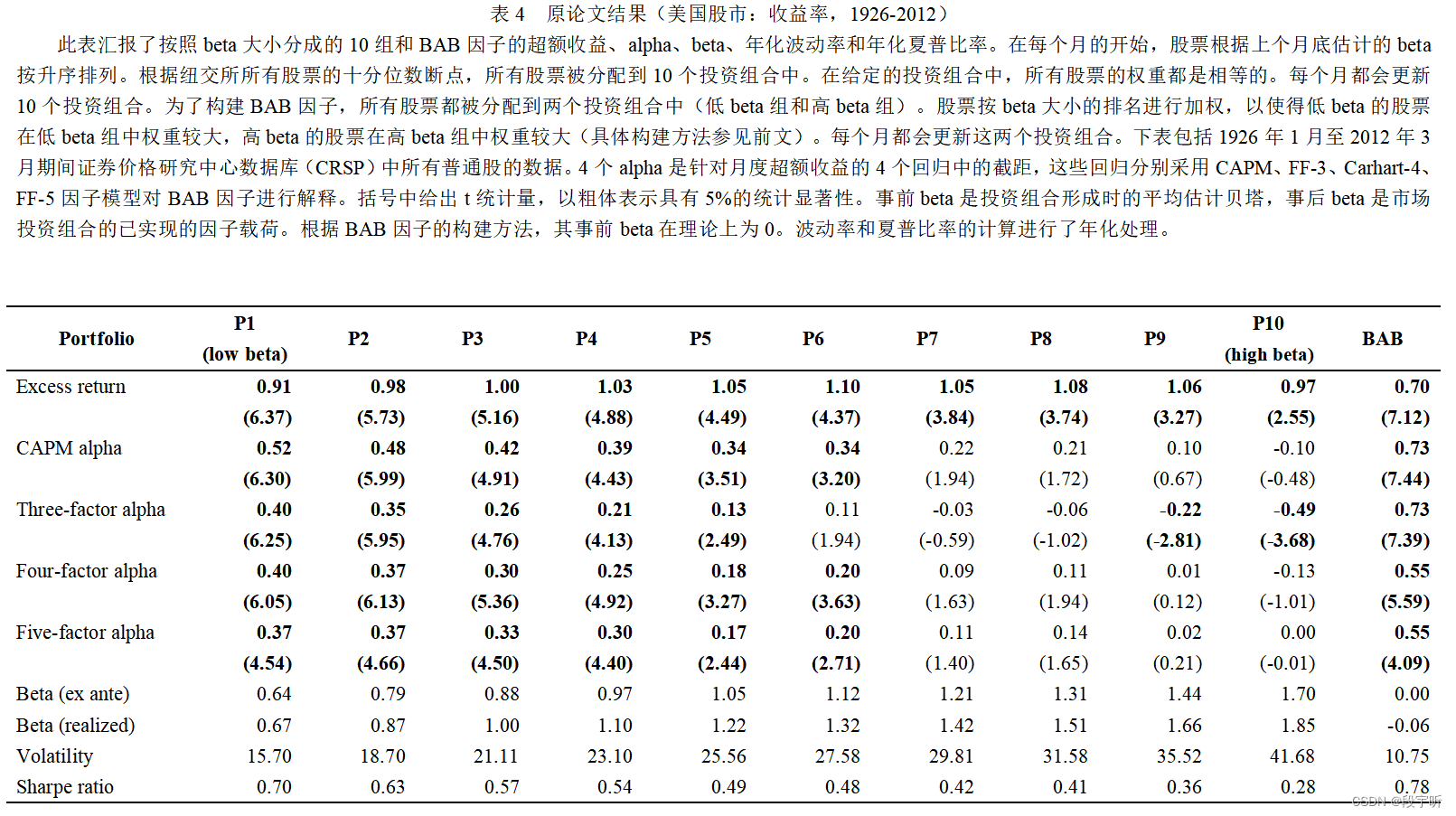
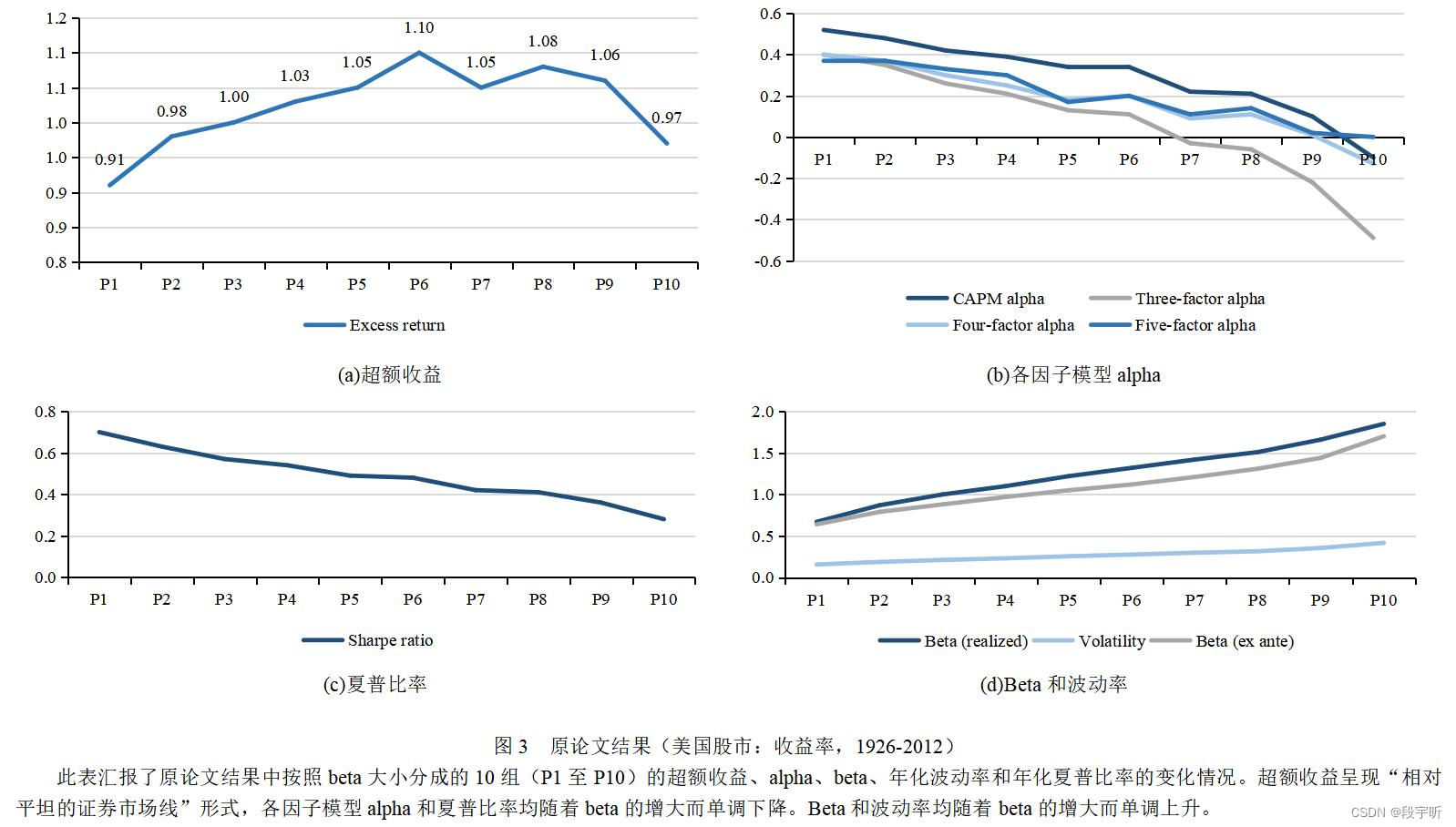
从复刻结果可以看出，和美国市场类似，中国A股市场给出的10个投资组合的平均回报率差异不大。在对CAPM、FF-3、Carhart-4、FF-5因子模型的alpha分析中，与文中假设（1）和Black et al.（1972）的研究一致，低beta投资组合（P1至P5组）中的alpha普遍要高于高beta投资组合（P6至P10组）。此外，夏普比率从低贝塔投资组合到高贝塔投资组合整体呈现下降趋势。而事前、事后Beta和波动率随着beta的增大而增大，这符合预期。

综合以上结果，我们认为假设（1），即“股票β的增大意味着α的下降”在中国市场也成立。值得指出的是，中国市场的结果和原论文美国市场的结果存在如下的明显差异：

（1）超额收益方面，美国市场整体超额收益均在0.9至1.1之间，呈现缓慢上升趋势，这就是所谓相对平坦的证券市场线。而由图2（a）所示，中国市场的整体超额收益波动相对更大（最小为0.65，最大达到1.63），且呈现缓慢下降趋势，这和理论上的证券市场线走势存在差异；

（2）alpha和年化夏普比率方面，美国市场各因子模型alpha和夏普比率均随着beta的增大而单调下降。而中国市场虽然整体呈下降趋势，但各因子模型alpha和夏普比率在P1至P3阶段普遍存在阶段性上升现象，如图2（b）所示。

（3）统计显著性方面，美国市场在前5个投资组合（P1至P5）中，对于所有因子模型的alpha均有5%的显著性（即使P6至P10的显著性不太好）。而中国市场的P1和P2的alpha显著性不好。

（4）在beta方面，中国和美国市场的事前、事后beta均随着beta的增大而增大，但是存在细微差别。10个分组均是通过事前beta进行的，而我们看到中国市场中，从P1到P10的事后beta的变动不及事前beta的变动，而美国市场中事后beta的变动和事前beta的变动幅度相当。

我们推测，上述现象的成因可能是对中国市场分组方法导致的。原文根据纽交所的十分位数进行断点，再对所有的股票进行分组。因为纽交所的股票类型相对丰富，这样的分组方法会避免在某一个组中的股票相互之间差异过小（比如都是小盘股）。但是在中国市场这种效应可能相对较小，而且基于数据可得性，我们是直接对A股所有股票进行十分位数断点，所以在分组效果上可能不如美国市场进行的分组。

之后，我们分析了BAB因子在超额收益、alpha、beta、年化波动率和年化夏普比率上的表现。中国市场的BAB因子超额收益率达到0.98%，并且有4.18的t值。在CAPM、FF-3、Carhart-4、FF-5因子模型下，其截距alpha分别为0.85%、0.96%、0.96%、0.84%，且t值均大于3。这意味着BAB因子获得的超额收益率不能被CAPM、FF-3、Carhart-4、FF-5因子模型很好的解释，所以中国市场的BAB因子是有意义的。

我们同样对中国的BAB因子和美国的BAB因子进行了对比。我们发现美国BAB因子的超额收益和alpha的t值普遍比中国市场要高，甚至能超过7。这意味着已有因子模型对BAB的解释能力在美国更弱，美国市场的BAB因子有效性更好。我们考虑到原文的表4，这是对国际范围内的股票市场进行的讨论，其BAB因子的超额收益和alpha的t值和中国市场类似，甚至表现还不及中国市场。总而言之，我们认为中国市场的BAB因子表现尚可。

四、读后感和相关讨论

经典CAPM模型认为，股票的期望收益水平由市场风险完全决定，高风险意味着高收益。这在理论上表明做多高beta股票、做空低beta股票能获得超额收益。而从Black et al.（1972）开始的一系列的研究却对CAPM的有效性提出了质疑，高风险和高收益之间并不是这样显著相关，而做多高beta股票、做空低beta股票在很多市场会得到负的异常收益。很多学者也发现了这个现象，研究了这个异象可能的解释。Frazzini et al.（2014）指出受杠杆约束的投资者会做多高beta股票，从而降低高beta股票的超额收益。这对于beta异象的成因和机理解释做出了很大贡献。

Fama et al.（1992）指出在剔除和size相关的因素后，beta并不能很好的解释收益率，而规模因子和价值因子的解释能力更好。在这之后，相关学者提出了引入动量因子的Carhart四因子模型，以及在FF-3因子模型基础之上的FF-5因子模型。

Stambaugh et al.（2019）等还提出了基于中国市场的CH-3和CH-4因子模型。这些因子模型往往基于上市公司的财务指标，构建排序并得到投资组合，获得跑赢市场的因子收益率。而Frazzini et al.（2014）是根据beta构建的BAB因子，在美国市场和中国市场均取得了良好的收益。在上述复刻中，中国市场的结果和美国市场存在的差异也是值得后续探讨的部分。

Novy-Marx and Velikov（2022）在JFE上的文章Betting Against Betting Against Beta（BABAB）对Frazzini et al.（2014）的BAB提出了质疑。BABAB指出BAB使用的估计beta的方法，即通过不同的时间窗口分别计算波动率和相关系数，存在诸多问题。这会导致当市场处于高波动时，这种方法计算出来的beta比传统方法计算的beta更低；而当市场处于低波动时，这种方法计算出来的beta比传统方法计算的beta更高。此外，BAB因子构造时，权重采用的是按照排名z构造权重，BABAB指出这样构造的组合在小市值因子上有暴露。而小市值因子在美股长期有效，它对BAB的收益率产生了正贡献。

Frazzini et al.（2014）的文献固然贡献很大，他提出的BAB因子能够获得很高的收益率。他开创出的“分离式”计算beta的方法，也在后续被相关研究所使用。但是对于这样一篇在学术界也业界影响力都很大的文献，我们也应该从理性的角度看待它所使用的方法，所谓批判性阅读。而Novy-Marx and Velikov（2022）的BABAB就是这样做的，或许还能够提出BABABAB。而beta作为实证资产定价的一个绕不开的话题，从Black et al.（1972）的颠覆性研究开始，一直作为金融计量学者的研究重点，有历史的传承，也有新的颠覆和创新。这正是这门新兴学科的迷人之处。

参考文献

Andrea Frazzini, Lasse Heje Pedersen. Betting against beta[J]. Journal of Financial Economics,2014,111(1).
F. Black, M.C. Jensen, M. Scholes. The Capital Asset Pricing Model: Some Empirical Tests[J]. Social Science Electronic Publishing, 1972.
F. Black. Capital Market Equilibrium with Restricted Borrowing[J]. Journal of Business, 1972.
Robert Novy-Marx, Mihail Velikov. Betting against betting against beta[J]. Journal of Financial Economics,2022,143(1).
Jianan Liu, Robert F. Stambaugh,Yu Yuan. Size and value in China[J]. Journal of Financial Economics,2019,134(1).
Eugene F. Fama, Kenneth R. French. A five-factor asset pricing model[J]. Journal of Financial Economics,2015,116(1).
Fama Eugene F., French Kenneth R… Common risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics,1993,33(1).
Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

附录（SAS代码）

BAB因子复刻SAS代码