灰色预测模型

一、什么是灰色预测

灰色系统是指系统数据有一些是未知，有一些是已知。白色系统是全都已知，黑色系统是全都未知。而灰色预测就是对含有已知和未知信息的系统进行预测，寻找数据变动规律，生成有较强规矩性的序列，再建立相应的微分方程模型，来对事物发展进行预测。

二、灰色预测建模流程图

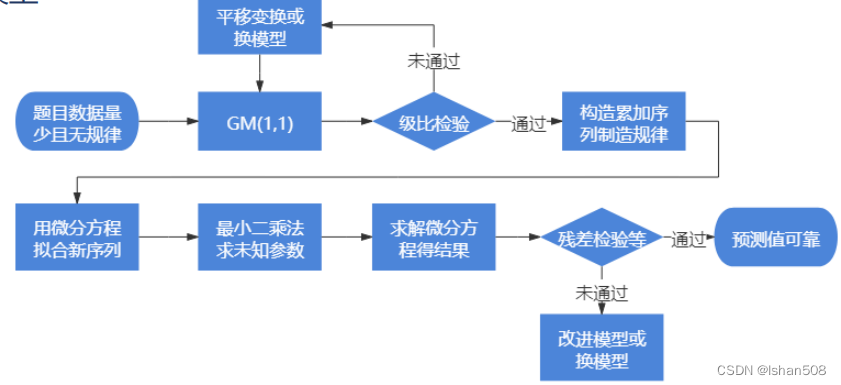
三、建模步骤

3.1、在建模最开始，需要进行数据的级比检验

为了确定数据使用GM(1,1)模型的可行性需要在一开始对原始数据进行级比检验：

3.2、训练求解模型

对原始序列X0累加求和得到新的序列X1，可用一个指数曲线乃至一条直线的表达式来逼近这个新序列，构建一阶常微分方程来求解拟合曲线的函数表达式 。表达式中含有未知数a和u，求出a和u即可解出预测方程。

对于a和u的求解我们采用最小二乘法：

参数a和u已求出，代入原微分方程，对微分方程进行求解。

3.3、模型检验

四、代码实现（python）

class GM11():
    def __init__(self):
        self.f = None  #预测方程
        
    def examine(self,X0):
        X1 = X0.cumsum() #对原始序列累加求和
        rho = [X0[i] / X1[i - 1] for i in range(1, len(X0))]
        rho_ratio = [rho[i + 1] / rho[i] for i in range(len(rho) - 1)]
        print("rho:", rho)
        print("rho_ratio:", rho_ratio)
        flag = True
        for i in range(2, len(rho) - 1):
            if rho[i] > 0.5 or rho[i + 1] / rho[i] >= 1:
                flag = False
        if rho[-1] > 0.5:
            flag = False
        if flag:
            print("数据通过光滑校验")
        else:
            print("该数据未通过光滑校验")

        '''判断是否通过级比检验'''
        lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]
        X_min = np.e ** (-2 / (len(X0) + 1))
        X_max = np.e ** (2 / (len(X0) + 1))
        for lambd in lambds:
            if lambd < X_min or lambd > X_max:
                print('该数据未通过级比检验')
                return
        print('该数据通过级比检验')
    def train(self,X0):
        
        X1 = X0.cumsum()
        Z = (np.array([-0.5 * (X1[k - 1] + X1[k]) for k in range(1, len(X1))])).reshape(len(X1) - 1, 1)
        A = (X0[1:]).reshape(len(Z), 1)
        B = np.hstack((Z, np.ones(len(Z)).reshape(len(Z), 1)))
        # 求常微分方程中的a u参数
        a, u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)
        u = Decimal(u[0])
        a = Decimal(a[0])
        #求解预测方程 
        self.f = lambda k: (Decimal(X0[0]) - u / a) * np.exp(-a * k) + u / a
    def predict(self, k):
        X1_hat = [float(self.f(k)) for k in range(k)]
        X0_hat = np.diff(X1_hat)  #还原原始序列
        X0_hat = np.hstack((X1_hat[0], X0_hat))  #添加上第一个数据
        return X0_hat  
    def evaluate(self, X0_hat, X0):
                S1 = np.std(X0, ddof=1)  # 原始数据样本标准差
        S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差
        C = S2 / S1  # 后验差比
        Pe = np.mean(X0 - X0_hat)
        temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1
        p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率
        print("原数据样本标准差：", S1)
        print("残差样本标准差：", S2)
        print("后验差比：", C)
        print("小误差概率p：", p)
import matplotlib.pyplot as plt
import numpy as np
#保证画图正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）

# 原始数据X
X = np.array(
    [21.2, 22.7, 24.36, 26.22, 28.18, 30.16, 32.34, 34.72, 37.3, 40.34, 44.08, 47.92, 51.96, 56.02, 60.14,
     64.58,
     68.92, 73.36, 78.98, 86.6])
# 训练集
X_train = X[:int(len(X) * 0.7)]
# 测试集
X_test = X[int(len(X) * 0.7):]

model = GM11()
model.isUsable(X_train)  # 判断模型可行性
model.train(X_train)  # 训练
Y_pred = model.predict(len(X))  # 预测
Y_train_pred = Y_pred[:len(X_train)]
Y_test_pred = Y_pred[len(X_train):]
score_test = model.evaluate(Y_test_pred, X_test)  # 评估

# 可视化
plt.grid()
plt.plot(np.arange(len(X_train)), X_train, '->')
plt.plot(np.arange(len(X_train)), Y_train_pred, '-o')
plt.legend(['负荷实际值', '灰色预测模型预测值'])
plt.title('训练集')
plt.show()

plt.grid()
plt.plot(np.arange(len(X_test)), X_test, '->')
plt.plot(np.arange(len(X_test)), Y_test_pred, '-o')
plt.legend(['负荷实际值', '灰色预测模型预测值'])
plt.title('测试集')
plt.show()