深入理解机器学习——过拟合（Overfitting）与欠拟合（Underfitting）

分类目录：《深入理解深度学习》总目录

机器学习的主要挑战是我们的算法必须能够在先前未观测的新输入上表现良好，而不只是在训练集上表现良好。在先前未观测到的输入上表现良好的能力被称为泛化（Generalization）。通常情况下，当我们训练机器学习模型时，我们可以使用某个训练集，在训练集上计算一些被称为 训练误差（Training Rrror）的度量误差，目标是降低训练误差。机器学习和优化不同的地方在于，我们也希望 泛化误差（Generalization Error）/测试误差（Test Rrror）很低。泛化误差被定义为新输入的误差期望。这里，期望的计算基于不同的可能输入，这些输入采自于系统在现实中遇到的分布。

通常，我们度量模型在训练集中分出来的测试集（Test Set）样本上的性能，来评估机器学习模型的泛化误差。如果训练集和测试集的数据是任意收集的，那么我们能够做的确实很有限。如果我们可以对训练集和测试集数据的收集方式有些假设，那么我们能够对算法做些改进。

训练集和测试集数据通过数据集上被称为数据生成过程（Data Generating Process）的概率分布生成。通常，我们会做一系列被统称为独立同分布假设的假设。该假设是说，每个数据集中的样本都是彼此相互独立的（Independent），并且训练集和测试集是同分布的（Identically Distributed），采样自相同的分布。这个假设使我们能够在单个样本的概率分布描述数据生成过程。然后相同的分布可以用来生成每一个训练样本和每一个测试样本。我们将这个共享的潜在分布称为数据生成分布（Data Generating Distribution），记作

      p 
     
    
      data 
     
    
   
  
    p_\text{data} 
   
  
pdata​。这个概率框架和独立同分布假设允许我们从数学上研究训练误差和测试误差之间的关系。

我们能观察到训练误差和测试误差之间的直接联系是，随机模型训练误差的期望和该模型测试误差的期望是一样的。假设我们有概率分布

     p 
    
   
     ( 
    
   
     x 
    
   
     , 
    
   
     y 
    
   
     ) 
    
   
  
    p(x, y) 
   
  
p(x,y)，从中重复采样生成训练集和测试集。对于某个固定的  
 
  
   
   
     w 
    
   
  
    w 
   
  
w，训练集误差的期望恰好和测试集误差的期望一样，这是因为这两个期望的计算都使用了相同的数据集生成过程。这两种情况的唯一区别是数据集的名字不同。

当然，当我们使用机器学习算法时，我们不会提前固定参数，然后采样得到两个数据集。我们采样得到训练集，然后挑选参数去降低训练集误差，然后采样得到测试集。在这个过程中，测试误差期望会大于或等于训练误差期望。以下是决定机器学习算法效果是否好的因素：

• 降低训练误差。
• 缩小训练误差和测试误差的差距。

这两个因素对应机器学习的两个主要挑战： 欠拟合（Underfitting）和 过拟合（Overfitting）。欠拟合是指模型不能在训练集上获得足够低的误差。而过拟合是指训练误差和和测试误差之间的差距太大。通过调整模型的容量（Capacity），我们可以控制模型是否偏向于过拟合或者欠拟合。通俗地，模型的容量是指其拟合各种函数的能力。容量低的模型可能很难拟合训练集。容量高的模型可能会过拟合，因为记住了不适用于测试集的训练集性质。

一种控制训练算法容量的方法是选择假设空间（Hypothesis Space），即学习算法可以选择为解决方案的函数集。例如，线性回归算法将关于其输入的所有线性函数作为假设空间。广义线性回归的假设空间包括多项式函数，而非仅有线性函数。这样做就增加了模型的容量。一次多项式提供了我们已经熟悉的线性回归模型，其预测如下：

       y 
      
     
       ^ 
      
     
    
      = 
     
    
      b 
     
    
      + 
     
    
      w 
     
    
      x 
     
    
   
     \hat{y} = b + wx 
    
   
 y^​=b+wx

通过引入

      x 
     
    
      2 
     
    
   
  
    x^2 
   
  
x2作为线性回归模型的另一个特征，我们能够学习关于 
 
  
   
   
     x 
    
   
  
    x 
   
  
x的二次函数模型：

  
   
    
     
     
       y 
      
     
       ^ 
      
     
    
      = 
     
    
      b 
     
    
      + 
     
     
     
       w 
      
     
       1 
      
     
    
      x 
     
    
      + 
     
     
     
       w 
      
     
       2 
      
     
     
     
       x 
      
     
       2 
      
     
    
   
     \hat{y} = b + w_1x + w_2x^2 
    
   
 y^​=b+w1​x+w2​x2

尽管该模型是输入的二次函数，但输出仍是参数的线性函数。因此我们仍然可以用正规方程得到模型的闭解。我们可以继续添加

     x 
    
   
  
    x 
   
  
x的更高幂作为额外特征。

当机器学习算法的容量适合于所执行任务的复杂度和所提供训练数据的数量时，算法效果通常会最佳。容量不足的模型不能解决复杂任务。容量高的模型能够解决复杂的任务，但是当其容量高于任务所需时，有可能会过拟合。

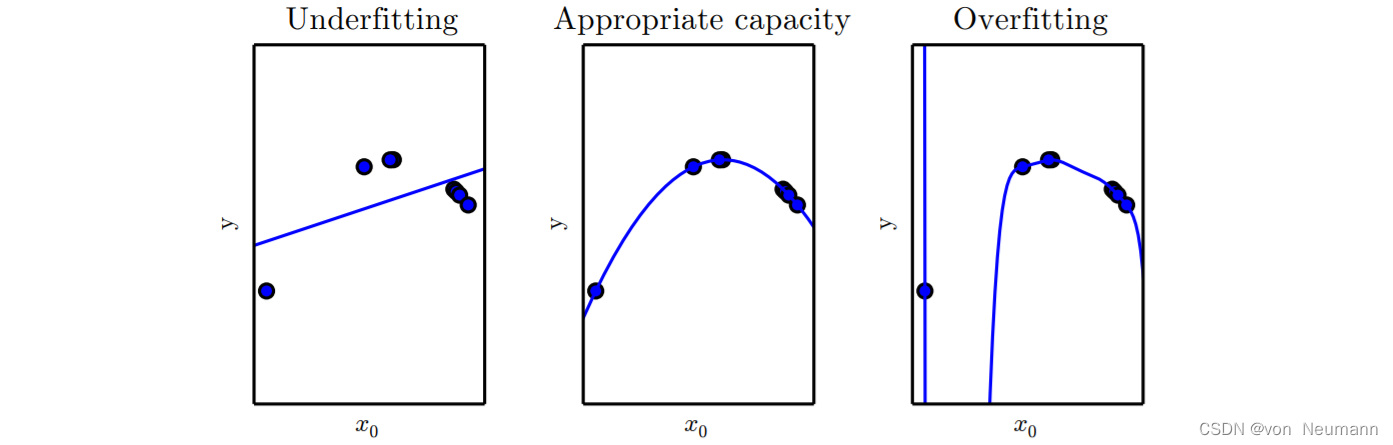
目前为止，我们探讨了通过改变输入特征的数目和加入这些特征对应的参数，改变模型的容量。事实上，还有很多方法可以改变模型的容量。容量不仅取决于模型的选择。模型规定了调整参数降低训练目标时，学习算法可以从哪些函数族中选择函数。这被称为模型的表示容量（Representational Capacity）。在很多情况下，从这些函数中挑选出最优函数是非常困难的优化问题。实际中，学习算法不会真的找到最优函数，而仅是找到一个可以大大降低训练误差的函数。额外的限制因素，比如
优化算法的不完美，意味着学习算法的有效容量（Effective Capacity）可能小于模型族的表示容量。

提高机器学习模型泛化的现代思想可以追溯到早在托勒密时期的哲学家的思想。许多早期的学者提出一个简约原则，现在广泛被称为 奥卡姆剃刀（Occam’s Razor）。该原则指出，在同样能够解释已知观测现象的假设中，我们应该挑选 ‘‘最简单’’ 的那一个。这个想法是在20世纪，由统计学习理论形式化并精确化的 。统计学习理论提供了量化模型容量的不同方法。在这些中，最有名的是 Vapnik Chervonenkis 维度（Vapnik-Chervonenkis dimension, VC）。VC维度量二元分类器的容量。VC维定义为该分类器能够分类的训练样本的最大数目。假设存在

     m 
    
   
  
    m 
   
  
m个不同 
 
  
   
   
     x 
    
   
  
    x 
   
  
x点的训练集，分类器可以任意地标记该 
 
  
   
   
     m 
    
   
  
    m 
   
  
m个不同的 
 
  
   
   
     x 
    
   
  
    x 
   
  
x点，VC维被定义为 
 
  
   
   
     m 
    
   
  
    m 
   
  
m的最大可能值。

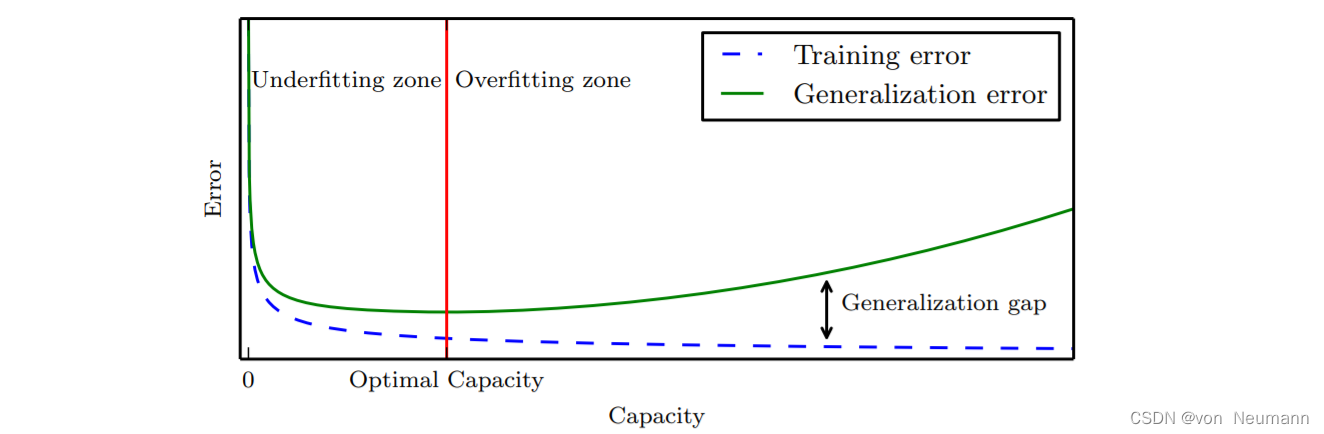
量化模型的容量使得统计学习理论可以进行量化预测。统计学习理论中最重要的结论阐述了训练误差和泛化误差之间差异的上界随着模型容量增长而增长，但随着训练样本增多而下降。这些边界为机器学习算法可以有效解决问题提供了理论验证，但是它们很少应用于实际中的深度学习算法。一部分原因是边界太松，另一部分原因是很难确定深度学习算法的容量。由于有效容量受限于优化算法的能力，确定深度学习模型容量的问题特别困难。而且对于深度学习中的一般非凸优化问题，我们只有很少的理论分析。

我们必须记住虽然更简单的函数更可能泛化（训练误差和测试误差的差距小），但我们仍然需要选择一个充分复杂的假设以达到低的训练误差。通常，当模型容量上升时，训练误差会下降，直到其渐近最小可能误差（假设误差度量有最小值）。通常，泛化误差是一个关于模型容量的U形曲线函数。为考虑容量任意高的极端情况，我们介绍非参数（Non-parametric）模型的概念。至此，我们只探讨过参数模型，例如线性回归。参数模型学习的函数在观测到新数据前，参数向量的分量个数是有限且固定的。非参数模型没有这些限制。

有时，非参数模型仅是一些不能实际实现的理论抽象（比如搜索所有可能概率分布的算法）。然而，我们也可以设计一些实用的非参数模型，使它们的复杂度和训练集大小有关。这种算法的一个示例是 k近邻（kNN，k-Nearest Neighbor）算法。

不像线性回归有固定长度的向量作为权重，最近邻回归模型存储了训练集中所有的

     X 
    
   
  
    X 
   
  
X和 
 
  
   
   
     y 
    
   
  
    y 
   
  
y。当需要为测试点 
 
  
   
   
     x 
    
   
  
    x 
   
  
x分类时，模型会查询训练集中离该点最近的点，并返回相关的回归目标。我们也可以将参数学习算法嵌入另一个增加参数数目的算法来创建非参数学习算法。例如，我们可以想象这样一个算法，外层循环调整多项式的次数，内层循环通过线性回归学习模型。理想模型假设我们能够预先知道生成数据的真实概率分布。然而这样的模型仍然会在很多问题上发生一些错误，因为分布中仍然会有一些噪声。在监督学习中，从 
 
  
   
   
     x 
    
   
  
    x 
   
  
x到 
 
  
   
   
     y 
    
   
  
    y 
   
  
y的映射可能内在是随机的，或者 
 
  
   
   
     y 
    
   
  
    y 
   
  
y可能是其他变量（包括 
 
  
   
   
     x 
    
   
  
    x 
   
  
x在内）的确定性函数。从预先知道的真实分布 
 
  
   
   
     p 
    
   
     ( 
    
   
     x 
    
   
     , 
    
   
     y 
    
   
     ) 
    
   
  
    p(x, y) 
   
  
p(x,y)预测而出现的误差被称为贝叶斯误（Bayes

Error）。

训练误差和泛化误差会随训练集的大小发生变化。泛化误差的期望从不会因训练样本数目的增加而增加。对于非参数模型而言，更多的数据会得到更好的泛化能力，直到达到最佳可能的泛化误差。任何模型容量小于最优容量的固定参数模型会渐近到大于贝叶斯误差的误差值。值得注意的是，具有最优容量的模型仍然有可能在训练误差和泛化误差之间存在很大的差距。在这种情况下，我们可以通过收集更多的训练样本来缩小差距。

没有免费午餐定理

学习理论表明机器学习算法能够在有限个训练集样本中很好地泛化。这似乎违背一些基本的逻辑原则。归纳推理，或是从一组有限的样本中推断一般的规则，在逻辑上不是很有效。为了逻辑地推断一个规则去描述集合中的元素，我们必须具有集合中每个元素的信息。在一定程度上，机器学习仅通过概率法则就可以避免这个问题，而无需使用纯逻辑推理整个确定性法则。机器学习保证找到一个在所关注的大多数样本上可能正确的规则。

可惜，即使这样也不能解决整个问题。机器学习的没有免费午餐定理（No Free Lunch Theorem）表明，在所有可能的数据生成分布上平均之后，每一个分类算法在未事先观测的点上都有相同的错误率。换言之，在某种意义上，没有一个机器学习算法总是比其他的要好。我们能够设想的最先进的算法和简单地将所有点归为同一类的简单算法有着相同的平均性能（在所有可能的任务上）。

幸运的是，这些结论仅在我们考虑所有可能的数据生成分布时才成立。在真实世界应用中，如果我们对遇到的概率分布进行假设的话，那么我们可以设计在这些分布上效果良好的学习算法。这意味着机器学习研究的目标不是找一个通用学习算法或是绝对最好的学习算法。反之，我们的目标是理解什么样的分布与人工智能获取经验的 ‘‘真实世界’’ 相关，什么样的学习算法在我们关注的数据生成分布上效果最好。

参考文献：
[1] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015