Word Embedding
前言
前面我们已经了解了CNN卷积神经网络,这一篇文章我们将了解Word Embedding等词汇编码
一、One-hot编码
1.为什么使用one-hot编码?
首先我们得知道传统的编码方式是怎么样的。传统的编码是通过统计类型出现次数的多少来进行编码的,也就是类别A出现的次数为m,类别B出现的次数为n,那么他们就分别编码为m,n。这样编码有可能导致求加权平均值的时候衍生成为其他类别,会体现不同类别的大小关系,误差较大。所以我们需要采用一种新的编码方式:one-hot编码(独热编码)
2.什么是one-hot编码?
使用N位状态寄存器来对N个状态进行编码,每个状态都有它独立的寄存器位,并且在任意时候,其中只有一位有效。
3.one-hot编码的优缺点
- 优点:
- 解决了分类器不好处理离散数据的问题。使用 one-hot 编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值 就 对应欧式空间的某个点。将离散型特征使用 one-hot 编码,确实会让特征之间的距离计算更加合理
- 在一定程度上也起到了 扩充特征 的作用。
- 缺点:
- 它是一个词袋模型,不考虑词与词之间的顺序。
- 它假设词与词相互独立,不能体现词汇间的相似性
- 每个单词的one-hot编码维度是整个词汇表的大小,维度非常巨大,编码稀疏,会使得计算代价变大。
二、Word Embedding(词嵌入)
1.什么是Word Embedding?
将word看作最小的一个单元,将文本空间中的某个word,通过一定的方法,映射或者说嵌入(embedding)到另一个数值向量空间。
Word Embedding的输入是原始文本中的一组不重叠的词汇,将他们放到一个字典里面,例如:[“cat”, “eat”, “apple”],就可以作为一个输入。
Word Embedding的输出就是每个word的向量表示,变成一个矩阵。
2.Word Embedding的优点:
- 对比one-hot高维稀疏向量,embedding维度低,连续向量,方便模型训练;
- 语意相似的词在向量空间上也会比较相近
- 一个向量可以编码一词多义(歧义需要另外处理);
- 天然有聚类后的效果,,是一种无监督学习。
- 罕见词也可以学到不错的表示。

3.基于计数的Word Embedding
1.基于计数的Word Embedding的优缺点
- 优点:
- 训练非常迅速
- 能够有效的利用统计信息。
- 缺点:
- 主要用于获取词汇之间的相似性(其他任务表现差)
- 给定大量数据集,重要性与权重不成比例。
2.Co-Occurence Vector(共现向量)
相似的单词趋向于有相似的上下文(context),我们可以构建一套算法,来实现基于上下文的特征构建。
当我们设置Context Window大小为2,范围为前后两个word,那么对于such这个词,他的Context Window就是下面绿色部分。
对于He is not lazy. He is intelligent. He is smart.
以He这这个单词举例,他在词料库里面的所有Context Window里面与is为之共现的词语的次数就是共现矩阵中is的次数
这个语料库来说,共现矩阵应该为: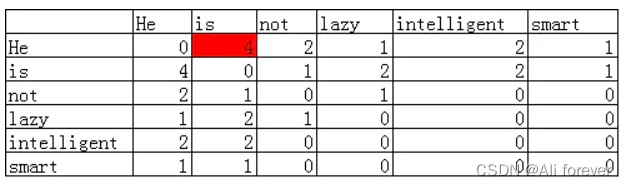
共现矩阵最大的优势是这种表示方法保留了语义信息,例如,通过这种表示,就可以知道哪些词语之间是相对较近的,哪些词语之间是相对较远的。
4.基于预测的Word Embedding
1.基于预测的Word Embedding的优缺点:
- 优点:
- 能够对其他任务有普遍的提高
- 能够捕捉到含词汇相似性外的复杂模式
- 缺点:
- 由于词和向量是一对一的关系,所以多义词的问题无法解决
- Word2vec 是一种静态的方式,虽然通用性强,但是无法针对特定任务做动态优化
- 没有充分利用所有的语料有存在浪费
2.CBOW(continues bag of words)
对于该语料而言,我们先对其做一个one-hot编码,然后选取Context Window为2,那么模型中的就产生了一对input和target
- 将产生的两个四维的vector输入到神经网络里面,连接激活函数。激活函数在输入层和隐藏层之间,每个input vector分别乘以一个VxN维度的矩阵,得到后的向量各个维度做平均,得到隐藏层的权重。隐藏层乘以一个NxV维度的矩阵,得到output layer的权重;
- 由于隐藏层的维度设置为理想中压缩后的词向量维度。示例中假设我们想把原始的4维的原始one-hot编码维度压缩到2维,那么N=2;
- 输出层是一个softmax层,用于组合输出概率。所谓的损失函数,就是这个output和target之间的的差(output的V维向量和input vector的one-hot编码向量的差),该神经网络的目的就是最小化这个loss;
- 优化结束后,隐藏层的N维向量就可以作为Word-Embedding的结果。
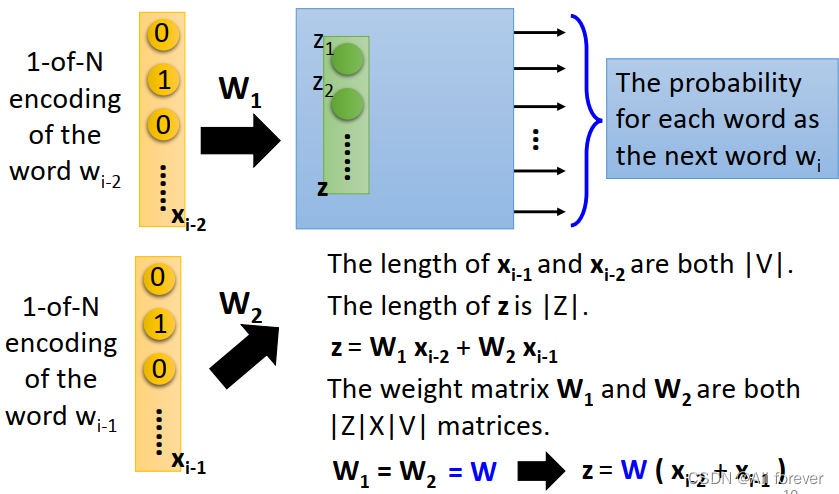
如此一来,便得到了既携带上下文信息,又经过压缩的稠密词向量。
3.Skip – Gram
这个方法可以看作是CBOW的翻转版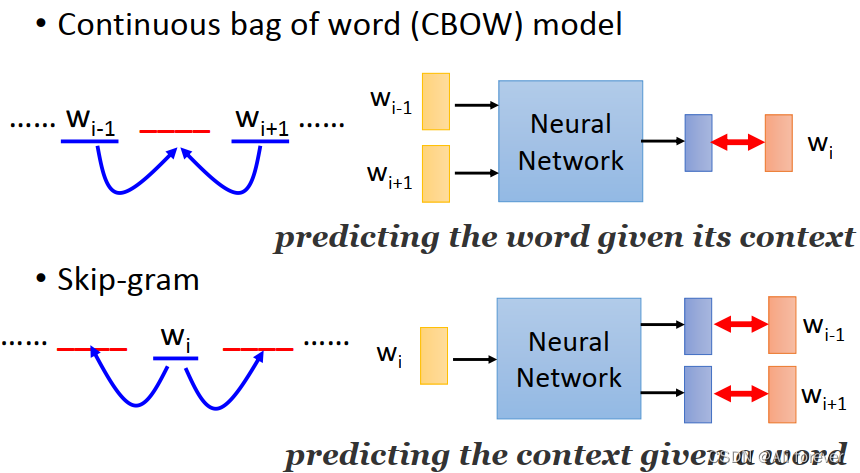
5.Glove(Global Vectors for Word Representation)
Glove算法是一种基于全局词频统计的回归算法。它不是基于神经网络的,而是基于最小二乘原理的回归方法。
它结合了上面两种算法的优点,可以有效的利用全局的统计信息。
它的过程如下:
- 根据语料库构建一个共现矩阵X,提出了一个衰减函数用于计算权重,也就是说距离越远的两个单词所占总计数的权重越小。
- 构建词向量(Word Vector)和共现矩阵(Co-ocurrence Matrix)之间的近似关系,论文的作者提出以下的公式可以近似地表达两者之间的关系: w i T w j ˜ + b i T + b j ˜ = log ( X i j ) w_i^T~{w_j}+b_i^T+~{b_j}=\log(X_{ij}) wiTwj˜+biT+bj˜=log(Xij) w i T w_i^T wiT和 w j ˜ ~{w_j} wj˜都是待求解的词向量, b i T b_i^T biT和 b j ˜ ~{b_j} bj˜都是偏置量
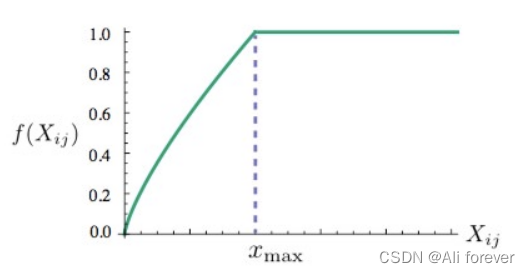
- 构造LossFunction。这个loss function的基本形式就是最简单的MSE,只不过在此基础上加了一个权重函数, J = ∑ i , j = 1 V f ( X i j ) ( w i T w j ˜ + b i T + b j ˜ − log ( X i j ) ) 2 J=\sum_{i,j=1}^Vf(X_{ij})(w_i^T~{w_j}+b_i^T+~{b_j}-\log(X_{ij}))^2 J=i,j=1∑Vf(Xij)(wiTwj˜+biT+bj˜−log(Xij))2
- 这些单词的权重要大于那些很少在一起出现的单词,所以这个函数要是非递减函数
- 但我们也不希望这个权重过大(overweighted),当到达一定程度之后应该不再增加;
- 如果两个单词没有在一起出现,他们应该不参与到loss function的计算当中去,所以 f ( 0 ) = 0 f(0)=0 f(0)=0
总结
本文介绍了Word Embedding,希望大家能从中获取到想要的东西,下面附上一张思维导图帮助记忆。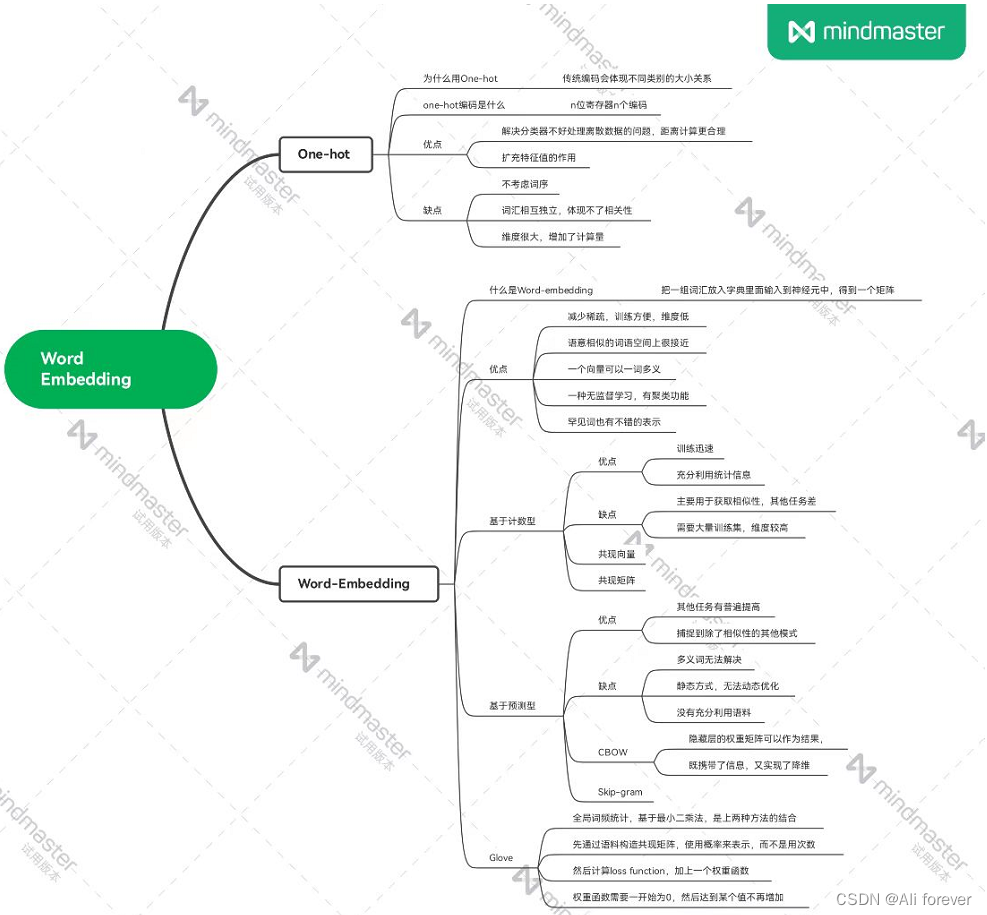
版权归原作者 Ali forever 所有, 如有侵权,请联系我们删除。