MFCC特征提取

     在语音识别方面，最常用到的语音特征就是梅尔倒谱系数（Mel-scaleFrequency Cepstral Coefficients，简称MFCC）。

    MFCC的提取过程包括预处理、快速傅里叶变换、Mei滤波器组、对数运算、离散余弦变换、动态特征提取等步骤。

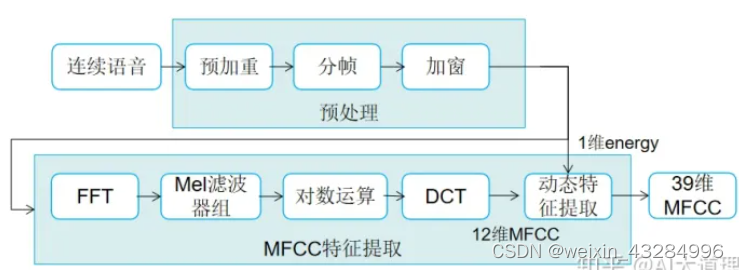
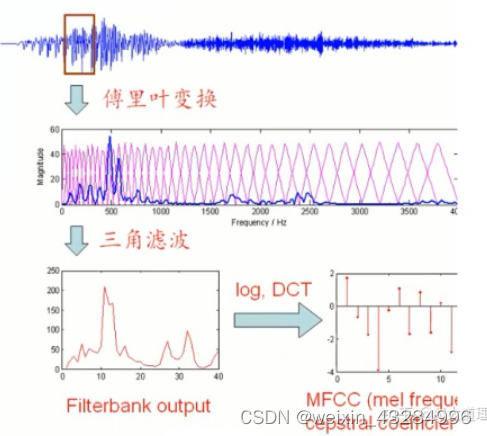
1.预处理

    对原始音频数据进行数字化、预滤波、预加重、端点检测、分帧、加窗等操作，使其信号特征更加明显，去除冗余数据。

2.快速傅里叶变换

    快速傅里叶变换即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。

    将音频从时域转换为频域。

3.Mel滤波器组

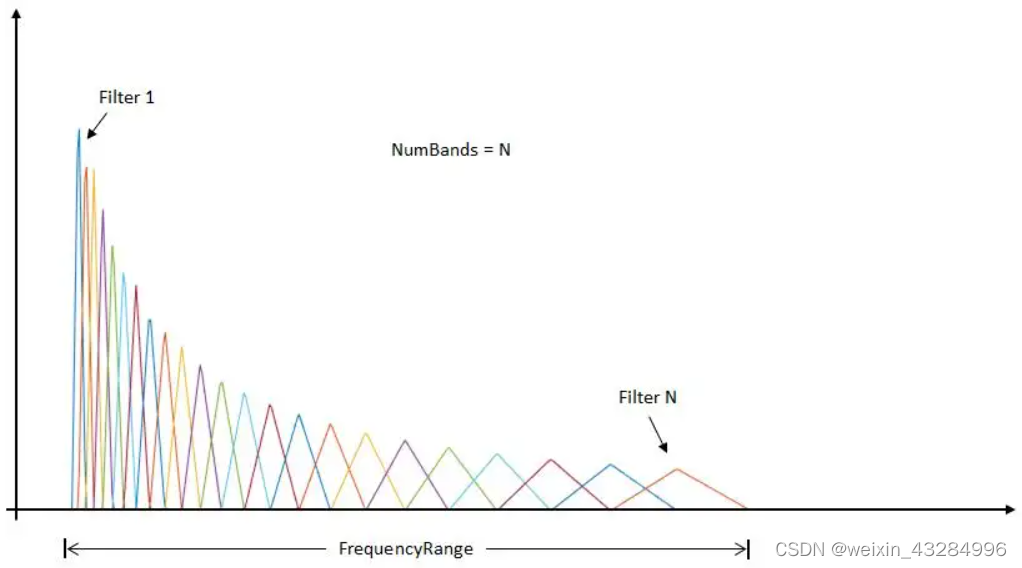
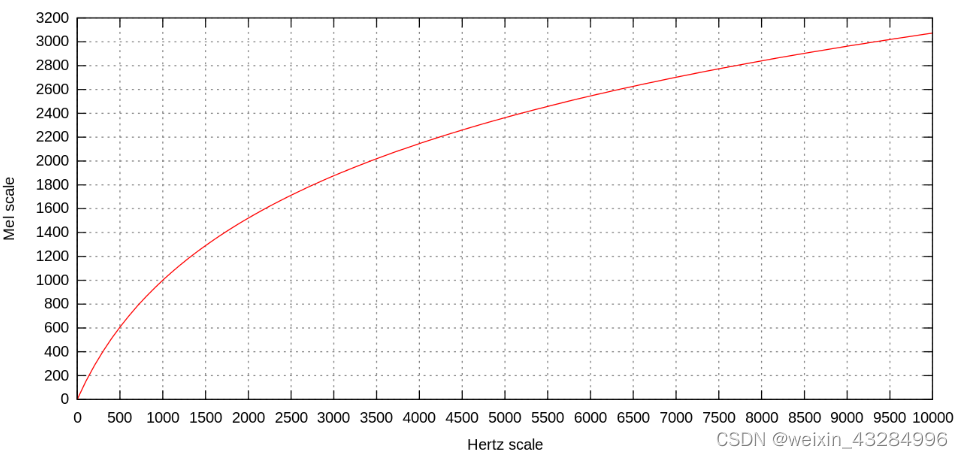
    研究表明，人类对频率的感知并不是线性的，并且对低频信号的感知要比高频信号敏感。对1kHz以下，与频率成线性关系，对1kHz以上，与频率成对数关系。频率越高，感知能力就越差。

    为了模拟人耳的听觉机制。从而研制出来了Mel滤波器组。

    所以，Ｍel滤波器组的在低频密集，高频稀疏。

梅尔刻度定义：

    它是Hz的非线性变换，对于以mel scale为单位的信号，可以做到人们对于相同频率差别的信号的感知能力几乎相同。

    HZ 与 mel scale 的相互转换关系如下：

    ![Mel\left ( f \right )=2595*log_{10}\left ( 1+\frac{f}{700} \right )](https://latex.codecogs.com/gif.latex?Mel%5Cleft%20%28%20f%20%5Cright%20%29%3D2595*log_%7B10%7D%5Cleft%20%28%201+%5Cfrac%7Bf%7D%7B700%7D%20%5Cright%20%29)

    ![f = Mel^{-1}\left ( f \right )=700\left ( 10^{\frac{m}{2595}}-1 \right )](https://latex.codecogs.com/gif.latex?f%20%3D%20Mel%5E%7B-1%7D%5Cleft%20%28%20f%20%5Cright%20%29%3D700%5Cleft%20%28%2010%5E%7B%5Cfrac%7Bm%7D%7B2595%7D%7D-1%20%5Cright%20%29)

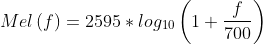
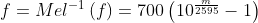
    如果对数以 e  为底，则系数的取值为 1125。

** 梅尔滤波器组的设计步骤：**

** **1）确定最低频率（0HZ）、最高频率（fs / 2）、Mel滤波器个数M（一般为24）

    2）在Mel频率下，这些滤波器的中心频率是等间距的，则：

    ![f_{d}\left ( mel \right ) = \frac{Mel\left ( f_{low} \right )+Mel\left ( f_{hig} \right )}{M+1}](https://latex.codecogs.com/gif.latex?f_%7Bd%7D%5Cleft%20%28%20mel%20%5Cright%20%29%20%3D%20%5Cfrac%7BMel%5Cleft%20%28%20f_%7Blow%7D%20%5Cright%20%29+Mel%5Cleft%20%28%20f_%7Bhig%7D%20%5Cright%20%29%7D%7BM+1%7D)

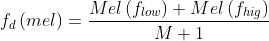
    3)每个滤波器的中心频率

            其中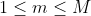： ![1\leq m\leq M](https://latex.codecogs.com/gif.latex?1%5Cleq%20m%5Cleq%20M)，N为DFT的频率长度，fs 为频率采样频率。

    4）每个滤波器的函数如下：

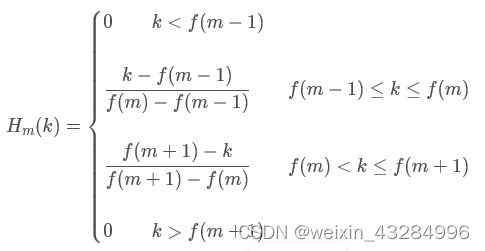
     综上4个步骤既可以生成如下等高梅尔滤波器：

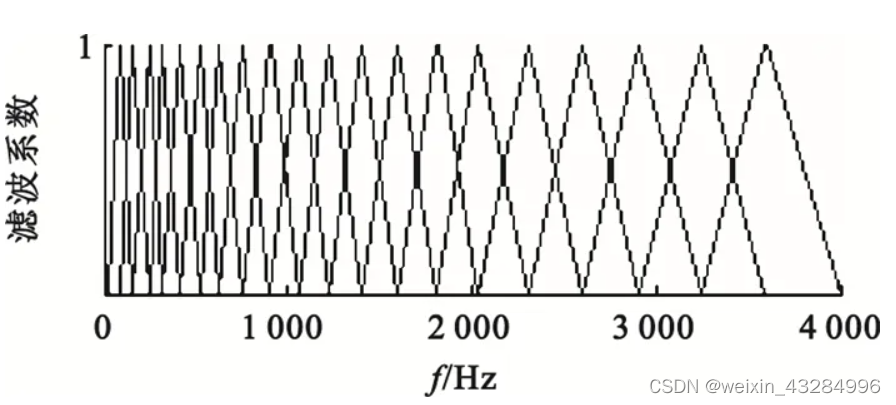
     这与开篇的梅尔滤波器略有不同，此处为各个滤波器等高，而开篇的滤波器不等高，这有什么影响吗？

    如开篇所示的不等高滤波器形式叫等面积梅尔滤波器。其在低频处密集高耸，高频处稀疏低矮。恰好对应了频率越高人耳越迟钝这一规律，在人声等领域有广泛应用。但是如果在非人声领域就会丢掉很多高频信息，此时常用等高梅尔滤波器。

    三角带通滤波器有两个主要目的：

    1）对频谱进行平滑化，并消除谐波的作用，突显原先语音的共振峰。频谱有包络和精细结构，分别对应音色与音高。对于语音识别来讲，音色是主要的有用信息，音高一般没有用。在每个三角形内积分，就可以消除精细结构，只保留音色的信息。

    2）傅里叶变换得到的序列很长（一般为几百到几千个点），把它变换成每个三角形下的能量，可以减少数据量。

生成Mel语谱图：

    能量谱，也称为能量谱密度。是指用密度的概念表示信号能量在各频率点的分布情况。也即是说，对能量谱在频域上积分就可以得到信号的能量。能量谱是信号幅度谱的模的平方，其量纲是焦/赫。

    （补充：能量信号和功率信号的分别 - 知乎）

    将能量谱通过一组Mel尺度的三角形滤波器组，其公式为：

    ![Y_{t}\left ( m \right )=\sum_{k=1}^{N}H_{m}\left ( k \right )\left | X_{t}\left ( k \right ) \right |^{2}](https://latex.codecogs.com/gif.latex?Y_%7Bt%7D%5Cleft%20%28%20m%20%5Cright%20%29%3D%5Csum_%7Bk%3D1%7D%5E%7BN%7DH_%7Bm%7D%5Cleft%20%28%20k%20%5Cright%20%29%5Cleft%20%7C%20X_%7Bt%7D%5Cleft%20%28%20k%20%5Cright%20%29%20%5Cright%20%7C%5E%7B2%7D)

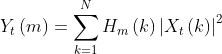
    得到梅尔语谱图：

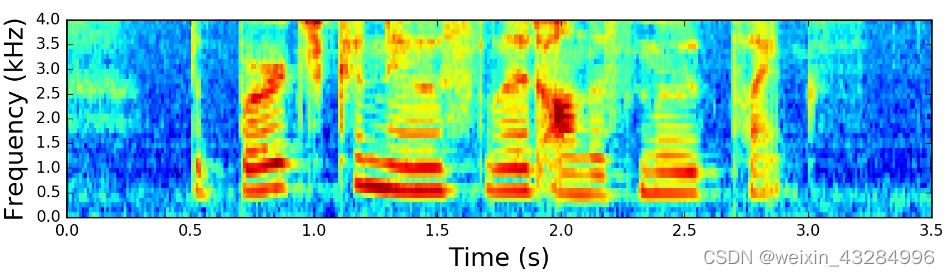
    其中横轴为时间，纵轴为频率，颜色深浅为能量。 

4.对数运算

    对数运算包括取模和log运算。

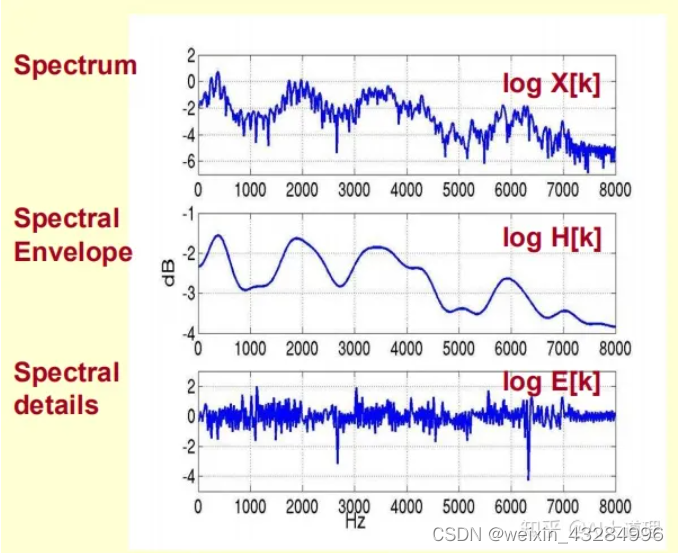
    将原始语音信号经过傅里叶变换得到频谱：

    ![X[k]=H[k]E[k]](https://latex.codecogs.com/gif.latex?X%5Bk%5D%3DH%5Bk%5DE%5Bk%5D)

    取模是仅使用幅度值，忽略相位的影响，因为相位信息在语音识别中作用不大。

    ![\left | X[k] \right |=\left | H[k] \right |\left | E[k] \right |](https://latex.codecogs.com/gif.latex?%5Cleft%20%7C%20X%5Bk%5D%20%5Cright%20%7C%3D%5Cleft%20%7C%20H%5Bk%5D%20%5Cright%20%7C%5Cleft%20%7C%20E%5Bk%5D%20%5Cright%20%7C)

    log 运算是为了分别包络和细节，包络代表音色，细节代表音高。显然语音识别是为了识别音色。另外，人的感知与频域的对数成成本，正好使用log运算对上述梅尔语谱图的纵轴进行对数缩放，可以放大低频率处的能量差异。

    ![log\left | X[k] \right |=log\left | H[k] \right |+log\left | E[k] \right |](https://latex.codecogs.com/gif.latex?log%5Cleft%20%7C%20X%5Bk%5D%20%5Cright%20%7C%3Dlog%5Cleft%20%7C%20H%5Bk%5D%20%5Cright%20%7C+log%5Cleft%20%7C%20E%5Bk%5D%20%5Cright%20%7C)

5.离散余弦变换（DCT）

    在上一步中，我们通过对数运算成功地把基音信息与声道信息变成了加性的。那么如何分离呢？它们有如下性质：  

频谱图中（注意是一帧原始语音信号FFT变换内）

    （1）基音信息在频域是快速变化的。

    （2）声道信息在频域是缓慢变化的。

倒谱的概念：

    定义：倒谱定义为信号短时振幅谱（功率谱）的对数傅里叶反变换

    特点：具有可近似地分离并能提取出频谱包络信息和细微结构信息的特点。

    可见我们只需要求出梅尔频谱的对数傅里叶反变换即可分离基音信息和声道信息。

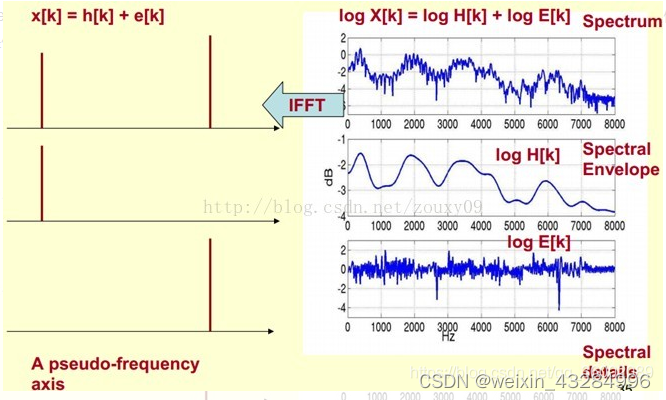
    ![x[k]=h[k]+e[k]](https://latex.codecogs.com/gif.latex?x%5Bk%5D%3Dh%5Bk%5D+e%5Bk%5D)

    在对数频谱上面做IFFT就相当于在一个伪频率（pseudo-frequency）坐标轴上面描述信号。所以虽然是时域序列，但它们所处的离散时域显然不同，此时称为倒谱频域。

    x[k]实际上就是倒谱Cepstrum。（这个是一个新造出来的词，把频谱的单词spectrum的前面四个字母顺序倒过来就是倒谱的单词了）。而我们所关心的h[k]就是倒谱的低频部分。h[k]描述了频谱的包络，它在语音识别中被广泛用于描述特征。

    在Mel频谱上面获得的倒谱系数h[k]就称为Mel频率倒谱系数，简称MFCC。

但是：MFCC特征使用的是DCT，而不是IDFT

** **由于许多要处理的信号都是实信号，在使用DFT时由于傅里叶变换时由于实信号傅立叶变换的共轭对称性导致DFT后在频域中有一半的负数部分，但这里复数系数并不太需要。DCT可以看作是IDFT的简化版，DCT得到的是实值系数。

    mel滤波器组有很多重叠部分，DCT可以在不同的mel频带上去相关性，因为在机器学习中，希望输入的特征之间的相关性越小越好。而且DCT相当于是对log mel谱的降维。

需要选择多少个系数 h[k]？

** **因为一般只关注声道信息，即谱包络成分（低频），因为声道信息包涵了我们感兴趣的成分，如音素信息、共振峰等，所有一般选前12-13个系数。

    由此得到的12维的MFCC特征如下： 

6.动态特征提取

    标准的倒谱参数MFCC只反映了语音参数的静态特性，语音的动态特性可以用这些静态特征的差分谱来描述。实验证明：把动、静态特征结合起来才能有效提高系统的识别性能。差分参数的计算可以采用下面的公式：

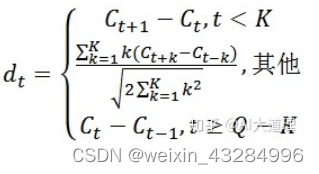
     其中，dt 表示第 t 个一阶差分，Ct 表示第 t 个倒谱系数，Q表示倒谱系数的阶数，K表示一阶导数的时间差，可取1或2。将上式的结果再代入就可以得到二阶差分的参数。

    因此，MFCC的全部组成其实是由： N维MFCC参数（N/3个MFCC系数+ N/3个一阶差分参数+ N/3个二阶差分参数）+帧能量（此项可根据需求替换）。这里的帧能量是指一帧的音量（即能量），也是语音的重要特征。

    最终得到36维MFCC图（3*12）：

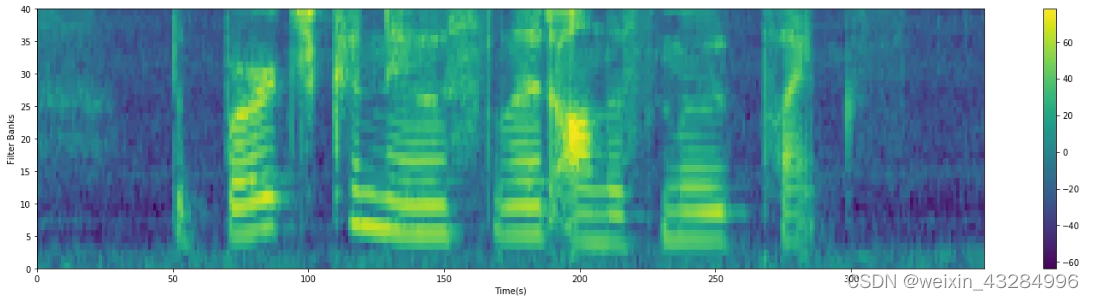
     （注：图为39（3*13）维MFCC图）