强化学习 | 策略梯度 | Natural PG | TRPO

学习情况：

🌱 耗时10天，学习了策略梯度。从基础概念开始，对Gradient、PG (REINFORCE、Q Actor-Critic、Advantage Actor-Critic)、Natural PG、TRPO、PPO 递进学习

🌱 近1个月的学习，发现RL跟我以前做DL (偏重对某个dataset调一个好的NN structure) 不太一样，很重视理论推导，且涉及多数学概念

🌱 查阅出现的数学概念，并根据论文推导每一步，这花了我很多时间。到后面发现这点很重要，尤其在从NPG到TRPO时

🌱 全文共1.3w字，含大量手写笔记。如有理解错误，欢迎指正

博客特色：

🌟 循序渐进，从 Gradient 至 Policy Gradient 至 Natural Policy Gradient 至 TRPO 至 PPO 递进式进习，夯实基础

🌟 从概览到细节，避免一叶障目。如写TRPO时，首先总结其在目标函数和梯度更新 (基于NPG) 两方面的改进，而后进行细节推导，最后将TRPO套入 "Trust Region Algorithm" 框架中深化理解

🌟 对涉及到的数学概念均撰写注释，包括导数、偏导、方向导数、梯度、概率分布、信息几何学、黎曼流形、KL divergence、熵、信息量、Fisher矩阵、Hessian矩阵、Jacobi矩阵、Lagrange Multiplier Method、Importance Sampling、MM算法、Conjugate Gradient、Trust Region等30余数学概念

🌟 大量手写笔记，逻辑清晰

🌟 前序文章：强化学习入门笔记 | UCL silver RL | UC Berkely cs285

目录：

Gradient

这一系列方法都是基于梯度的。简单复习下梯度概念，手写了下

Poliy Gradient

定义Policy Objective Function

首先，定义一下策略目标函数

求解Policy Gradient

那么对Policy Objective Function求一下Policy Gradient：

推导到上面红框里的公式后，发现对所有动作都使用同一个加权 (整条trajectory的reward)，这显然不合适。

如何对每个动作都采用不同的加权呢？

很自然地想到，可以使用从此动作之后的reward (即这个动作造成的后果有多好)，而非整条trajectory的reward(即所有动作累加起来的效果有多好)，这就是REINFORCE的思想了，如下

MC Policy Gradient (REINFORCE)

REINFORCE算法的伪代码如下：

Q Actor-Critic Policy Gradient

REINFORCE算法也有点问题，方差比较大，这是由于无偏估计问题：

简单比较一下使用MC采样的REINFORCE算法和使用TD采样的Q Actor-Critic算法，如下图：

Advantage Actor-Critic Policy Gradient

Q Actor-Critic可能存在这样一个问题：

当采样很少时，有的动作可能不会被取到。而这时其它被采样到的动作的Q都是正的。

这样的话，动作被Q加权后，被采样到的动作的概率在迭代中会升高，未被采样到的动作的概率在迭代中会降低（因为概率和为1）。

这并不有利于Exploration，况且未被采样到的动作的表现未必不好。

所以，我们需要 "负" 的奖励，即 "相对好"，直接的思路就是引入baseline作为 "好" 与 "不好" 的基准。

这就产生了Advantage Function (优势函数) 的概念， $\begin{equation} A(S, A, t)=Q(S, A)-V(S) \end{equation}$ ，这里的V(s)就是基准。

直观来理解一下，Q是在状态s下动作a的好坏，V是状态s的好坏 (其实V(s)是所有Q(s,a)的期望)。

那么如果Q>V，就是说当前动作能使当前状态更好，即相对是好的。如果Q<V，就是说当前动作使得当前状态更差，即相对是差的。

则使用A加权动作时，如果A>0，即这个动作是相对好的，则该动作的概率在迭代中会被提高；如果A<0，即这个动作是相对差的，则该动作的概率在迭代中会被降低。

在 $\begin{equation} A(S, A)=Q(S, A)-V(S) \end{equation}$ 中，一般将Q用V表示。表示V时，可以使用TD或MC采样方法，一般使用TD方法，TD(0)和n-step TD都可以。

在TD(0)中， $\begin{equation} Q(S, A)=R+\gamma V\left(S^{\prime}\right) \end{equation}$ ，则 $\begin{equation} A(S)=R+\gamma V\left(S^{\prime}\right)-V(S) \end{equation}$

其中，S'为S的后继状态

在n-step TD中， $\begin{equation} Q(S, A)=R_{t}+\gamma R_{t+1}+\ldots \gamma^{n-1} R_{t+n-1}+\gamma^{n} V\left(S^{\prime}\right) \end{equation}$ ，则 $\begin{equation} A(S)=R_{t}++\gamma R_{t+1}+\ldots \gamma^{n-1} R_{t+n-1}+\gamma^{n} V\left(S^{\prime}\right)-V(S) \end{equation}$

其中，S'为S的后继状态

则Advantage Actor-Critic算法的策略梯度表示为，

$\begin{equation} \nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} A^{n}\left(s_{t}^{n}, a_{t}^{n}\right) \nabla \log \pi_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right) \end{equation}$

常见Policy Gradient表达形式

那么最后总结一下策略梯度家族，一般策略梯度有以下几种表达形式：

用＂≈＂的原因是用采样代替期望，如果这里用期望表示直接用＂＝＂就行了

其实之前一直有点疑惑，到底▽J(θ)表示策略梯度，还是▽logΠ(a|s)是策略梯度。但是现在理解下，▽J(θ)其实就是▽logΠ(a|s)加了权重吧，重要的还是▽logΠ(a|s)表示出来的参数更新方向

一份总结得更全面的：

图取自 GAE论文中

Natural Policy Gradient

1998 - Armani - Why Natural Gradient?

1998 - Armani - Natural Gradient Works Efficiently in Learning

2002 - Kakade - A Natural Policy Gradient

常规梯度下降中，参数优化方向： $\begin{equation} \boldsymbol{\theta}_{k+1}=\boldsymbol{\theta}_{k}-\alpha_{k} \nabla J\left(\boldsymbol{\theta}_{k}\right) \end{equation}$

这个迭代公式的合理性依赖于一个底层事实：J(θ)的变化量和参数变化量在同一个Euclid空间中度量。

为什么这样说呢？因为▽J(θ)是θ的变化率，即变化量的速率

参数变化量固然在Euclid空间中度量，但是在很多问题中，J(θ)的变化量并不适合在欧氏空间中度量。例如当模型为 $\begin{equation} p(\boldsymbol{x} ; \boldsymbol{\theta}) \end{equation}$ ，即概率分布模型。

此时，分布函数 $\begin{equation} p(\boldsymbol{x} ; \boldsymbol{\theta}) \end{equation}$ 的数量变化 $\begin{equation} \Delta p(\boldsymbol{x} ; \boldsymbol{\theta}) \end{equation}$ 并不是概率属性变化的合理表征。

Π(a|s) 就是一种概率分布模型，所以求▽logΠ(a|s)时候，用欧氏空间中的"变化率"的概念，即使用欧式距离表征变化，来表示下降的方向不太合适，需要找一种概率属性变化更合理的表征方法

为什么说Π(a|s) 是一种概率分布模型？

它是stochastic policy，指state下可以采取不同action。它用条件概率表示，输出的是在该state下采取不同action的概率。经典的stochastic policy，如Vanilla/Nature PG，REINFORCE，Natural Actor-Critic.

为什么要输出概率呢？举一个例子，比如我 (agent) 站在宿舍门口(state)，Π判断我往前走的概率是0.7，向后/左/右走的概率各是0.1，那么policy会随机选择我接下来的action（概率大的被选到的可能性大）。这样agent就能自主移动啦。

所以如何衡量分布 $\begin{equation} p(\boldsymbol{x} ; \boldsymbol{\theta}) \end{equation}$ 和 $\begin{equation} p(\boldsymbol{x}, \boldsymbol{\theta}+\Delta \boldsymbol{\theta}) \end{equation}$ 的概率属性距离？

在信息几何中，可以将概率分布模型 $\begin{equation} p(\boldsymbol{x} ; \boldsymbol{\theta}) \end{equation}$ 全体视为参数空间中的一个黎曼流形，可以使用KL-divergence来衡量分布的概率属性距离，此时Fisher Information Matrix是黎曼流形的Riemann度量。

对这句话的几个名词（信息几何学、黎曼流形、KL-divergence、Fisher Information Matrix）解释一下：

信息几何学是一个用微分流形或者更进一步黎曼流形来研究概率分布的学科。主要的思想是以Fisher information作为黎曼度量建立一个黎曼流形，概率分布的parameter处在这个流形中，也就说可以把这个流形看成是概率密度函数所在的空间

流形 (Manifold) 可理解为受一定约束的某个 (一维或多维) 变量所有可能状态的集合，是弯曲的 N实数描述的点集合。从局部(即每个点的邻域)来看，流形和欧氏空间没有什么不同，即流形的局部具有欧式空间性质。但是从总体来看，流形可以是某种"弯曲"的空间，和"平直"的欧氏空间并不相同。

例如，球是流形的一个例子（借这个例子好好品一下局部看近似于平直的欧氏空间，全局看是弯曲的，这句话是什么意思），球面上的任意一条经线或维线是一个子流形。

其实从Manifold这个词，manifold = many fold，流形由很多个曲片面构成。球也可以看作很多个圆型组成的呀，所以从微分几何角度，流形是有重叠的chart的光滑过渡 (把流体的任何一个微小的局部看作是欧几里德空间，称为一个chart)。

在欧氏空间中，两点间的距离为， $\begin{equation} d s=\left(\sum_{i=1}^{N} d x_{i}^{2}\right)^{1 / 2} \end{equation}$ 。而在黎曼流形中，两点间的距离是"曲线"（显然要大于欧氏空间中的距离）被定义为 $\begin{equation} d s=\left(\sum_{i_{s}=1}^{N} g_{i j} d x_{i} d x_{j}\right)^{1 / 2} \end{equation}$ 。其中， $\begin{equation} g_{i j} \end{equation}$ 是一个沿流形表面逐点定义的对称正定矩阵，称为Riemann度量，用来描述对距离元的矫正。定义了Riemann度量的微分流形称为黎曼流形(Riemann Manifold)

关于流形，可以参考下这个，这个链接。这个概念我也查了好久，需要反复理解。

流形拓展：

流形还有一个很有意思的点，关于相对于欧氏空间的 "降维"，即降低表示的参数数量：

有一个点集合，每个点都用10个实数描述，很费笔墨，可以改变坐标轴，让每一个点只用9个实数描述吗？如果可以，就叫做降到9维。一个点集合，最低可以降到几维呢?

选一点，关注它附近的100个邻点，若这些点用9个实数当坐标就足以表示出这点较近，那点较远，我们就说这些点可以降到9维。远处再选1点，关注其邻点，再操作降维一次。如此多次后，原集合分解成多个子集合并且每一个都降维，我们就说原集合可以降到9维。

举个栗子，在欧式空间中，描述一个球， $\begin{equation} (x-a)^{2}+(-b)^{2}+(z-c)^{2}=r^{2} \end{equation}$ ，要这个复杂的方程式。在黎曼空间中，描述一个球，R=r就够了。是不是就简单多了？感觉流形可以简化一些复杂的数学问题吧。

再插一个有意思的点，黎曼空间中的Natural Gradient是跟坐标无关的。而欧氏空间中的Gradient是跟坐标系选取有关的，使用极坐标算出来的梯度和正交坐标系算出来的梯度并不相同。而这也导致了NN的gradient vanish问题，如果NN做Natural Gradient Descent就没有问题。

KL-divergence其实就是相对熵啊。交叉熵耳熟不？交叉熵就是相对熵推导出来的，不过是把常数项去掉了而已。

信息量 $\begin{equation} I\left(x_{0}\right)=-\log \left(p\left(x_{0}\right)\right) \end{equation}$ ，p(x_0)代表x_0发生的概率。信息量和确定性成反比。比如，说"现在在下雨"，确定性很高，信息量很小。但是如果我说"明天会下雨"，确定性低了，信息量大了，因为这时就要去查天气预报看看明天什么天气、综合多年经验判断下天气预报预测得准不准。

熵就是信息量的期望， $\begin{equation} H(X)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(p\left(x_{i}\right)\right) \end{equation}$

相对熵又被称为KL-divergence。"相对嘛"，它用于衡量两个概率分布的相对差异。 $\begin{equation} D_{K L}(p \| q)=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right) \end{equation}$ ，衡量q和p有多像。在ML中，一般p是真实的，q是近似值，衡量下q有多逼近p就是看模型拟合得好不好。

将相对熵展开下， $\begin{equation} \begin{aligned} D_{K L}(p \| q) &=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(p\left(x_{i}\right)\right)-\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right) \\ &=-H(p(x))+\left[-\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{0}\right)\right)\right] \end{aligned} \end{equation}$ ，去掉前面的常数项，后面那项就是交叉熵啦。

交叉熵 $\begin{equation} H(p, q)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right) \end{equation}$

Fisher Information Matrix (费雪信息矩阵)：用来衡量样本信息量多少。如果Fisher很大，说明观测数据携带模型参数估计的信息量很大，说明能将参数估计得更准确，它的意义解释。Fisher矩阵被定义为score function (log likelihood的导数)的方差，即 $\begin{equation} I(\theta)=E\left[S(X ; \theta)^{2}\right]-E[S(X ; \theta)]^{2}=\operatorname{Var}[S(X ; \theta)] \end{equation}$ ，也被定义为log likelihood的Hessian矩阵的期望的负值，即 $\begin{equation} E\left[S(\mathbf{X} ; \theta)^{2}\right]=-E\left(\frac{\partial^{2}}{\partial \theta^{2}} \log L(\mathbf{X} ; \theta)\right) \end{equation}$ ，具体数学意义看这个。Fisher scoring：将Hessian矩阵换成Fisher矩阵，因为有时候Fisher矩阵好求一些。即将 $\begin{equation} \theta_{t+1}=\theta_{t}-\eta_{t} H\left(\theta_{t}\right)^{-1} g\left(\theta_{t}\right) \end{equation}$ 换成 $\begin{equation} \theta_{t+1}=\theta_{t}-\eta_{t} I\left(\theta_{t}\right)^{-1} g\left(\theta_{t}\right) \end{equation}$

再科普下Hessian：

其实再查Hessian矩阵的时候，还顺带看了下Jacobi矩阵（但是跟本文没什么关系）：

概率分布是一种黎曼空间，KL散度是该分布空间的度量，而FIM定义了该分布空间的局部曲率

KL-div能够更好地衡量两个策略间的距离。使用KL-div对策略进行约束，能够使得两个策略之间不要相差太大。通过KL约束，解决了传统梯度算法中的"学习率"和"梯度方向"(策略空间上的) 的问题。

KL-div将对Natural Policy Gradient及底下要讲的TRPO和PPO的理解起到至关重要的作用。需要反复理解

在使用KL-div进行约束时，可以规定 $\begin{equation} D_{K L}(p(\boldsymbol{x}, \boldsymbol{\theta}) \| p(\boldsymbol{x}, \boldsymbol{\theta}+\Delta \boldsymbol{\theta}))=\epsilon(const) \end{equation}$ ，即规定两个策略的概率分布之间差异为ε(一个常数)，即进行等式约束。

当然，不等式约束也可以。不过是需要满足的KKT条件不同罢了。

使用Lagrange乘子法，将KL-div约束代入目标函数，则最大优化问题变成

$\begin{equation}\max _{\delta \boldsymbol{\theta}}\left\{(J(\boldsymbol{\theta}+\delta \boldsymbol{\theta})-J(\boldsymbol{\theta}))-\lambda\left(\|\delta \boldsymbol{\theta}\|_{\boldsymbol{G}}^{2}-\varepsilon^{2}\right)\right\} \end{equation}$

其中， $\begin{equation} \begin{aligned} &\|\delta \boldsymbol{\theta}\|_{\boldsymbol{G}} =D_{K L}(p(\boldsymbol{x}, \boldsymbol{\theta}) \| p(\boldsymbol{x}, \boldsymbol{\theta}+\delta \boldsymbol{\theta})) =\frac{1}{2} \delta \boldsymbol{\theta}^{\top} \boldsymbol{G}(\boldsymbol{\theta}) \delta \boldsymbol{\theta} \end{aligned} \end{equation}$

其中，G(θ)是Fisher Information Matrix，即 $\begin{equation} \boldsymbol{G} (\boldsymbol{\theta})=\int_{-\infty}^{+\infty} p(\boldsymbol{x}, \boldsymbol{\theta})\left(\frac{\partial}{\partial \boldsymbol{\theta}} \log p(\boldsymbol{x}, \boldsymbol{\theta})\right)\left(\frac{\partial}{\partial \boldsymbol{\theta}} \log p(\boldsymbol{x}, \boldsymbol{\theta})\right)^{\mathrm{T}} d \boldsymbol{x} \end{equation}$

拉格朗日乘子法是将约束条件带入到目标函数中，直接对目标函数求解就行了。

至于怎么推导的 $\begin{equation} \begin{aligned} D_{K L}(p(\boldsymbol{x}, \boldsymbol{\theta}) \| p(\boldsymbol{x}, \boldsymbol{\theta}+\delta \boldsymbol{\theta})) =\frac{1}{2} \delta \boldsymbol{\theta}^{\top} \boldsymbol{G} \boldsymbol{\theta} \delta \boldsymbol{\theta} \end{aligned} \end{equation}$ ，这里就懒得写了。详细可以看这个，就是对KL-div做了泰勒二阶近似其实。

关于拉格朗日乘子法科普：

那么继续。

将 $\begin{equation} \begin{aligned} &\|\delta \boldsymbol{\theta}\|_{\boldsymbol{G}} =D_{K L}(p(\boldsymbol{x}, \boldsymbol{\theta}) \| p(\boldsymbol{x}, \boldsymbol{\theta}+\delta \boldsymbol{\theta})) =\frac{1}{2} \delta \boldsymbol{\theta}^{\top} \boldsymbol{G}(\boldsymbol{\theta}) \delta \boldsymbol{\theta} \end{aligned} \end{equation}$ 代入， $\begin{equation}\max _{\delta \boldsymbol{\theta}}\left\{(J(\boldsymbol{\theta}+\delta \boldsymbol{\theta})-J(\boldsymbol{\theta}))-\lambda\left(\|\delta \boldsymbol{\theta}\|_{\boldsymbol{G}}^{2}-\varepsilon^{2}\right)\right\} \end{equation}$ 得到：

$\begin{equation} \max _{\delta \boldsymbol{\theta}}\left\{\nabla J(\boldsymbol{\theta})^{T} \delta \boldsymbol{\theta}-\frac{\lambda}{2} \delta \boldsymbol{\theta}^{T} \boldsymbol{G} \delta \boldsymbol{\theta}\right\} \end{equation}$

要求极值，求个导数吧 $\begin{equation} \frac{\partial}{\partial \delta \boldsymbol{\theta}}\left\{\nabla J(\boldsymbol{\theta})^{T} \delta \boldsymbol{\theta}-\frac{\lambda}{2} \delta \boldsymbol{\theta}^{T} \boldsymbol{G} \delta \boldsymbol{\theta}\right\}=\nabla J(\boldsymbol{\theta})-\lambda \boldsymbol{G} \delta \boldsymbol{\theta}=0 \end{equation}$

解出， $\begin{equation} \delta \boldsymbol{\theta}=\frac{1}{\lambda} \boldsymbol{G}^{-1} \nabla J(\boldsymbol{\theta}) \end{equation}$ 。

λ不重要，这个系数标量可以随便取。重要的是方向！

遂记参数的最佳变动方向为 $\begin{equation} \tilde{\nabla} J(\boldsymbol{\theta})=\boldsymbol{G}^{-1} \nabla J(\boldsymbol{\theta}) \end{equation}$ ，它就是自然梯度Natural Gradient啦

再回忆一下，Natural Gradient其实就是对策略加入了KL-div约束后算出来的梯度方向

则使用Natural Gradient的参数更新方程为：

$\begin{equation} \boldsymbol{\theta}_{k+1}=\boldsymbol{\theta}_{k}-\mu_{k} \nabla J\left(\boldsymbol{\theta}_{k}\right)=\boldsymbol{\theta}_{k}-\alpha_{k} \boldsymbol{G}^{-1}\left(\boldsymbol{\theta}_{k}\right) \nabla J\left(\boldsymbol{\theta}_{k}\right) \end{equation}$ ，

其中， $\begin{equation} \alpha=\sqrt{\frac{2 \varepsilon}{(\nabla J)^{\top} G(\nabla J)}} \end{equation}$ ，G(θ)是Fisher矩阵（部分文献中也喜欢用F或者I代表Fisher矩阵）

如果是梯度上升，这里就是加号了

关于α求解：

为什么在梯度的更新方程中保留了α这个学习率呢？不是KL-div已经用拉格朗日法转换进目标方程了吗？其实我也有疑惑。

我的理解是，参数θ的变化量是在欧氏空间中度量的，J(θ)的变化量是在黎曼空间中度量的。也就是parameter space和policy space并不是一个空间。学习率α是在parameter空间中的度量，而G^{-1}是policy space空间中的度量。而且这个α也是由KL-div计算出来的。或者是加一层"双重保险"嘛哈哈

或者从另外一个角度，Natural Gradient表征到欧氏空间中，其实归根到底还是一个"方向"，只不过这个方向比传统gradient表示得更好，更新时"方向"还是要乘以"步长"的

或者也可以理解成α是一个权重吧

Natural PG 是黎曼空间中真正得steepest ascent direction，它使用FIM替代单位矩阵，是一种策略间距离的更好的度量方式。

相较于传统PG的对超参α设置敏感、收敛曲线剧烈波动，NPG并不敏感于超参，且收敛曲线相对平缓。

以下TRPO在NPG的基础上，引入了IS表达目标函数，一次采样多次用于更新参数，提高了sample efficiency

TRPO

2015 - John Schulman - Trust Region Policy Optimization

TRPO核心概述

TRPO (Trust Region Policy Optimization)，即置信域策略优化。

TRPO分别在目标函数和梯度更新两方面做了改进

梯度更新方面的改进

TRPO基于Natural Policy Gradient (即用KL divergence约束policy，避免policy剧烈迭代)，做了以下两点改进：

第一点，为避免求解复杂的Fisher/Hessian逆运算，使用了conjugate gradient

第二点，将学习率换成 **α^j *** NPG原始的学习率，α∈(0,1)，由大至小线性搜索使目标函数大于0 (即本次迭代比上次好)，且符合KL divergence 的最小整数j值 (防止泰勒展开带来的误差)

即像原文讲的，"TRPO is related to prior methods(e.g.natural policy gradient) but make several changes,most notably by using a** fixed KL divergence** rather than a fixed penalty coeffificient"

目标函数方面的改进

在目标函数中引入Importance Sampling，提升了sample efficiency (原来每次采样完后只能更i性能一次梯度就把样本扔掉。引入IS后，可以多次使用θ'采样得的数据更新θ，即使用一批数据进行多次gradient ascent)。

还有一点有意思的是，作者将新的expeted disconted reward拆成了两部分，即旧的reward+某一部分。思想是，如果，理想情况下，"某一部分"恒为正，则reward是单调不减的，即每次策略都比之前的好。

这之外还有一点特殊的，在推导surrogate function的过程中，作者使用了MM算法，即找了目标函数的下界作为surrogate function

注意，一定要对前面的Natural Policy Gradient有透彻的了解才能看TRPO，否则会在某些细节处很迷惑。因为TRPO的论文中并没有对自然梯度有很多篇幅的介绍，所以要先有自然梯度的先验知识，才能研读TRPO

TRPO推导细节

那么对TRPO的行文细节理解一下

目标函数

先推导下目标函数

关于说TRPO单调不减这块我是有点疑惑的。看原文的时候，作者说的大概意思是如果使用deterministic policy的话，确实能保证单调不减，因为 $\begin{equation} \tilde{\pi}(s)=\arg \max _{a} A_{\pi}(s, a) \end{equation}$ ，只要有一个state-action对的Advantage Function大于0，就会选择它(当然如果大于0的多的话就选最大的)，因为determinstic policy是贪婪的。除非到了Advantage为0，即所有action都是一样好了，是收敛成功，停止了。作者又说，因为"unavoidable estimation and approximation error"，也可能出现 $\begin{equation} \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)<0 \end{equation}$ 的情况。感觉是因为噪声和建模不太准确吗？还是跟stochastic policy有关系？

总之，实际中，不一定能保证新策略的reward减旧策略的reward一定大于0，就是说不能保证一直单调递增。但是作者的确用了想单调收敛的思想来拆分目标函数。（可能是大概率会一直单调收敛，偶尔下降？还是有点疑惑）

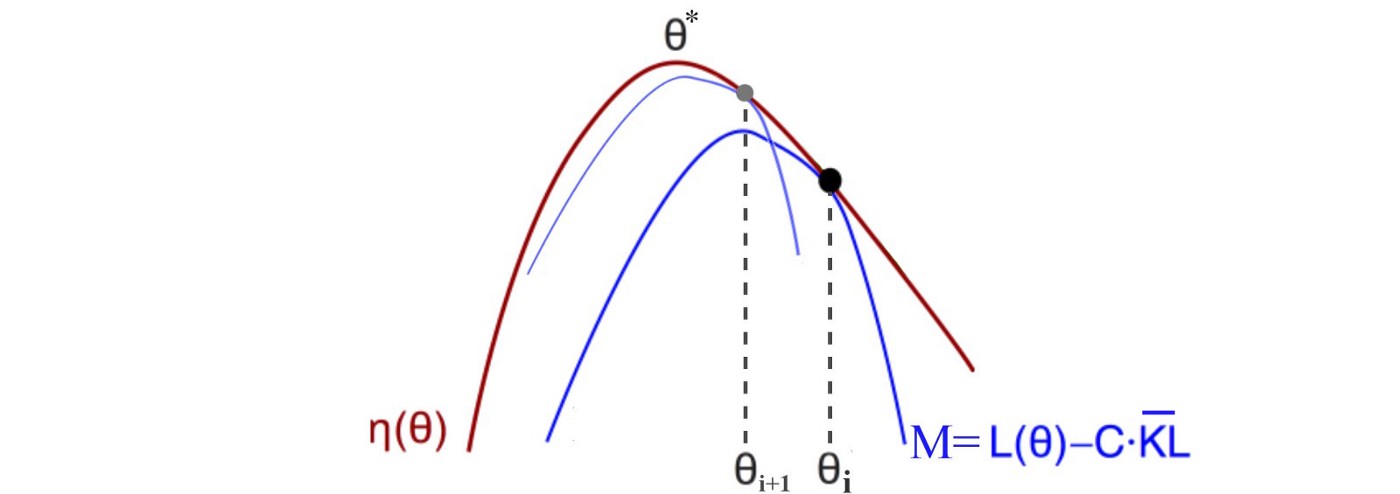
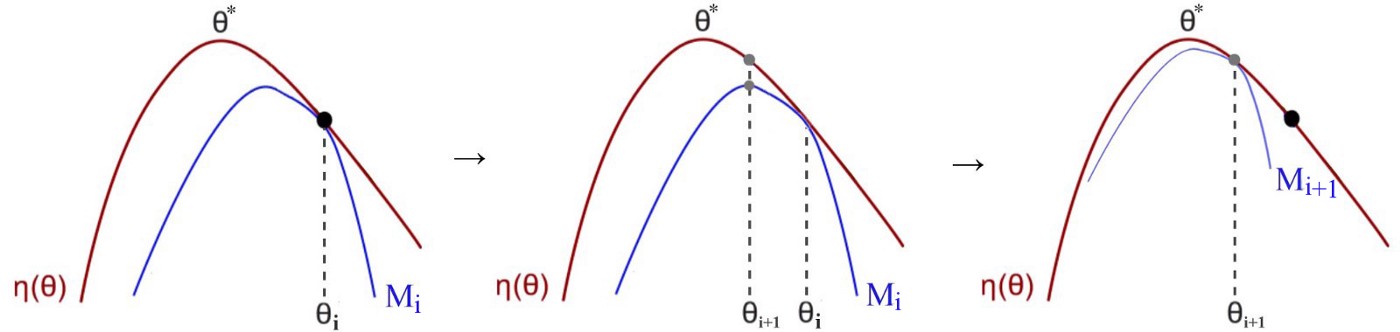
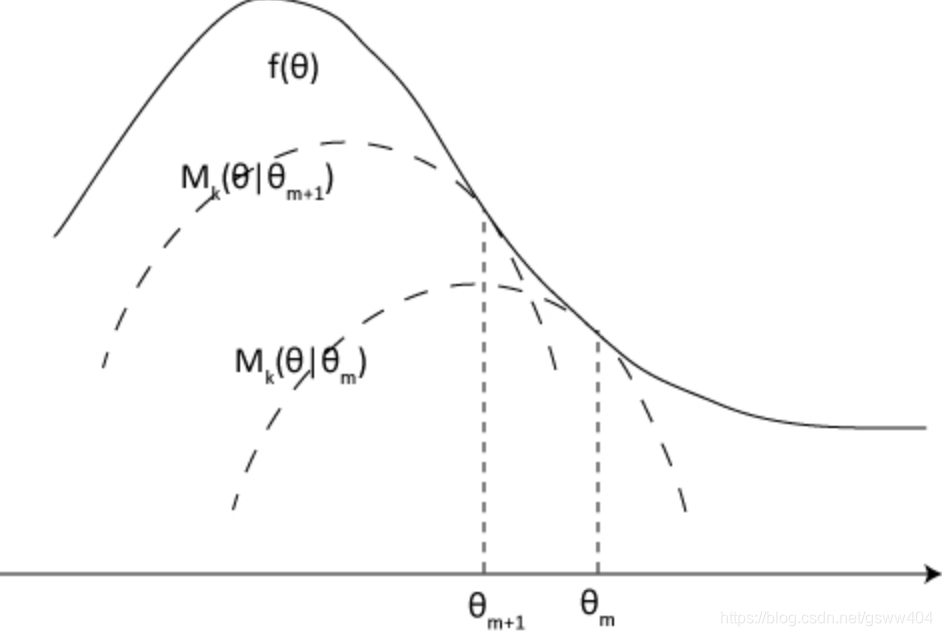
这其实就是trust region algorithm的图，取自这篇，讲得蛮好的这块

MM (Minorize-Maximization)

MM算法是一个迭代优化，其利用凸函数方法，以便找到他们的最大值或最小值,取决于所需的优化是最大化还是最小化。MM本身不是算法，而是描述如何构造优化算法。

Importance Sampling重要性采样：

好困，现在凌晨三点多了，不想打字了，看链接吧

ps：文章里还有一步，是说KL div的max太难求了，给sampling求平均了。这里不加进去了，只属于细节，不是关键点，怕打断推导思路

好了，目标函数推导出来了！下面就可以计算natural gradient，然后梯度上升了。跟上一part讲的梯度更新思路一样。

（但是好像看伪代码中，还是用的advantage value）

在实际应用中，会用样本平均值表示期望，论文中提到了两种采样方法：

关于vine sampling中的rollout，这篇解释得蛮清晰。且在vine sampling中，"trunk" 是回合更新的，而 "brank" 是单步更新的

"The vine method gives much better estimates of the advantage values. But the vine method must perform far more calls to the simulator for each these advantage estimates."

"The vine method requires us to generate multiple trajectories from each state in the rollout set ,which limits this algorithm to setting where the system can be reset to an arbitrary state. In contrast,the single path algorithm requires no state reset and can be directly implemented on a physical system."

梯度更新

接下来看下梯度的更新方程

首先按照Natural Policy Gradient的推导过程，我们得到以下更新方程：

$\begin{equation} \theta_{k+1}=\theta_{k}+\sqrt{\frac{2 \delta}{\hat{g}_{k}^{T} \hat{H}_{k}^{-1} \hat{g}_{k}}} \hat{H}_{k}^{-1} \hat{g}_{k} \end{equation}$

因为目标函数是求最大reward，所以做梯度上升哦

TRPO做了两点改进

其一，使用conjugate gradient (CG) 避免求解复杂的Hessian / Fisher矩阵逆运算

CG (共轭梯度法)：

如图，普通的梯度上升法并不是朝着全局最优解前进的，中间可能会出现梯度抵消的现象。如果目标函数是二次函数，我们可以使用共轭梯度法避免这种抵消。即搜索方向是正交的，最大搜索次数是参数的个数。

ps：CG的目标函数是二次型函数。但对于一般非线性函数，可以通过泰勒定理将其转为近似二次型

论文在附录C详细描述了CG，包括实验得出最佳迭代次数为10等。详细细节见论文

这篇讲得蛮清晰的

还有这篇综述《用共轭梯度法解决最优化问题》：

其二，TRPO将学习率换成 α^j * NPG原始的学习率，α∈(0,1)，j∈{0,1,2...}，由大至小线性搜索最小的j使得满足"improvement of the surrogate objective and satisfaction of the KL divergence constraint".

结合指数函数α^j的图像直观理解一下这句话的意思：

从大至小搜索使得目标函数提升且满足KL div的最小j，这时候α^j最大，其实就是在原来的NPG学习率前面乘了个(0,1)的系数，我们既希望满足条件又希望不要对NPG改变太大，所以找"最大"的最靠近1的系数，使NPG尽量不变。

论文在附录C描述了line search在其中的使用，细节见论文

"Starting with the maximal value of the step length β(即NPG算出来的原始学习率 $\begin{equation} \beta=\sqrt{\frac{2 \varepsilon}{(\nabla J)^{\top} G(\nabla J)}} \end{equation}$ )" in the previous paragraph,we shrink β exponentially (指数地，即α^j) until the objective improves.

"With this line search,the algorithm occasionally computes large steps that cause a catastrophic degradation of performance"

感觉line search是起到trust region的作用吧，通过这里可以再理解下TRPO将KL div放到约束项而非惩罚项的问题

贴下Natrual Gradient Algorithm和TRPO的伪代码对比下：

TRPO将KL div放在了约束项中，而非惩罚项，原因是δ好调，C不好调且太大。具体看这篇，这篇里也提到了这一点

看下TRPO更详细的伪代码：

Trust Region

好了，最后总结下Trust Region Policy Optimization中的 "Trust Region" 及 "Trust Region Algorithm" (数值优化领域的经典算法)

来看下什么是 "Trust Reigon"

看懂什么是Trust Region，再看下 Trust Region Algorithm是怎样的

它分为两步，"approximation" 和 "maximization"。

回想一下TRPO的整个流程，还真的是遵循这个大框架，即可以分为这两步，然后反复迭代：

PPO

2017 - John Schulman - Proximal Policy Optimization Algorithms

PPO核心概述

PPO同样是OpenAI的作品，它和TRPO是一个作者。PPO延续了TRPO的核心思想，即引入IS提高sample efficiency和约束两个策略间差异不要过大

但是相较TRPO，PPO简化了问题的求解方式，降低了计算复杂度，在实际工程中用得更多

在工程问题中，一般的直觉是，较小的问题用DQN作为baseline (收敛较快、便于训练)，较大、较复杂的问题用PPO作为baseline (效果较好)

PPO有许多version，在最初的论文中只介绍了两种，PPO1和PPO2

PPO1：TRPO之所以将KL div放到约束项而非惩罚项中，就是因为参数β难调。PPO1将KL div放到约束项中，自适应地动态调整KL前的参数，被称为 "Adaptive KL Penalty Coefficient"

PPO2：PPO2同样想使两个策略间差异不要过大，但是未使用KL约束，而是通过clip，巧妙设置新旧策略比值的范围

实验中，PPO2的效果强于PPO1

其实有NPG和TRPO的基础后，PPO就很好理解了。PPO与TRPO相同的部分将不再描述

PPO1：Adaptive KL Penalty Coefficient

"The theory justifying TRPO actually suggests using a penalty instead of a constraint".但因为权重β难以调整的问题，TRPO没有选择将KL div作为惩罚项放到目标函数进而解决无约束问题，而是将KL div作为hard constraint处理

而PPO1将KL div放到约束项中：

那么KL div前面的权重如何设置呢？

"Experiments show that it is not sufficient to simply choose a fixed penalty cofficient β and optimize the penalized objective with SGD.Additional modifications are required”.简单地设定一个权重值β在实验中表现不佳

所以PPO1中使用了自适应调整权重β的方法

步骤

即首先设置一个可接受的KL div最大值 $\begin{equation} \mathrm{KL}_{\max } \end{equation}$ 和可接受的KL div最小值 $\begin{equation} \mathrm{KL}_{\min } \end{equation}$

如果一轮优化完后，KL div太大，则说明后面的惩罚项 $\begin{equation} \beta \mathrm{KL}\left(\theta, \theta^{k}\right) \end{equation}$ 没有发挥作用，则增大β

如果一轮优化完后，KL div太小，则说明后面的惩罚项 $\begin{equation} \beta \mathrm{KL}\left(\theta, \theta^{k}\right) \end{equation}$ 的效果太强了，担忧只优化了后一项，这不是我们想要的，则减小β

即 $\begin{equation} \mathrm{KL}\left(\theta, \theta^{k}\right)>\mathrm{KL}_{\max } \end{equation}$ 时，减小β； $\begin{equation} \mathrm{KL}\left(\theta, \theta^{k}\right)<\mathrm{KL}_{\min } \end{equation}$ 时，增大β

伪代码

PPO2：Clipped Surrogate Objective

首先定义了新旧策略间的比值r(θ)，将L写成 $\begin{equation} L^{C P I} \end{equation}$

步骤

PPO2的main objective为：

min函数：在两个式子间取最小值

clip函数：

假设ε=2，则clip函数为， $\begin{equation} \operatorname{clip}\left(r_{t}(\theta), 0.8,1.2\right) \end{equation}$

即当 $\begin{equation} r_{t}(\theta) \end{equation}$ <0.8，则输出0.8；当 $\begin{equation} r_{t}(\theta) \end{equation}$ >1.2，则输出1.2；当 $\begin{equation} r_{t}(\theta) \end{equation}$ ∈[0.8,1.2]，则不裁剪，照旧输出 $\begin{equation} r_{t}(\theta) \end{equation}$

这样就保证了新旧策略的比值在区间 [0.8,1.2] 内，即两个策略不至于相差太大

PPO采用一阶优化加限制的形式，替代TRPO中的二阶优化，使用CLIP代替复杂的KL div计算，同样使得两个策略间差异不太大

PPO2设计得很巧妙的还有一点，就是在clip函数后乘了 $\begin{equation} {A}_{t} \end{equation}$

$\begin{equation} {A}_{t} \end{equation}$ 是有正负的啊。当这个动作 "相对好" 的时候， $\begin{equation} {A}_{t} \end{equation}$ >0；当这个动作 "相对差" 的时候， $\begin{equation} {A}_{t} \end{equation}$ <0

那么再搭配上min这个函数，就会有这样较有意思的效果：

实在太困了，我就自己懒得画了，别的博客中有张图，对min、A的正负对 $\begin{equation} L^{C P I} \end{equation}$ 的计算挺清晰的，但是跟上面这张论文里的图配色不太一样，A<0时候坐标轴也没倒过来。注意别看混了：

其中， $\begin{equation} r_{t}(\theta) \end{equation}$ 是绿色的线， $\begin{equation} \operatorname{clip}\left(r_{t}(\theta), 1-\epsilon, 1+\epsilon\right) \end{equation}$ 是蓝色的线。红色的线min取哪部分取决于A的正负

直观理解下，当A>0，即该state-action是相对好的，则希望增大这个state-action的概率，但是又不能增得太大导致 $\begin{equation} \frac{p_{\theta}\left(a_{t} \mid s_{t}\right)}{p_{\theta}\left(a_{t} \mid s_{t}\right)} \end{equation}$ 太大，即前后策略相差太大，故限制其比例不得大于1+ε

当A<0，即该state-action是相对差的，则希望减小这个state-action得概率，但是又不能减小太多使得 $\begin{equation} \frac{p_{\theta}\left(a_{t} \mid s_{t}\right)}{p_{\theta}\left(a_{t} \mid s_{t}\right)} \end{equation}$ 太小，即前后策略相差太大，故限制其比例不得小于1-ε

结合一些其它考虑，PPO2最后的objective：

$\begin{equation} L_{t}^{V F}(\theta) \end{equation}$ 是quared-error，表示为 $\begin{equation} \left(V_{\theta}\left(s_{t}\right)-V_{t}^{\operatorname{targ}}\right)^{2} \end{equation}$ ，S是entropy bonus

关于entropy bonus：

"If using a neural network architecture that shares parameters between the policy and value function, we must use a loss function that combines the policy surrogate and a value function error term. This objective can further be augmented by adding an entropy bonus to ensure sufficient exploration, as suggested in past work [Wil92; Mni+16]"

其中，估计advantage value用到了GAE (Generalized Advantage Estimator)：

了解GAE可以看下这篇和这篇

伪代码

PPO算法的大致流程，只需要在VPG基础上做较小的改动，即将目标函数换掉，并在每次更新时对该objective多次梯度上升即可

在这里插入图片描述

AC训练过程：

每轮迭代中，并行开N个Actor (θ') 与环境交互，采样N条长度为T的trajectory，即共收集NT个样本

使用GAE估计advantage value，和action probability一起存入buffer

从buffer中采样M (Minibatch Size)个样本，训练K个epoch (K其实是一个样本复用次数)

OpenAI baseline中的一般设置是，K = 3，Minibatch Size = NT / 4，则一轮迭代中，通过 SGD，参数更新12次

标签：人工智能强化学习增强学习

本文转载自: https://blog.csdn.net/qq_45832958/article/details/123357739
版权归原作者 111辄 所有，如有侵权，请联系我们删除。

强化学习 | 策略梯度 | Natural PG | TRPO | PPO