文章目录
自动驾驶系统由环境感知、规划、决策、控制等几个模块组成，其中环境感知需要用到诸如摄像头、毫米波雷达、激光雷达等传感设备来获取周围环境的信息。不同种的传感器有着不同的优势与缺陷，为了使感知层获得的信息更为丰富、准确，通常需要将不同的传感器进行融合。本文着重介绍多传感器融合的概念与相关知识，不具体介绍技术细节。
1. 运动感知类与环境感知类传感器
自动驾驶中的传感器一般分为运动感知类传感器与环境感知类传感器。
运动感知类传感器主要用以解决自动驾驶中的定位与建图问题。常见的传感器有全球定位系统（GNSS，Global Navigation Satellite System）、RTK（Real-Time Kinematic）、惯性传感器IMU(IMU,Inertial Measurement Unit)、轮速计（Wheel Speedometer）、激光雷达（LiDAR，Light Detection and Ranging）、相机（Camera）。
环境感知类传感器在自动驾驶中一般用于感知目标。常见的传感器有激光雷达（LiDAR，Light Detection and Ranging）、相机（Camera）、毫米波雷达（RaDAR，Radio Detection and Ranging，或者millimeter wave radar）、超声波雷达（ultrasonic radar）。
从传感器的功能角度看，上述两个方面的传感问题都需要用到多传感器融合。
下面是对常见传感器的总结。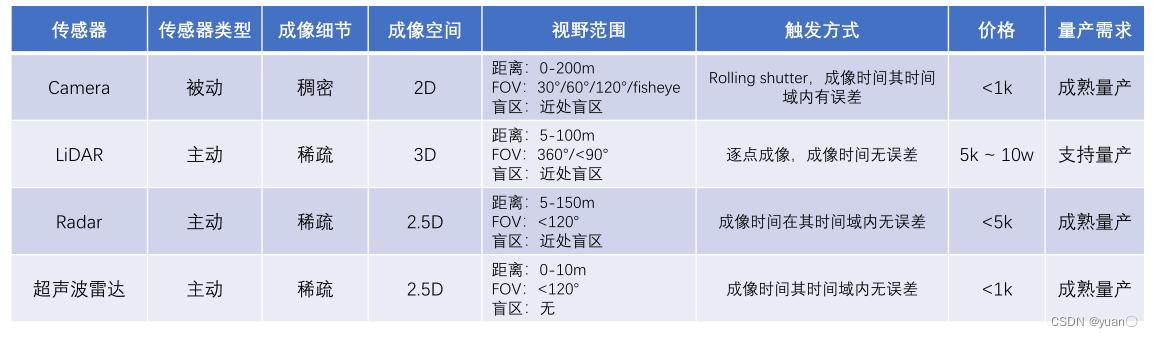
下面总结了传感器如何相互配合
- 多种电磁波与机械波配合
- 被动传感器与主动传感器配合
- 稀疏传感器与密集传感器搭配，2D与3D配合远中近距离均适合
- FOV可灵活搭配，可有效区分重点区域
- 时间戳误差可控，感知的维度各有所长
- 均已量产，LiDAR虽 成本高使用受限，但发展快
2. 为什么需要这么多传感器？
2.1 从需求侧分析
自动驾驶系统需要考虑多方面的因素：天气、光照条件、距离、维度及精度与系统级要求。除此之外，对于传感器，成本可控、满足车规要求也是十分重要的。
天气光照条件距离维度及精度系统级要求晴天白天盲区(0-2m)六自由度观测无漏检雨天黄昏近距离(2-40m)速度/加速度/角速度等无误检雾天黑夜中距离(40-80m)时间误差<10ms阴天阳光直射远距离(80-200m)位置误差<30cm雪天背光超远距离(200+m)
2.2 从供给侧分析
各种传感器各有优劣，一种传感器无法适配所有场景，因此需要出色的传感器融合技术。比如，摄像头颜色细节丰富、纹理细节丰富，但缺乏深度信息，且易受光照的影响；LiDAR具有完整的3D信息，对距离感知能力强，但成本高，量产难度大，对雨水、灰尘敏感；RaDAR全天候工作，速度感知能力强，量产成熟，但高度和角度精度低，静止障碍物感知能力弱。
3. 多传感器硬件系统的设计思路
对于自动驾驶汽车的多传感器硬件系统，一般从以下四个角度去考虑：感知区域、感知范围、优先级、冗余要求。
如图所示，对于自动驾驶汽车，将其行驶场景进行划分为5个区域。
区域0:常为车身感知盲区，主要用于慢速行驶的安全冗余以及泊车场景，优先级高;
区域1:主要用于前向行驶需求，通常分为三阶段，优先级高:
- 0-80m:要求感知精度高，高冗余
- 80-120m:要求感知精度中高，中等冗余
- 120-200m+:要求感知精度中等，冗余要求低
区域2/3:主要用于左右变道或转向场景，冗余要求较低，优先级中;
区域4:用于常规行驶的后向视野，冗余要求低，优先级中。
感知区域感知范围优先级冗余要求区域00-10m高高区域10-200m高高区域2/30-80m中中区域40-80m中中
4. 多传感器系统的时序闭环
4.1 传感器时钟闭环构建
用下面的例子介绍什么是时间闭环？
身在硅谷的A同学和身在北京的B同学约了北京时间明早9点，开一个简短的会。
北京时间早上九点是时序。同学与手机之间存在闭环，同学通过闹钟等方式查询时间是否到了北京时间早上九点；手机与网络存在闭环，通过同步时间完成闭环；最后通过协作分工达到运行流畅（大的闭环）。
如此可以得知时序闭环的目的——让所有的参与者都在同一个时序上运转并持续维护时序的高精度运行。
在现实物理世界中，通过时区的方式来达到时序闭环。
• 全球分时区，每个时区内独立计时
• 各时区与原子时钟同步，确保精度
那么自动驾驶中的传感器如何工作在同一时钟之下，达到时序闭环？
问题描述：
每种电子设备都有各自的时钟，起始时间均不相同，而且因晶振质量的差异，频率也不同。
同步误差分析：
传感器之间的时钟偏差，会导致各传感器检测到的障碍物位置发生偏差，自车速度越大，偏差越大。当车辆以120km/h的速度行驶时，若时钟偏差达到0.1s,则可以算出距离偏差达到了3.33m，偏差较大。
需求分析：
自动驾驶完整系统的误差需要控制在0.3m以内，通常需要将闭环时钟同步误差控制在微秒级别。
接着，需要将传感器接入已有的时钟同步闭环系统之中。如上图所示，有两种接口：一种通过车载计算平台与网络连接；另一种通过GNSS/IMU。
上图中，车辆通过车载计算平台与网络连接，与原子钟更新校正时间；通过GNSS/IMU校正时间。原子钟与GPS的时间都是精确的。
通过计算客户端client与服务端server之间的偏差offset，以1s为周期，根据offset调整client时钟，可将时钟误差稳定控制在微秒级别。
因此得出车载系统可以接入已有时钟同步闭环，精度满足需求。
再分析各传感器能否接入已有时钟同步闭环。
对于LiDAR,LiDAR设备支持两种时钟同步方式:
- IEEE 1588-2008(PTPv2):以太网接口同步;
- PPS脉冲信号+NMEA消息(GPS).
通过以上两种方式接入GNSS+IMU设备或者主机所属的以太网即可。以上同步周期进行，可控制在微秒级精度。
对于camera，非定制相机模组不支持时钟同步，定制相机可选择支持。对于radar，非定制Radar不支持时钟同步。对于超声波雷达非定制超声波雷达不支持时钟同步。
因此，在目前的多传感器系统中，时钟无法做到微秒级同步。
4.2 成像同步机制
在目前的多传感器系统中，时钟无法做到微秒级同步。因此，需要考虑在硬件层面上的同步——成像同步。
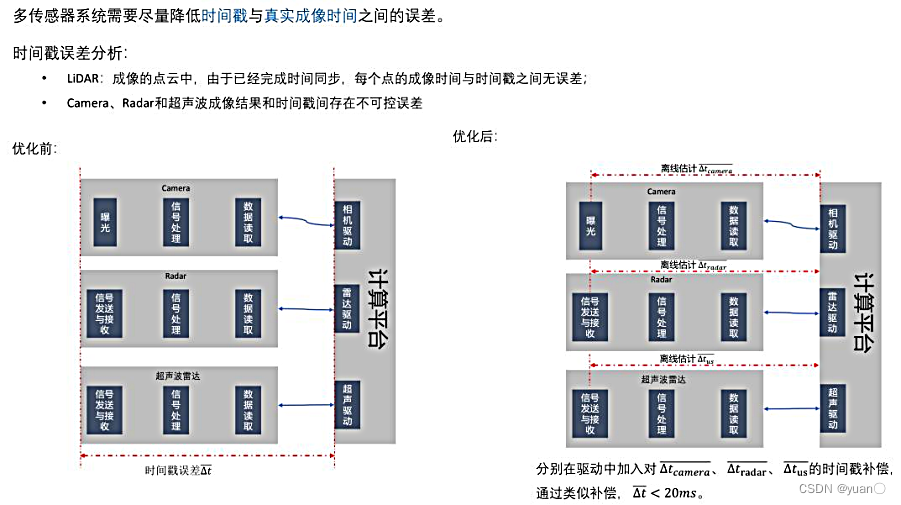
更进一步，让传感器同时成像（硬同步），可进一步降低成像误差。
构造一个触发装置，在指定的时刻，发送触发信号，让所有的传感器触发成像,减少成像时刻误差。该设备功能如下:
- 连接GPS信号和NTP server,确保时钟实现微秒级同步
- 设置触发逻辑(如LiDAR正 前方的成像相位)，同时触发LiDAR和Camera成像
- 支持多LiDAR和多Camera,暂不支持Radar和超声波雷达
优点:系统精度更高，可将系统同步精度控制在
Δ
\Delta
Δt < 5ms;
缺点:丢失一些系统的灵活度和高频数据。
5. 多传感器融合算法
5.1 多传感器融合问题建模
我们将多传感器融合问题如下建模：
对于建图与定位可以用以下式子描述：
G
(
s
e
n
s
o
r
t
)
→
{
[
R
t
0
1
]
t
,
{
l
a
n
d
m
a
r
k
s
0
,
.
.
.
,
l
a
n
d
m
a
r
k
s
t
}
}
G(senso{r_t}) \to \left\{ {{{\left[ {\begin{array}{ccccccccccccccc}R&t\\0&1\end{array}} \right]}_t},\left\{ {landmark{s_0},...,landmark{s_t}} \right\}} \right\}
G(sensort)→{[R0t1]t,{landmarks0,...,landmarkst}}
其中：
s e n s o r t sensor_t sensort为t时刻传感器系统采集的信息，通常包含 g n s s t , i m a g e s t , p o i n t l o u d t , . . . {gnss_t, images_t, pointloud_t,...} gnsst,imagest,pointloudt,...;R R R为当前自车坐标系相对于世界坐标系的旋转矩阵， t t t为对应的平移向量;l a n d m a r k s t landmarks_t landmarkst为 t t t时刻的道路环境特征元素，以语义或者特征点的形式表达;
对于感知问题，可以用以下式子描述：
F
(
s
e
n
s
o
r
t
)
→
{
o
b
j
e
c
t
s
t
,
o
b
j
e
c
t
=
{
x
,
y
,
z
,
l
,
w
,
h
,
v
x
,
v
y
,
v
z
,
.
.
.
}
s
c
e
n
a
r
i
o
s
t
,
s
c
e
n
a
r
i
o
=
{
c
l
a
s
s
,
z
o
n
e
}
.
.
.
\begin{array}{l}F(senso{r_t}) \to \left\{ \begin{array}{l}object{s_t},object = \{ x,y,z,l,w,h,{v_x},{v_y},{v_z},...\} \\scenario{s_t},scenario = \{ class,zone\} \\...\end{array} \right.\\\end{array}
F(sensort)→⎩⎨⎧objectst,object={x,y,z,l,w,h,vx,vy,vz,...}scenariost,scenario={class,zone}...
其中:
- sensort为t时刻传感器系统采集的信息，通常包含{gnsst, imagest, pointclouds.,-.};
- objectst为t时刻环境中的目标级障碍物，可用位置、速度、加速度、类别等属性描述独立个体;
- scenariot为t时刻环境中的语义级别元素描述，通常不能独立的障碍物形式表达，如施工区域、雨水场景等;
对于感知问题，有两种主要实现方式：前融合与后融合。
5.2 后融合
后融合：多模态数据分别完成检测和分割任务后的元素融合。
首先对LiDAR的数据进行3D检测与分割，再进行多目标跟踪，得到3D空间的元素；对camera的数据进行2D的检测，得到2D空间的元素信息；对RaDAR的信息进行处理。得到2.5D的信息，利用算法进行多传感器融合，最后输出结果。
5.2.1 后融合需要解决的问题
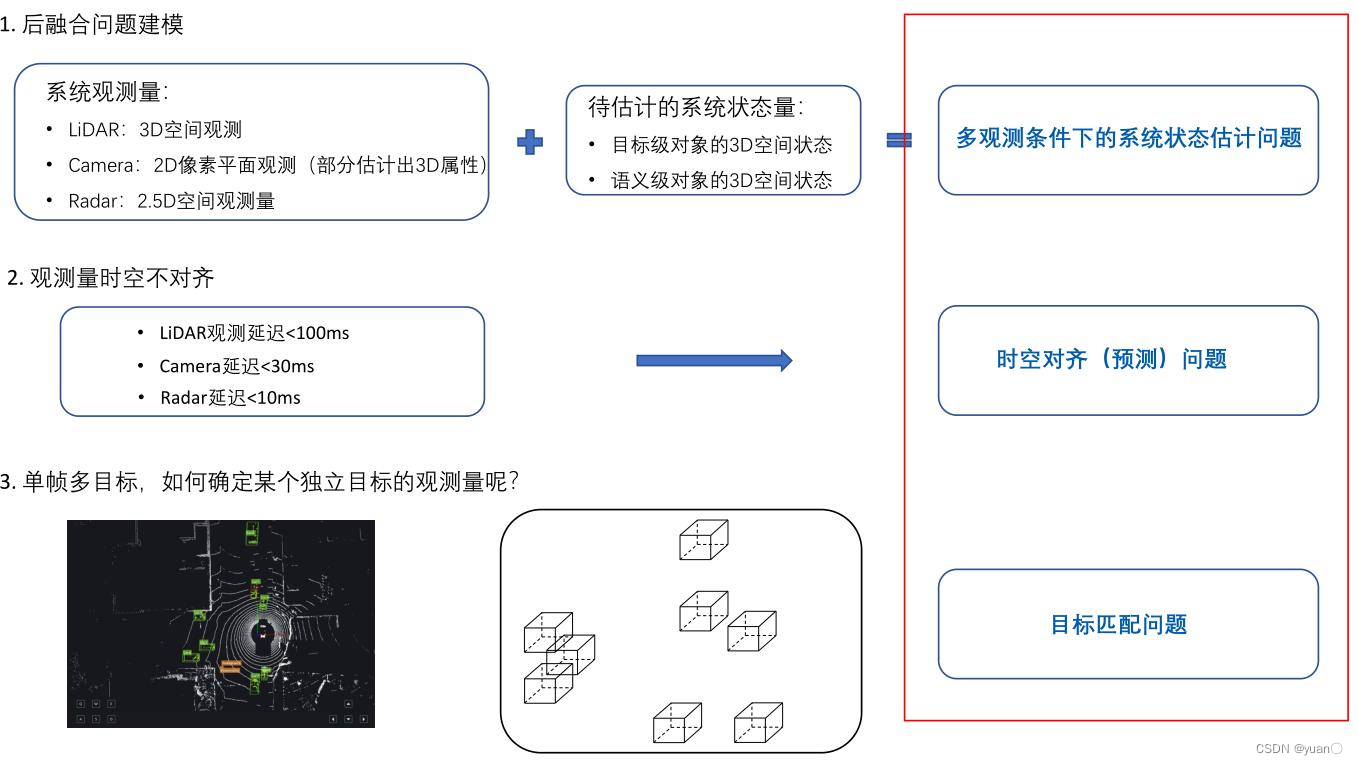后融合需要解决的问题主要有三个：
- 多观测条件下系统状态估计问题
- 时空对齐（预测）wenti
- 目标匹配问题
5.3 前融合
前融合(early fusion) :多模数据直接输入模型，让模型通过多模数据提升目标检测精度的融合方式。
多模态融合：
- 模态(modality) 是指信息的某种特定的表达形式，比如语音、图像或文本。
- Deep Learning是多模态融合的主要技术手段
5.3.1 前融合需要解决的问题
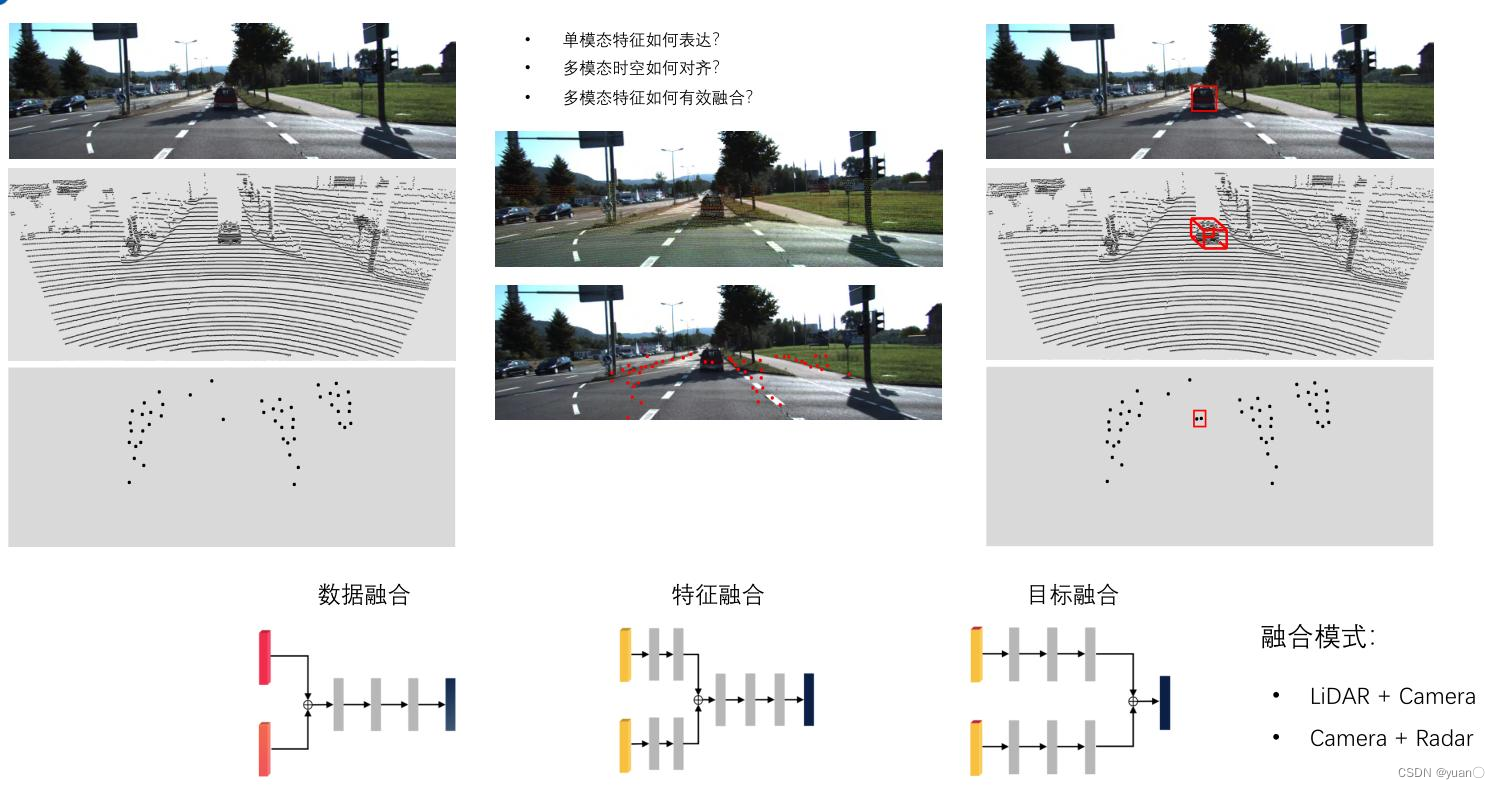
前融合需要解决的问题主要有三个：
- 单模态特征如何表达？
- 多模态时空如何对齐？
- 多模态特征如何有效融合？
5.3.2 数据融合、特征融合与目标融合
对于多模态融合，有三种常见方法：数据融合、特征融合以及目标融合。
要求原始数据时空对齐程度高，像素级和点级别的对齐
允许有一定程度的不对齐， 通常要求时间误差<10ms
允许有一定程度的不对齐，通常要求时间误差<10ms
目标融合数据融合特征融合方法各传感器输出目标级结果，然后融合各传感器原始数据融合，然后检测各传感预处理，得到特征级融合架构特点融合复杂度低（方便查看各传感器的效果），提升了感知的稳定性，但融合不充分，难以提升感知效果信息充分交互，在一定程度上提升感知能力，但过程复杂，对深度学习可能不友好既实现充分交互，又节省一定算力，保证每个传感器的特征有一定的独立性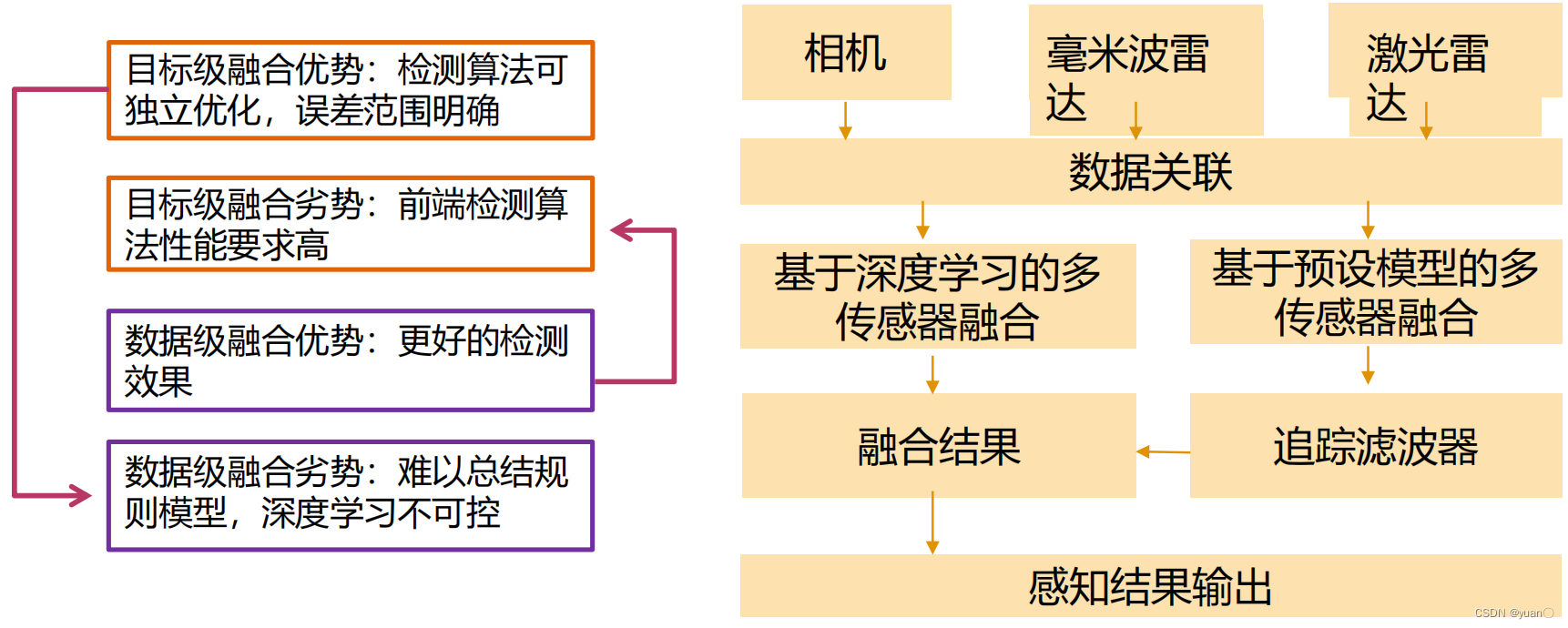
5.4 实际的多传感器融合的感知系统
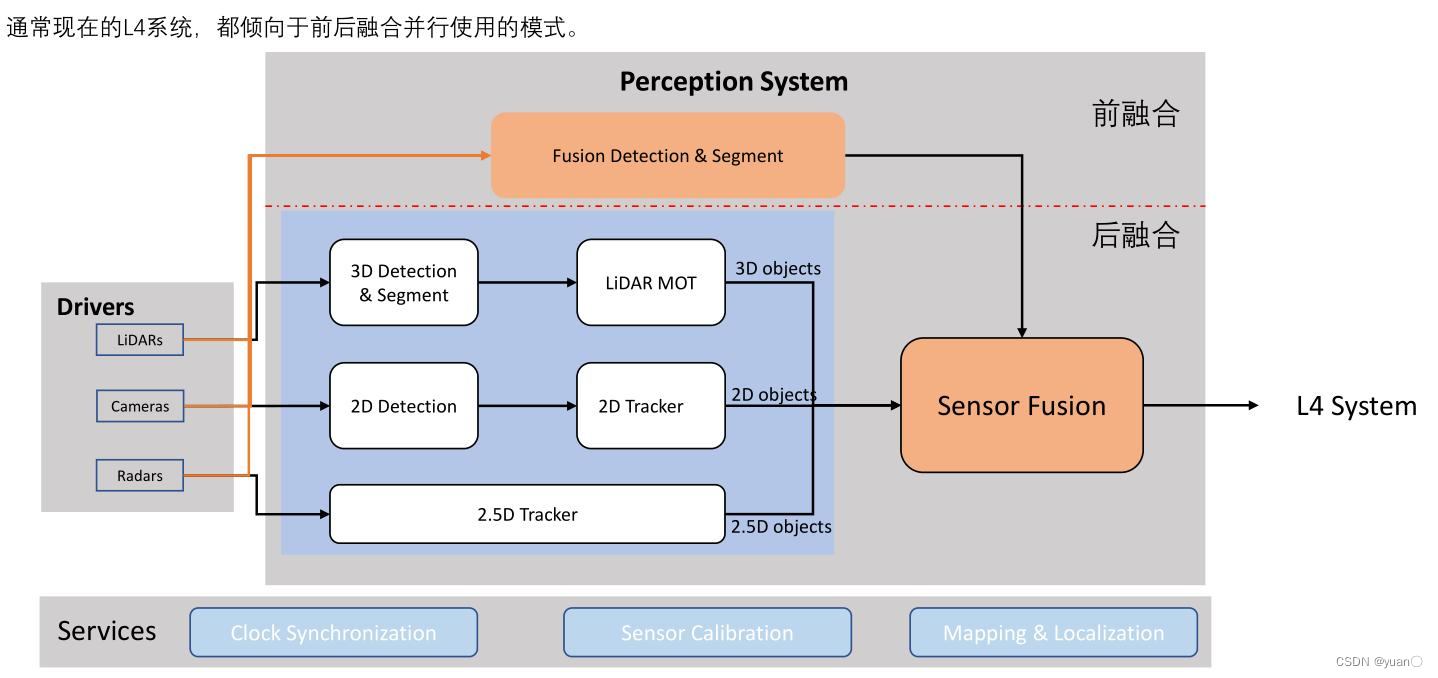
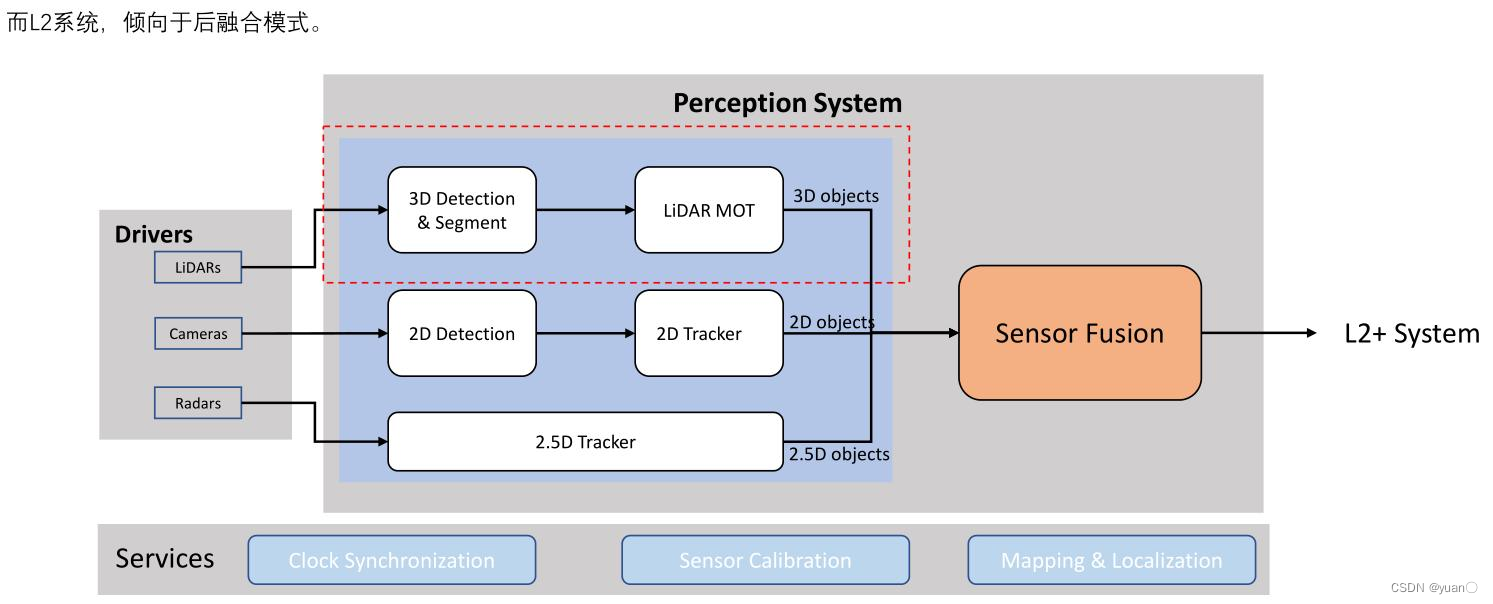
6. 状态空间表示法
6.1 动态系统的数学表达
状态变量：足以完全表征系统状态的最小个数的一组变量，记为
𝑥
1
(
𝑡
)
,
⋯
,
𝑥
𝑛
(
𝑡
)
𝑥_1 (𝑡) , ⋯ , 𝑥_𝑛 (𝑡)
x1(t),⋯,xn(t)
输入变量：表征系统输入信号的一组变量，也称控制变量，记为
𝑢
1
(
𝑡
)
,
⋯
,
𝑢
𝑙
(
𝑡
)
𝑢_1 (𝑡) , ⋯ , 𝑢_𝑙(𝑡)
u1(t),⋯,ul(t)
输出变量：表征系统输出信号的一组变量，也称观测变量，记为
y
1
(
𝑡
)
,
⋯
,
𝑦
𝑚
(
t
)
y_1 (𝑡) , ⋯ , 𝑦_𝑚 (t)
y1(t),⋯,ym(t)
以向量的形式表述时，对应的向量为状态向量𝒙(𝒕) ，控制向量𝒖(𝒕)，观测向量𝒚(𝒕)
状态方程： 描述状态向量动态特性的一阶微分方程组, 𝒘(𝒕)为过程噪声
x
˙
(
t
)
=
f
(
x
(
t
)
,
u
(
t
)
)
+
w
(
t
)
\dot x(t) = f(x(t),u(t)) + w(t)
x˙(t)=f(x(t),u(t))+w(t)
观测方程：描述状态向量与输出向量关系的方程组， 𝒗(𝒕)为观测噪声
y
(
t
)
=
h
(
x
(
t
)
,
u
(
t
)
)
+
v
(
t
)
y(t) = h(x(t),u(t)) + v(t)
y(t)=h(x(t),u(t))+v(t)
6.2 线性定常系统的数学表达
状态方程：
x
˙
(
t
)
=
A
′
x
(
t
)
+
B
′
u
(
t
)
+
w
(
t
)
\dot x(t) = A'x(t) + B'u(t) + w(t)
x˙(t)=A′x(t)+B′u(t)+w(t)
观测方程:
y
(
t
)
=
C
′
x
(
t
)
+
D
′
u
(
t
)
+
v
(
t
)
y(t) = C'x(t) + D'u(t) + v(t)
y(t)=C′x(t)+D′u(t)+v(t)
可控性：系统的所有状态都可由输入来影响控制，则称为可控系统；
可观性：系统的所有状态都可由输出来完全反映，则称为可观系统；
稳定性：系统自身特性，在偏离平衡状态的扰动消失后，返回原来平衡状态的能力
6.3 状态空间分析方法下多传感器融合问题的数学描述
状态方程：
x
k
+
1
=
A
x
k
+
B
u
k
,
协方差矩阵
Q
{x_{k + 1}} = A{x_k} + B{u_k},协方差矩阵Q
xk+1=Axk+Buk,协方差矩阵Q
观测方程：
y
k
+
1
=
C
x
k
+
1
+
D
u
k
+
1
,
协方差矩阵
R
{y_{k + 1}} = C{x_{k + 1}} + D{u_{k + 1}},协方差矩阵R
yk+1=Cxk+1+Duk+1,协方差矩阵R
各矩阵的物理意义
1，𝑨 叫作系统矩阵，或预测矩阵，𝑨 代表系统自身特性，如系统稳定性；
2，𝑩 叫作输入矩阵，或控制矩阵，𝑨与B共同决定系统可控性，B不一定满秩；
3，C 叫作输出矩阵，或观测矩阵，𝑨与 C共同决定系统可观性，C不一定满秩；
4，D 叫作直接转移矩阵，或前馈矩阵，代表输入直接影响测量值的特性
5，控制器角度：A,B,C,D 可以表征系统的传递函数。
6，观测器角度：B,D一般为零，因为可以将𝒖𝒌, 𝒖𝒌+𝟏看作是状态变量
7，Q,R为协方差矩阵，表示系统的不确定性
用多传感器构建系统的观测系统时，需符合以下假设：
1，系统输入、输出值都可获取， 即𝒖𝒌+𝟏，𝒚𝒌+𝟏为已知量；
2，系统参数矩阵均可获取， 即A,B,C,D都是已知量；
3，随机误差的概率分布已知， 即𝑸，𝑹为已知；
多传感器融合的数学本质：在输入、输出和状态空间已知的条件下，获取系统状态最优估计。
7. 卡尔曼滤波与扩展卡尔曼滤波
7.1 基于卡尔曼滤波的感知融合
7.1.1 卡尔曼滤波的特点
• KF之所以称为滤波，是因为它能从混杂信号中提取出所需信号，即一种排除随机干扰，提高测量精度的方法
• KF是一种时域递推算法，根据上一状态的估计值和当前状态的观测值推出当前状态，不需要存储大量的历史数据，便于计算机实现
构建卡尔曼滤波器的要点
• KF非常依赖于状态空间分析方法，即需要建立系统模型和观测模型
• KF是基于最小方差准则推导出来的一种线性滤波器，假定过程噪声和观测噪声均为高斯白噪声
7.1.2 传感器信息与模型知识的融合
7.1.3 KF卡尔曼滤波器的算法结构
7.1.4 卡尔曼滤波的启示与局限性
卡尔曼滤波的启示
• 将多传感器融合的抽象概念，转换为参数估计的数学问题，即利用多次测量值，来获得状态的最优估计
• 可以用方差作为信息质量的指标，并依此进行加权平均。方差越大，不确定性越高，信息的比重越小
• 回归计算，对于处理时间序列数据具有很多优势，数据储存量小，数据计算量小，数据利用率高
卡尔曼滤波的局限性
• 要求是线性系统→建模时需要构建A,C的形式
• 要求高斯白噪声→方差计算和传递使用了高斯分布特性
• 要求信息可建模→所有待融合信息都必须转化为方程组
7.2 基于扩展卡尔曼滤波的感知融合
7.2.1 非线性系统的多传感器融合
7.2.2 EKF扩展卡尔曼滤波器的算法结构
7.2.3 扩展卡尔曼滤波的启示与局限性
扩展卡尔曼滤波的启示
• 将多传感器融合的抽象概念，转换为参数估计的数学问题，即利用多次测量值，来获得状态的最优估计
• 可以用方差作为信息质量的指标，并依此进行加权平均。方差越大，不确定性越高，信息的比重越小
• 回归计算，对于处理时间序列数据具有很多优势，数据储存量小，数据计算量小，数据利用率高
• 可以近似处理非线性系统
扩展卡尔曼滤波的局限性
• 要近似线性系统→建模时需要求解雅可比矩阵
• 要求高斯白噪声→方差计算和传递使用了高斯分布特性
• 要求信息可建模→所有待融合信息都必须转化为方程组
8. Apollo文心大模型在自动驾驶中的应用
百度Apollo Day｜王井东：大模型已经成为自动驾驶能力提升核心驱动力
声明
本人所有文章仅作为自己的学习
记录，若有侵权，联系立删。本系列文章主要参考了清华大学、北京理工大学、哈尔滨工业大学、深蓝学院、百度Apollo等相关课程。
版权归原作者 yuan〇 所有， 如有侵权，请联系我们删除。