【图论】—— 最近公共祖先（LCA）

给定一颗树，若节点 z 既是节点 x 的祖先，也是节点 y 的祖先，那么称 z 为 x、y 的公共祖先。

在 x、y 的所有公共祖先中，深度最大的一个称为 x、y 的最近公共祖先，也称 LCA(x, y)

**LCA(x, y) **是 x 到根的路径与 y 到根的路径的交汇点。它也是 x 与 y 之间的路径上深度最小的节点。

树上倍增法

树上倍增法是一种很重要的算法。除了求 **LCA **外，它在很多问题中都有广泛的应用。

设 $fa[i,j]$ 表示 $x$ 的 $2^{k}$ 辈祖先，即从 $x$ 向根节点走 $2^{k}$ 步所到达的节点。

特别地，如果该节点不存在，则令 $fa[x, k]=0$ 。 $fa[x, 0]$ 就是 $x$ 的父节点。

除此之外， ![\large fa[x,k]=fa[fa[x,k-1],k-1]](https://latex.codecogs.com/gif.latex?%5Clarge%20fa%5Bx%2Ck%5D%3Dfa%5Bfa%5Bx%2Ck-1%5D%2Ck-1%5D) 。

这类似于一个动态规划的过程，“阶段”就是节点的深度。因此，我们可以对树进行广度优先遍历，按照层次顺序，在节点入队之前，计算它在 $\large fa$ 数组中对应的值。

以上是预处理，时间复杂度为 $\large O(nlogn)$ ，之后可以多次对不同的 x, y 计算 LCA，每次查询的复杂度是 $\large O(logn)$ 。

基于 $\large fa$ 数组计算** LCA(x,y)**，分为以下几步：

设 $depth[x]$ 表示 $x$ 的深度。不妨设 $depth[x]\geqslant depth[y]$ （否则可交换x, y）

用二进制拆分思想，把 $x$ 向上调整到和 $y$ 同一深度具体来说，就是依次尝试 $x$ 向上走 $k=2^{logn},\cdots 2^1,2^0$ 步，检查到达的节点是否是比 $y$ 深。在每次检查中，若是，则令 $x=fa[x,k]$

若 x = y, 说明已经找到了 LCA, LCA = y

用二进制拆分思想，把 $x$ 和 $y$ 同时向上调整，并保持深度一致且二者不会相会。具体来说，就是依次尝试把 x, y 同时向上走 $k=2^{logn},\cdots 2^1,2^0$ 步，在每次尝试中，若 $fa[x,k] \neq fa[y,k]$ （即仍未相会），则令 $x=fa[x,k], y = fa[y,k]$

此时 x, y 必定只差一步就相会了，它们的父节点 $fa[x,0]$ 就是** LCA**

例题讲解：AcWing 1172. 祖孙询问

细节1：设置哨兵
     如果从 i 开始跳 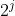![2^j](https://latex.codecogs.com/gif.latex?2%5Ej) 步会跳过根节点，那么 ![fa[i,j]=0,depth[0]=0](https://latex.codecogs.com/gif.latex?fa%5Bi%2Cj%5D%3D0%2Cdepth%5B0%5D%3D0)
细节2：边的数量 M 需要是点的数量 N 的两倍（无向边需要连两次）

预处理出所有的 fa[][] 和 depth[]

void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    int hh = 0, tt = 0;
    q[0] = root;
    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q[ ++ tt] = j;
                fa[j][0] = t;
                for (int k = 1; k <= 15; k ++ )
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
            }
        }
    }
}

LCA算法

int lca(int a, int b)
{
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k -- )
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
    if (a == b) return a;
    for (int k = 15; k >= 0; k -- )
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    return fa[a][0];
}

AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 40010, M = N * 2;

int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][16];
int q[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 预处理出所有的 fa 和 depth
void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    int hh = 0, tt = 0;
    q[0] = root;
    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q[ ++ tt] = j;
                fa[j][0] = t;
                for (int k = 1; k <= 15; k ++ )
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
            }
        }
    }
}

int lca(int a, int b)
{
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k -- )
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
    if (a == b) return a;
    for (int k = 15; k >= 0; k -- )
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    return fa[a][0];
}

int main()
{
    scanf("%d", &n);
    int root = 0;
    memset(h, -1, sizeof h);

    for (int i = 0; i < n; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        if (b == -1) root = a;
        else add(a, b), add(b, a);
    }

    bfs(root);

    scanf("%d", &m);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        int p = lca(a, b);
        if (p == a) puts("1");
        else if (p == b) puts("2");
        else puts("0");
    }

    return 0;
}

向上标记法

从 x 向上走到根节点，并标记所有经过的结点

从 y 向上走到根节点，当第一次遇到已标记的节点时，就找了 LCA(x,y)

对于每个询问，向上标记法的时间复杂度最坏为 $O(n)$

LCA的Tarjan算法

Tarjan算法本质上使用并查集对于“向上标记法”的优化。

它是一个离线算法，需要把 m 个操作一次性读入，统一计算，最后统一输出。

时间复杂度是 $O(m + n)$ 。

在深度优先遍历的任意时刻，树中节点分为三类：

已经完成访问完毕并且回溯的节点。在这些节点上标记一个整数2

已经开始递归，但尚未回溯的节点。这些节点就是当前正在访问的节点 $x$ 以及 $x$ 的祖先。在这些节点上标记一个整数1。

尚未访问的节点，这些节点没有标记

对于正在访问的节点 $x$ ，它到根节点的路径已经标记为 1。若 $y$ 已经是访问完毕并且回溯的节点，则 $LCA(x,y)$ 就是从 $y$ 向上走到根，第一个遇到的标记为 1 的点。

可以利用并查集进行优化，当一个节点获得整数 2 的标记时，把它所在的集合合并到它的父节点所在的集合中（合并时它的父节点一定为 1，并且单独构成一个集合）。

这相当于每个完成回溯的节点都有一个指针指向它的父节点，只需要查询 $y$ 所在的集合的代表元素（并查集的 $find$ 操作），等价于从 $y$ 向上一直走到一个开始递归但尚未回溯的节点（具有标记1），即 $LCA(x,y)$

如下图所示：

例题：AcWing 1171. 距离

核心思想： $ans = dist[x] + dist[y] - 2 * dist[LCA(x,y)]$

AC代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;

typedef pair<int, int> PII;

const int N = 20010, M = 2 * N;

int n, m;
int h[N], e[M], w[N], ne[M], idx;
int p[N];
int dist[N];   
int st[N];  // 标记数组(分三类)
int res[N];

// first 存查询的另外一个点, second 存查询编号
vector<PII> query[N];

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}

// 确定每个点到1号点的距离
void dfs(int u, int fa)
{
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        // 判断是否是u的父节点
        if(j == fa) continue;
        dist[j] = dist[u] + w[i];
        dfs(j, u);
    }
}

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void tarjan(int u)
{
    // 当前正在搜索的点
    st[u] = 1;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            tarjan(j);
            p[j] = u;
        }
    }
    
    for(auto item: query[u])
    {
        int y = item.first, id = item.second;
        if(st[y] == 2)
        {
            int anc = find(y);
            res[id] = dist[u] + dist[y] - dist[anc] * 2;
        }
    }
    
    st[u] = 2;
}

int main()
{
    cin >> n >> m;
    memset(h, -1 , sizeof h);
    for(int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    
    // 初始化并查集数组
    for(int i = 1; i <= n; i ++ ) p[i] = i;
    
    for(int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        if(a != b)
        {
            query[a].push_back({b, i});
            query[b].push_back({a, i});
        }
    }
    
    dfs(1, -1);
    tarjan(1);
    
    
    for(int i = 0; i < m; i ++ ) cout << res[i] << endl;
    return 0;
}

标签：图论蓝桥杯数据结构

本文转载自: https://blog.csdn.net/forever_bryant/article/details/125321286
版权归原作者 玄澈_ 所有，如有侵权，请联系我们删除。

【图论】—— 最近公共祖先（LCA）

树上倍增法

例题讲解：AcWing 1172. 祖孙询问

预处理出所有的 fa[][] 和 depth[]

LCA算法

AC代码

向上标记法

LCA的Tarjan算法

例题：AcWing 1171. 距离

AC代码

发表评论