毕业设计-基于 MATLAB 的工业机器人运动学分析与实现

前言

 📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。

🚀对毕设有任何疑问都可以问学长哦!

选题指导: https://blog.csdn.net/qq_37340229/article/details/128243277

大家好,这里是海浪学长毕设专题,本次分享的课题是

🎯基于 MATLAB 的工业机器人运动学分析与仿真

课题背景和意义

工业机器人作为智能制造业中不可替代的重要装备和手段，已成为衡量一个国家制造业水平和科技水平的重要标志。华数 HSR-JR605 型机器人是我校“1+X”工业机器人应用编程初级和中级的主要设备，在实际操作过程中，机器人要完成预定的搬运和码垛等任务，就必须知道末端执行器在目标点的位置和姿态，需要实现工业机器人末端执行器空间运动轨迹的控制。末端执行器的在基坐标
中的空间位姿这个运动学问题则是实现对机器人控制首先要解决的问题。为更有效的探索工业机器人运动学的研究方法，以 HSR-JR605 工业机器人作为研究对象，在 MATLAB 环境下利用仿真技术对机器人的工作进行模拟，运用 MatlabToolbox V9.10 工具箱构建机器人运动学三维仿真模型，进行正、逆运动学仿真和轨迹规划，掌握各个关节的角度、速度和加速度的变化规律，为机器人后期开发和研究提供一种试验分析手段和理论支持。

实现技术思路

一、机器人的工作空间

机器人的工作空间，一般用水平面和垂直面的投影表 示，代表着机器人末端执行器的活动范围，用于指定参考 点（第五轴的轴心）根据设计极限所能达到的可能的区域。 合理制定的机器人工作空间有利于机器人充分发挥其工 作能力，合理安排机器人和工件的相对位置，避免出现末端执行器不能到达工作死区等问题，是评价机器人工作能 力的一个重要的运动学指标，也是机器人在控制和应用过 程中首先需要考虑的关键问题。

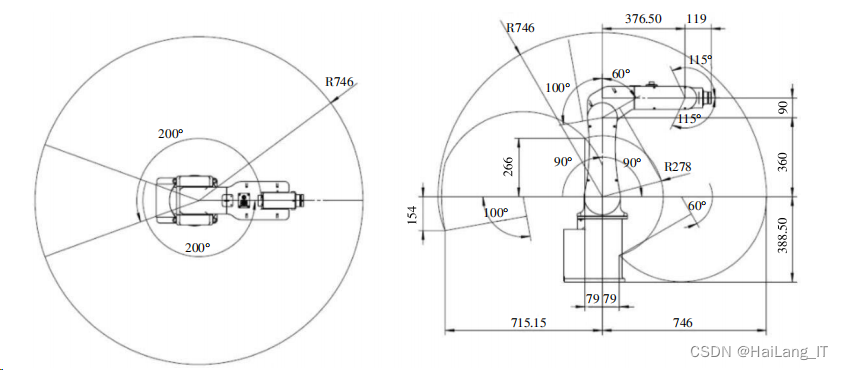
二、HSR-JR605 型工业机器人的结构及连杆参数

HSR-JR605 型工业机器人是典型的垂直多关节式机 器人，有 6 个旋转关节，具有 6 个自由度，为便于分析和建 模，机器人可视为由 6 个连杆被关节按顺序连接而成。其 中，腰关节 1、大臂和肩关节组成的关节 2、小臂和肘关节 组成的关节 3 控制着机器人末端执行器手腕的空间位置， 和由关节 4、5、6 组成的腕关节控制着机器人末端执行器 手腕的姿态。

D-H 参数法参数法是 Denavit 和 Hartenberg 于 1955 年提出的一种为关节链中的每一个杆连杆建立固定坐标 系的矩阵方法，用齐次坐标变换矩阵来描述坐标系变换相 对位姿的变化，对连杆 i 建立坐标系{i}，{i}的 z 轴与关节 i 的轴线重合，{i} 的 x 轴沿着两个关节 i 和 i+1 轴线的公垂线。HSR-JR605 型工业机器人各关节坐标系如图所示。

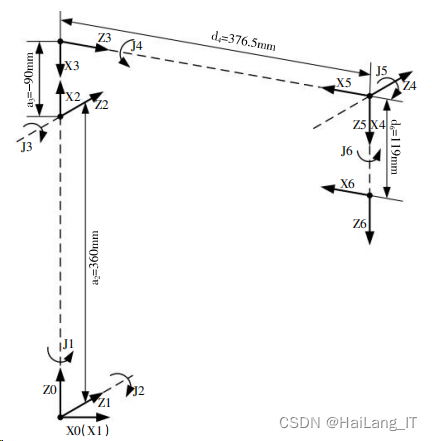
综合图所示的工作空间和机构尺寸，采用机器人坐标系前置（第 i 个坐标系建立在第 i 关节轴上）的 D-H 参数表示法，HSR-JR605 型工业机器人 D-H 参数如表所示。

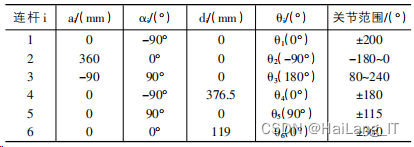
三、建立 HSR-JR605 型工业机器人的运动学方程

为建立运动学方程，首先需要写出相邻杆件的位姿矩 阵，用齐次变换矩阵 Ai 表示连杆 i 坐标是在连杆 i+1 坐标 系中的位姿，在 D-H 参数法中，每个齐次变换矩阵 Ai 都 可以表示为四个基本矩阵的乘积，如下所示：

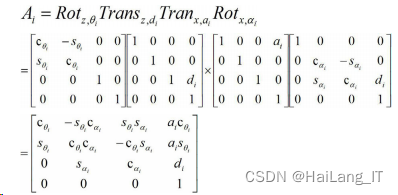
根据建立的 HSR-JR605 型工业机器人 D-H 坐标系如图所示，各连杆参数见表 1，则 HSR-JR605 型工业机 器人六个杆件的齐次变换矩阵分别为：

该矩阵是 4伊4 齐次变换矩阵，矩阵中各元素是在带入 D-H 参数表中的参数后的求出的如下表达式：

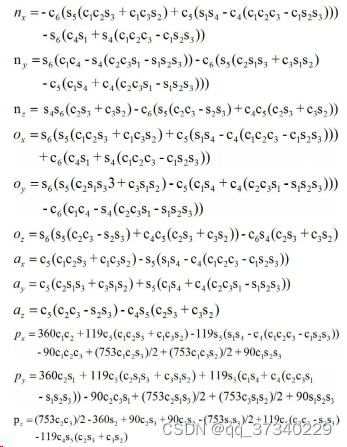
四、基于 MATLAB 的 HSR-JR605 型工业机器人的 运动学仿真

通过上述分析，运动学方程的需要大量的计算，给分 析和设计工作带来了很大的不便，为解决这些问题我们引 入计算机技术，应用 Matlab 2017a 及机器人工具箱 Matlab Toolbox V9.10 两个仿真软件在 D-H 参数表的基础上首先 构建 HSR-JR605 型工业机器人仿真模型。

利用 Link 和 SerialLink 功能函数构建机器人仿真模型

创 建 机 器 人 的 两 个 最 重 要 的 函 数 是 ：Link 和 SerialLink [6]。Link 函数的调用格式为 L=Link（[theta D A alpha],‘standard’），功能是创建一个带默认参数的连杆，6 个函数构建出机器人的 6 个连杆，应用 SerialLink 函数将 6 个连杆进行连接，构建 HSR-JR605 型工业机器人程序 如下：

程序中，pi 代表 仔，teach 函数的功能是驱动机器人，并生成滑块 q1耀q6 控制机器人运动，类似于机器人示教器，使仿真机器人更生动直观。

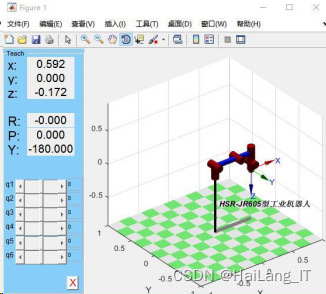
**利用 fkine 和 ikine 功能函数进行机器人正、逆运动学仿真 **

在构建好机器人三维仿真模型的基础上，首先进行正动学分析，已知 D-H 参数如表 1，假设其 6 个关节变量 分别为：0、pi/2、0、0、pi、0，Matlab Toolbox V9.10 软件中的 fkine 功能函数可以实现机器人运动学正问题的求解，程 序如下。

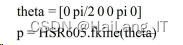
运行结果为：

在正运动学仿真结果的基础上，已知末端执行器相对 于基坐标的位姿为仿真结果 p，使用 ikine 功能函数可以 实现机器人逆运动学问题的求解，即求出假设的 6 个关节 变量。同时，若仿真结果和假设关节变量相同，则可得出构 建的工业机器人三维仿真模型完全正确。逆运动学求解程 序如下。

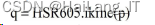
运行结果为：

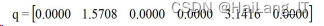
q 为 HSR-JR605 型工业机器人末端执行器位姿为 p 时各关节变量，q=theta，证明在 Matlab Toolbox V9.10 软件 构建 HSR-JR605 型工业机器人三维仿真模型完全正确。

利用 jtraj 功能函数进行轨迹规划仿真

仿真以点对点（PTP）运动的轨迹规划为 例，默认起始和终止速度均为 0，选择机器人的机械原点 p1=[0 -pi/2 pi 0 pi/2 0]点为轨迹起始点，p2=[pi pi/2 pi/3 pi/4 pi/5 pi/6]为轨迹目标点，为采样轨迹运动过程中各个 关节的位姿、速度和加速度，应用仿真软件中的 jtraj 功能 函数进行差值计算，jtraj 功能函数采用的是 7 次多项式插 值法，选取的时间范围为 t=0耀5s，插值步长为 0.1s，轨迹规 划程序如下。

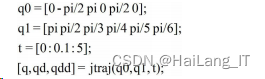
利用机器人工具箱中的subplot 和 qplot 函数以三维动画的形式演示整个运动过程。

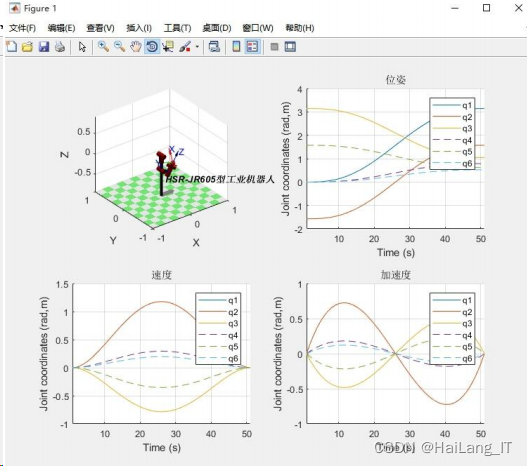
运行后可得到各关节的位姿、关节速度、关节加速度 的仿真曲线如图所示。 位姿曲线表明了 6 个关节的位姿在运动过程中能实 现协调联动，关节速度和加速度曲线无断点、不存在奇异 点，连续平滑，表明机器人在启动、加速、减速和停止动作 时柔性较好，轨迹精度高。

重要代码

1、startup_rvc还是不能少的，先启动工具箱。

 startup_rvc

2、首先定义机械臂连杆参数，参考上面的D-H模型，即可把机械臂建模出来。工具箱中采用的是Link函数，里面的五个参数分别对应着：关节角theta，连杆偏移d，连杆长a，连杆扭角alpha和关节类型sigma。定义好之后，可以通过L1.X来获取参数。比如，若Ln的杆长是0.3，那么输入Ln.a就会输出0.3。

%        theta     d       a        alpha     sigma
L1 = Link([0       0       0         0         0     ]); % 定义连杆的DH参数

3、qlim可以用来定义每个轴的旋转限度，比如如果第一个轴旋转角度限制为[-pi/6,pi/6]，那么即可输入。

L1.qlim=[-pi/6,pi/6];

4、当每个轴都定义好后，可以定义机械臂Rob，使用函数SerialLink。比如，一个七轴机械臂的定义方式就是

Rob=SerialLink([L1 L2 L3 L4 L5 L6 L7], 'name', '机械臂', 'base',transl(0,0,0.2)*troty(pi/2));

5、采用plot函数，能观察在规定各个轴旋转条件下，机械臂的形状。比如，让每个轴旋转pi/6或者-pi/6。

Rob.plot([pi/6,pi,pi/6,pi/6,-pi/6,-pi/6,-pi/6])

6、工具箱里有示教模式，可以用teach函数看到结果。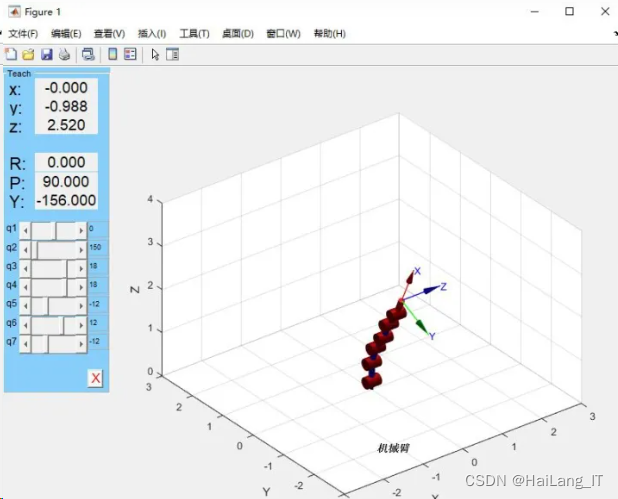

示教模式中可以通过调节q1-q7去实时改变机械臂的每个轴的转角，上方的x，y，z代表机械臂末端的空间坐标；R，P，N则代表最终位置的旋转、偏移、姿态角。

7、fkine函数是前向动力学函数，通过给定机械臂的各轴角度，可以计算到转动最后位置的44矩阵（最前面所讲的44矩阵）。比如

T = Rob.fkine([pi/6,pi/6,pi/6,pi/6,-pi/6,-pi/6,-pi/6)]

就是计算各个关节角是指定角度的时候，机械臂头的6DOF信息。

8、最后是反向动力学函数，使用ikine对于4*4的矩阵，即机械臂头的6DOF信息反推各个关节的角度。计算的结果不一定准确，但一般来说，此工具箱的IK做到了尽量防止机械臂之间轴的扭曲。测试可以采用7中算出来的结果。

qi = Rob.ikine(T)

9、完整的汇总一下大概就是

clear L
warning off
%        theta     d       a        alpha     sigma
L1 = Link([0       0       0         0         0     ]); % 定义连杆的DH参数
L2 = Link([pi      0       0.43      0         0     ]);
L3 = Link([ 0      0       0.43      0         0     ]);
L4 = Link([ 0      0       0.43      0         0     ]);
L5 = Link([ 0      0       0.43      0         0     ]);
L6 = Link([ 0      0       0.43      0         0     ]);
L7 = Link([ 0      0       0.43      0         0     ]);
 
% 限制转动角度
L1.qlim=[-pi/6,pi/6];
L2.qlim=[pi*5/6,pi];
L3.qlim=[-pi/6,pi/6];
L4.qlim=[-pi/6,pi/6];
L5.qlim=[-pi/6,pi/6];
L6.qlim=[-pi/6,pi/6];
L7.qlim=[-pi/6,pi/6];
L8.qlim=[-pi/6,pi/6];
 
Rob=SerialLink([L1 L2 L3 L4 L5 L6 L7], 'name', '机械臂', 'base',transl(0,0,0.2)*troty(pi/2));
q0 = [pi/6,pi,pi/6,pi/6,-pi/6,-pi/6,-pi/6];    % 设置输出时的theta姿态，初始为竖直状态
 
Rob.teach;
result = Rob.getpos(); % 调节完成后按X，可得到调后的变量
axis([-3 3 -3 3 0 4])
Rob.plot(q0);
disp("D-H参数表及其他参数：")
Rob.display();
 
% 运动学正解：根据关节角结算出末端位姿
T = Rob.fkine([pi/6,pi,pi/6,pi/6,-pi/6,-pi/6,-pi/6]);
 
% 运动学逆解：根据末端位姿结算出关节角
qi = Rob.ikine(T);
disp('根据关节角，计算末端位姿：')
disp(T)
disp('根据末端位姿，计算关节角：')
disp(qi)

10、以上就是机械臂的一些基础知识，以及rvc-tools的基本使用了。

实现效果图样例

机器人系统集成应用：

我是海浪学长,创作不易,欢迎点赞、关注、收藏、留言。

毕设帮助，疑难解答，欢迎打扰！

最后