数学建模--预测类模型

一、中短期预测

1、灰色预测法

灰色预测模型（ Gray Forecast Model ）是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。当我们应用运筹学的思想方法解决实际问题，制定发展战略和政策、进行重大问题的决策时，都必须对未来进行科学的预测。预测是根据客观事物的过去和现在的发展规律，借助于科学的方法对其未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。

①适用范围

适用范围：该模型使用的不是原始数据的序列，而是生成的数据序列。核心体系是Grey Model，即对原始数据作累加生成（或其他处理生成）得到近似的指数规律再进行建模的方法。

优点：在处理较少的特征值数据，不需要数据的样本空间足够大，就能解决历史数据少、序列的完整性以及可靠性低的问题，能将无规律的原始数据进行生成得到规律较强的生成序列。

缺点：只适用于中短期的预测，只适合近似于指数增长的预测。

②模型实现

GM(1,1)模型适用于具有较强指数规律的序列，只能描述单调的变化过程，而 Verhulst 模型则适用于非单调的摆动发展序列或具有饱和状态的 S 形序列。下面对比一下两种方法：

用matlab语言采用Verhulst模型预测

clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37 7.39 7.81 8.35 9.39 10.59 10.94 10.44];
n=length(x1);
nian=1990:2003;
plot(nian,x1,'o-');
x0=diff(x1);
x0=[x1(1),x0]
for i=2:n
    z1(i)=0.5*(x1(i)+x1(i-1));
end
z1
B=[-z1(2:end)',z1(2:end)'.^2]
Y=x0(2:end)'
abhat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b*x^2','x(0)=x0'); %求解常微分方程
x=subs(x,{'a','b','x0'},{abhat(1),abhat(2),x1(1)}); %代入参数值
yuce=subs(x,'t',0:14) %计算预测值
digits(6); x=vpa(x) %显示微分方程的解，为了提高计算精度，把该语句放在计算预测值之后，或者不使用该语句
yuce(16)=yuce(15);
x1_all=[x1,9.92,10.71];
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(1); %数据列的始点零化像
yuce_0=yuce-yuce(1); %数据列的始点零化像
s0=abs(sum(x1_all_0(1:end-1))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(1:end-1))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(1:end-1))+0.5*tt(end));
absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,1)/std(x1_all,1) %计算标准差比值

参考文章：http://t.csdn.cn/OIMNK![](https://img-blog.csdnimg.cn/03d63a5253d4448f8b2307c48389842c.png)参考文章：http://t.csdn.cn/OIMNK

用python语言采用GM(1,1）微分方程预测

import numpy as np
import math
history_data = [4.93, 5.33, 5.87, 6.35, 6.63, 7.15, 7.37, 7.39, 7.81, 8.35,
                9.39, 10.59, 10.94, 10.44]
n = len(history_data)
X0 = np.array(history_data)
# 累加生成
history_data_agg = [sum(history_data[0:i + 1]) for i in range(n)]
X1 = np.array(history_data_agg)
# 计算数据矩阵B和数据向量Y
B = np.zeros([n - 1, 2])
Y = np.zeros([n - 1, 1])
for i in range(0, n - 1):
    B[i][0] = -0.5 * (X1[i] + X1[i + 1])
    B[i][1] = 1
    Y[i][0] = X0[i + 1]
# 计算GM(1,1)微分方程的参数a和u
# A = np.zeros([2,1])
A = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
a = A[0][0]
u = A[1][0]
# 建立灰色预测模型
XX0 = np.zeros(n)
XX0[0] = X0[0]
for i in range(1, n):
    XX0[i] = (X0[0] - u / a) * (1 - math.exp(a)) * math.exp(-a * (i));
# 模型精度的后验差检验
e = 0  # 求残差平均值
for i in range(0, n):
    e += (X0[i] - XX0[i])
e /= n
# 求历史数据平均值
aver = 0;
for i in range(0, n):
    aver += X0[i]
aver /= n
# 求历史数据方差
s12 = 0;
for i in range(0, n):
    s12 += (X0[i] - aver) ** 2;
s12 /= n
# 求残差方差
s22 = 0;
for i in range(0, n):
    s22 += ((X0[i] - XX0[i]) - e) ** 2;
s22 /= n
# 求后验差比值
C = s22 / s12
# 求小误差概率
cout = 0
for i in range(0, n):
    if abs((X0[i] - XX0[i]) - e) < 0.6754 * math.sqrt(s12):
        cout = cout + 1
    else:
        cout = cout
P = cout / n
if (C < 0.35 and P > 0.95):
    # 预测精度为一级
    m = 2  # 请输入需要预测的年数
    # print('往后m各年负荷为：')
    f = np.zeros(m)
    for i in range(0, m):
        f[i] = (X0[0] - u / a) * (1 - math.exp(a)) * math.exp(-a * (i + n))
        print(f[i])
else:
    print('灰色预测法不适用')

2、回归分析

①适用范围

回归分析是研究变量之间因果关系的一种统计模型；因变量就是结果，自变量就是原因；基于结果变量（因变量）的种类，回归分析可分为：线性回归（因变量为连续变量）、logistic回归（因变量为分类变量）、柏松回归（因变量为计数变量）；这三种回归模型中自变量则可以是任意类型的变量。

有的自变量对因变量的影响不是很大，且自变量之间可能存在多重共线性（即可能不完全独立），通过建立逐步回归分析，进行X因子筛选。

比如：收入水平于受教育程度、所在行业、工作年限、工作种类的关系；公路客运量与人口增长量、私家车保有量、国民生产总值、国民收入等因素的关系。

②模型实现

几种回归分析的matlab代码如下

非线性回归

%% 非线性回归
clc, clear
x0 = [1  8.55  470  300  10
    2  3.79  285  80  10
    3  4.82  470  300  120
    4  0.02  470  300  120
    5  2.75  470    80   10
    6 14.39  100  190  10
    7  2.54   100   80   65
    8  4.35   470  190  65
    9    13  100  300  54
    10  8.5  100  300  120
    11  0.05  100  80  120
    12  11.32  285  300  10
    13  3.13  285  190  120];
x = x0(:, 3:5);
y = x0(:, 2);
% 参数的初始预估值
beta = [0.1, 0.05, 0.02, 1, 2]';
[betahat, r, j] = nlinfit(x, y, @func, beta);
betaci = nlparci(betahat, r, 'jacobian', j);
% 回归系数以及置信区间
betaa = [betahat, betaci];
% y的预测值以及置信区间半径
[yhat, delta] = nlpredci(@func, x, betahat, r, 'jacobian', j);
% 绘制交互式画面
nlintool(x, y, 'func', beta)

** 逐步回归模型**

%% 逐步回归模型
clc, clear
x0 = [1  8.55  470  300  10
    2  3.79  285  80  10
    3  4.82  470  300  120
    4  0.02  470  300  120
    5  2.75  470    80   10
    6 14.39  100  190  10
    7  2.54   100   80   65
    8  4.35   470  190  65
    9    13  100  300  54
    10  8.5  100  300  120
    11  0.05  100  80  120
    12  11.32  285  300  10
    13  3.13  285  190  120];
x = x0(:, 3:5);
y = x0(:, 2);
stepwise(x, y)

** 一元多项回归模型**

%% 一元多项式回归模型
% 选取 y = a2*x^2 + a1*x + a0
clc, clear
x0 = 17: 2: 29;
y0 = [20.48, 25.13, 26.15, 30.0, 26.1, 20.3, 19.35];
[p, s] = polyfit(x0, y0, 2);  % 2表示阶数
p                                              % p返回a2，a1，a0三个参数
% 求polyfit所得的回归多项式在x0处的预测值Y
%及预测值的显著性为1-alpha的置信区间DELTA；
%alpha缺省时为0.05。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数
[y, delta] = polyconf(p, x0, s);   % delta为置信区间半径
polytool(x0, y0, 2)

多元二项式回归

%% 多元二项式回归
% rstool(x, y, model, alpha) 
% model有四种：线性，纯二次，交叉，完全二次
clc, clear
x1 = [120 140 190 130 155 175 125 145 180 150]';
x2 = [100 110    90 150 210 150 250 270 300 250]';
y   = [102  100 120  77 46  93  26  69  65  85]';
x = [x1 x2];
rstool(x, y, 'purequadratic')

一元（多元）线性回归

%% 一元（多元）线性回归
%x = input('输入需要预测的一组数据:(如[0.10 0.11 0.12 ...)\n');
% 测试用例：
x1 = [0.1:0.01:0.18]';
%y = input('输入需要预测的一组数据:(如[0.10 0.11 0.12 ...)\n');
% 测试用例：
y = [42, 41.5, 45.0, 45.5, 45.0, 47.5, 49.0, 55.0, 50.0]';
plot(x1, y, '+')  % 观察是否近似为线性模型
x = [ones(9, 1), x1];
[b, bint, r, rint, stats] = regress(y, x);
b                         %回归系数估计值
bint                    %回归系数置信区间
stats                   %检验回归系统的统计量：复判定系数等
rcoplot(r, rint)  %残差向量与残差置信区间
%--根据rcoplot的绘制结果，剔除异常点之后重新生成回归系统--%

偏最小二乘回归（PLS） python代码

import numpy as np
x1 = [191, 189, 193, 162, 189, 182, 211, 167, 176, 154, 169, 166, 154, 247, 193, 202, 176, 157, 156, 138]
x2 = [36, 37, 38, 35, 35, 36, 38, 34, 31, 33, 34, 33, 34, 46, 36, 37, 37, 32, 33, 33]
x3 = [50, 52, 58, 62, 46, 56, 56, 60, 74, 56, 50, 52, 64, 50, 46, 62, 54, 52, 54, 68]
y1 = [5, 2, 12, 12, 13, 4, 8, 6, 15, 17, 17, 13, 14, 1, 6, 12, 4, 11, 15, 2]
y2 = [162, 110, 101, 105, 155, 101, 101, 125, 200, 251, 120, 210, 215, 50, 70, 210, 60, 230, 225, 110]
y3 = [60, 60, 101, 37, 58, 42, 38, 40, 40, 250, 38, 115, 105, 50, 31, 120, 25, 80, 73, 43]
# -----数据读取
data_raw = np.array([x1, x2, x3, y1, y2, y3])
data_raw = data_raw.T  # 输入原始数据，行数为样本数，列数为特征数
# -----数据标准化
num = np.size(data_raw, 0)  # 样本个数
mu = np.mean(data_raw, axis=0)  # 按列求均值
sig = (np.std(data_raw, axis=0))  # 按列求标准差
data = (data_raw - mu) / sig  # 标准化，按列减去均值除以标准差
# -----提取自变量和因变量数据
n = 3  # 自变量个数
m = 3  # 因变量个数
x0 = data_raw[:, 0:n]  # 原始的自变量数据
y0 = data_raw[:, n:n + m]  # 原始的变量数据
e0 = data[:, 0:n]  # 标准化后的自变量数据
f0 = data[:, n:n + m]  # 标准化后的因变量数据
# -----相关矩阵初始化
chg = np.eye(n)  # w到w*变换矩阵的初始化
w = np.empty((n, 0))  # 初始化投影轴矩阵
w_star = np.empty((n, 0))  # w*矩阵初始化
t = np.empty((num, 0))  # 得分矩阵初始化
ss = np.empty(0)  # 或者ss=[]，误差平方和初始化
press = []  # 预测误差平方和初始化
Q_h2 = np.zeros(n)  # 有效性判断条件值初始化
# -----求解主成分
for i in range(n):  # 主成分的总个数小于等于自变量个数
    # -----求解自变量的最大投影w和第一主成分t
    matrix = e0.T @ f0 @ f0.T @ e0  # 构造矩阵E'FF'E
    val, vec = np.linalg.eig(matrix)  # 计算特征值和特征向量
    index = np.argsort(val)[::-1]  # 获取特征值从大到小排序前的索引
    val_sort = val[index]  # 特征值由大到小排序
    vec_sort = vec[:, index]  # 特征向量按照特征值的顺序排列
    w = np.append(w, vec_sort[:, 0][:, np.newaxis], axis=1)  # 储存最大特征向量
    w_star = np.append(w_star, chg @ w[:, i][:, np.newaxis], axis=1)  # 计算 w*的取值
    t = np.append(t, e0 @ w[:, i][:, np.newaxis], axis=1)  # 计算投影
    alpha = e0.T @ t[:, i][:, np.newaxis] / (t[:, i] @ t[:, i])  # 计算自变量和主成分之间的回归系数
    chg = chg @ (np.eye(n) - (w[:, i][:, np.newaxis] @ alpha.T))  # 计算 w 到 w*的变换矩阵
    e1 = e0 - t[:, i][:, np.newaxis] @ alpha.T  # 计算残差矩阵
    e0 = e1  # 更新残差矩阵
    # -----求解误差平方和ss
    beta = np.linalg.pinv(t) @ f0  # 求回归方程的系数，数据标准化，没有常数项
    res = np.array(f0 - t @ beta)  # 求残差
    ss = np.append(ss, np.sum(res ** 2))  # 残差平方和
    # -----求解残差平方和press
    press_i = []  # 初始化误差平方和矩阵
    for j in range(num):
        t_inter = t[:, 0:i + 1]
        f_inter = f0
        t_inter_del = t_inter[j, :]  # 把舍去的第 j 个样本点保存起来,自变量
        f_inter_del = f_inter[j, :]  # 把舍去的第 j 个样本点保存起来，因变量
        t_inter = np.delete(t_inter, j, axis=0)  # 删除自变量第 j 个观测值
        f_inter = np.delete(f_inter, j, axis=0)  # 删除因变量第 j 个观测值
        t_inter = np.append(t_inter, np.ones((num - 1, 1)), axis=1)
        beta1 = np.linalg.pinv(t_inter) @ f_inter  # 求回归分析的系数,这里带有常数项
        res = f_inter_del - t_inter_del[:, np.newaxis].T @ beta1[0:len(beta1) - 1, :] - beta1[len(beta1) - 1, :]  # 计算残差
        res = np.array(res)
        press_i.append(np.sum(res ** 2))  # 残差平方和，并存储
    press.append(np.sum(press_i))  # 预测误差平方和
    # -----交叉有效性检验，判断主成分是否满足条件
    Q_h2[0] = 1
    if i > 0:
        Q_h2[i] = 1 - press[i] / ss[i - 1]
    if Q_h2[i] < 0.0975:
        print('提出的成分个数 r=', i + 1)
        break
# -----根据主成分t计算回归方程的系数
beta_Y_t = np.linalg.pinv(t) @ f0  # 求Y*关于t的回归系数
beta_Y_X = w_star @ beta_Y_t  # 求Y*关于X*的回归系数
mu_x = mu[0:n]  # 提取自变量的均值
mu_y = mu[n:n + m]  # 提取因变量的均值
sig_x = sig[0:n]  # 提取自变量的标准差
sig_y = sig[n:n + m]  # 提取因变量的标准差
ch0 = mu_y - mu_x[:, np.newaxis].T / sig_x[:, np.newaxis].T @ beta_Y_X * sig_y[:, np.newaxis].T  # 算原始数据回归方程的常数项
beta_target = np.empty((n, 0))  # 回归方程的系数矩阵初始化
for i in range(m):
    a = beta_Y_X[:, i][:, np.newaxis] / sig_x[:, np.newaxis] * sig_y[i]  # 计算原始数据回归方程的系数
    beta_target = np.append(beta_target, a, axis=1)
target = np.concatenate([ch0, beta_target], axis=0)  # 回归方程的系数，每一列是一个方程，每一列的第一个数是常数项
print(target)

程序结果为：

提出的成分个数 r= 2
[[ 4.70197312e+01 6.12567103e+02 1.83984900e+02]
[-1.66507920e-02 -3.50879763e-01 -1.25347701e-01]
[-8.23702347e-01 -1.02476743e+01 -2.49692623e+00]
[-9.69133092e-02 -7.41217596e-01 -5.18112643e-02]]

3、时间序列分析

①自适应滤波法

%% 自适应滤波法
clc, clear
yt = 0.1:0.1:1;
m = length(yt);
k = 0.9;          % 学习常数
N = 2;            % 权数个数
Terr = 10000;
w = ones(1,N) / N;
while abs(Terr)>0.00001
    Terr = [];
    for j = N+1:m-1
        yhat(j) = w*yt(j-1:-1:j-N)';
        err = yt(j) - yhat(j);
        Terr = [Terr, abs(Terr)];
        w = w + 2*k*err*yt(j-1:-1:j-N);
    end
    Terr = max(Terr);
end

②指数平滑法

二次指数平滑法

%% 二次指数平滑法
clc, clear
yt = [676 825 774 716 940 1159 1384 1524 1668 1688 1958 2031 2234 2566 2820 3006 3093 3277 3514 3770 4107]';
n = length(yt);
alpha = 0.3;
st1(1) = yt(1); st2(1) = yt(1);  % 初始值选实际初始值
for i = 2:n
    st1(i) = alpha*yt(i) + (1-alpha)*st1(i-1);
    st2(i) = alpha*st1(i) + (1-alpha)*st2(i-1);
end
at = 2*st1 - st2;
bt = alpha/(1-alpha)*(st1-st2);
yhat = at + bt;
y_predict = alpha*yt(n) + (1-alpha)*yhat(n);
x = 1965:1985;
plot(x, yt, '*', x, yhat);

③移动平均法

1、加权平均移动法

%% 加权移动平均法
clc ,clear
y = [6.35 6.20 6.22 6.66 7.15 7.89 8.72 8.94 9.28 9.80];
w = [1/6; 2/6; 3/6];   % 各加权项的权重
m = length(y);
n = 3;                 % 移动平均的项数
for i = 1:m-n+1
    yhat(i) = y(i:i+n-1)*w;
end
err = abs(y(n+1:m)-yhat(1:end-1))./y(n+1:m);  % 计算相对误差(最开始的三项数据是没有相对误差的)
T_err = 1 - sum(yhat(1:end-1))/sum(y(n+1:m)); % 计算总的相对误差
y_predict = yhat(end) / (1-T_err);            % 用总的相对误差修正预测值

2、趋势移动平均法

%% 趋势移动平均法
% 在一次移动平均的基础上再做一次移动平均
clc, clear
y = [676 825 774 716 940 1159 1384 1524 1668 1688 1958 2031 2234 2566 2820 3006 3093 3277 3514 3770 4107];
% 第一次移动平均
m1 = length(y);
n = 6;    % 移动平均的项数
for i = 1:m1-n+1
    yhat1(i) = sum(y(i:i+n-1))/n;
end
% 第二次移动平均
m2 = length(yhat1);
for i = 1:m2-n+1
    yhat2(i) = sum(yhat1(i:i+n-1))/n;
end
plot(1:m1, y, '*');
% 计算平滑系数
at = 2*yhat1(end) - yhat2(end);
bt = 2*(yhat1(end)-yhat2(end)) / (n-1);
% 预测后两个数值
y_predict1 = at + bt;
y_predict2 = at + 2*bt;

3、简单移动平均法

%% 简单移动平均法
clc, clear
y = [533.8 574.6 606.9 649.8 705.1 772.0 816.4 892.7 963.9 1015.1 1102.7];
m = length(y);
n = [4,5];    % n位移动平均的项数，选取4和5分别做一次运算
for i = 1:length(n)
    for j = 1:m-n(i)+1
        yhat{i}(j) = sum(y(j:j+n(i)-1))/n(i);
    end
    y_predict(i) = yhat{i}(end);  % 预测值
    s(i) = sqrt(mean( (y(n(i)+1:m) - yhat{i}(1:end-1)).^2 )); % 预测的标准误差
end

4、微分方程

参考之前的文章：《MATLAB--微分方程》

http://t.csdn.cn/ub34W

二、长期预测

1、神经网络预测

参考之前的文章：

http://t.csdn.cn/zw7ou

以及参考深度学习专栏

搭建神经网络进行一些模型的预测

2、logistic模型

①模型介绍

优点：计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。
使用数据类型：数值型和标称型数据。

②模型分析及代码

荷兰生物学家 Verhaust 于 1838 年提出了以昆虫数量为基础的 Logistic 人口增长模型。这个模型假设增长率 r 是人口的函数，它随着 x 的增加而减少。由 r(x)的表达式可知，当 x=𝑥𝑚时， r=0。其中， 𝑥𝑚表示自然资源条件能容纳的最大人口数。 Logistic 模型综合考虑了环境等因素对人口增长产生的影响，因此也是一种被广泛应用的效果较好的模型。\n\n设时刻 t 时人口为 x(t)，环境允许的最大人口数量为𝑥𝑚，人口净增长率随人口数量的增加而线性减少，即：

体现了环境和资源对人口增长的阻滞作用，显然 x 越大，该因子越大，说明随着人口数量 x 的增加，阻滞作用越来越大。\n\n由此建立 Logistic 人口模型的微分方程:

根据附件给出的 1997-2016 年每年的人口数量，运用 MATLAB 进行编程处理，可以比较 1997-2016 年实际人口与拟合线的拟合程度，由图 1.1 可见， Logistic 模型对过去 20 年人口数量拟合效果较好。通过拟合，得到了待求参数 r=0.0394， 𝑥𝑚=1.5501× 105。因为以 1997 年为起算点，所以𝑥0=1.23626× 105。则 Logistic 人口模型函数方程为:

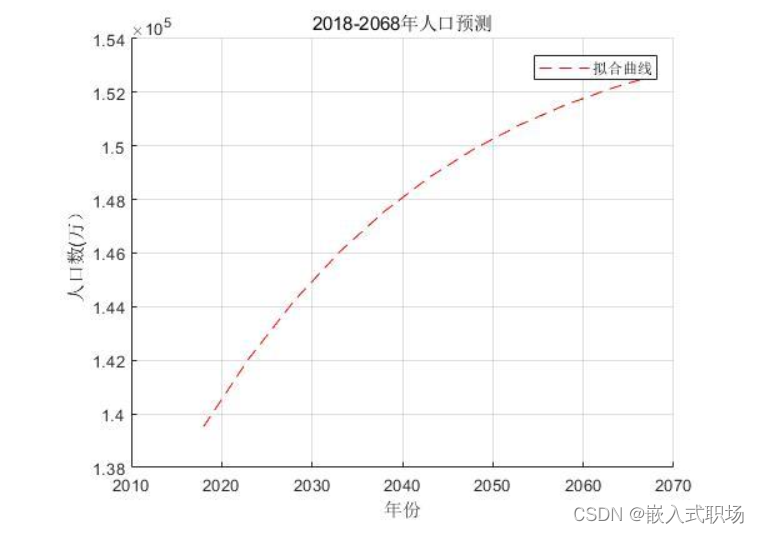
由 MATLAB 拟合出来的 Logistic 函数进行 2018-2068 年的人口预测，人口数缓慢上升，经过 50 年人口增长了 13120 万人， Logistic 模型也求得在资源和环境的限制下，无论过了多少年的人口不会超过 155010万人。在考虑资源和环境的阻滞作用随着人口增多也会越来越大的情况下，上述结果与实际是相符合的。

clc,clear,
t=1997:1:2016;
x=[123626 124761 125786 126743 127627 128453 129227 129988 130756 131448
132129 132802 133450 134091 134735 135404 136072 136782 137462 138271];
x1=[123626 124761 125786 126743 127627 128453 129227 129988 130756 131448
132129 132802 133450 134091 134735 135404 136072 136782 137462];
x2=[124761 125786 126743 127627 128453 129227 129988 130756 131448 132129
132802 133450 134091 134735 135404 136072 136782 137462 138271];
dx=(x2-x1)./x2;a=polyfit(x2,dx,1);
r=a(2),xm=-r/a(1)
x0=123626;
f=inline('xm./(1+(xm/x0-1)*exp(-r*(t-1997)))','t','xm','r','x0');
scatter(t,x,'k');
hold on;
plot(t,f(t,xm,r,x0),'r-');
xlabel('年份');
ylabel('人口数(万） ');
title('1997-2016 年实际人口与拟合值比较');
grid on;
x2017=f(2017,xm,r,x0),x2018=f(2018,xm,r,x0),x2023=f(2023,xm,r,x0)
x2028=f(2028,xm,r,x0),x2033=f(2033,xm,r,x0),x2038=f(2038,xm,r,x0)
x2043=f(2043,xm,r,x0),x2048=f(2048,xm,r,x0),x2053=f(2053,xm,r,x0)
x2058=f(2058,xm,r,x0),x2063=f(2063,xm,r,x0),x2068=f(2068,xm,r,x0)
z=2018:5:2068;y=[x2018,x2023,x2028,x2033,x2038,x2043,x2048,x2053,x2058,x206
3,x2068];
hold on;
plot(z,y,'--r');xlabel('年份');ylabel('人口数(万） ');title('曲线拟合以及人口
预测曲线')
grid on;

clc,clear
num=xlsread('C:\Users\\Desktop\Book1.xlsx','sheet1','B2:B21');
x1=num;
for i=1:18
m1(i+2)=(x1(i)+x1(i+1)+x1(i+2))/3;
end
for i=3:18
m2(i+2)=(m1(i)+m1(i+1)+m1(i+2))/3;
end
m1=m1';
m2=m2';
a=2*m1-m2;
b=m1-m2;
for i=1:52
y(:,i)=a(20,1)+b(20,1)*i;
end
y
figure;
x=1:1:52;
plot(x,y,'--r');
xlabel('年份');
ylabel('预测值');
legend('预测值');
title('2018-2068 年人口预测')

文章应用案例来自：http://t.csdn.cn/9cmBB

标签： python matlab 数据分析

本文转载自: https://blog.csdn.net/m0_58585940/article/details/127720448
版权归原作者 派大星先生c 所有，如有侵权，请联系我们删除。

数学建模--预测类模型

一、中短期预测

1、灰色预测法

①适用范围

②模型实现

2、回归分析

①适用范围

②模型实现

3、时间序列分析

①自适应滤波法

②指数平滑法

③移动平均法

4、微分方程

二、长期预测

1、神经网络预测

2、logistic模型

①模型介绍

②模型分析及代码

发表评论

“数学建模--预测类模型”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航