在不平衡数据上训练的分类算法往往导致预测质量差。模型严重偏向多数类,忽略了对许多用例至关重要的少数例子。这使得模型对于涉及罕见但高优先级事件的现实问题来说不切实际。
过采样提供了一种在模型训练开始之前重新平衡类的方法。通过复制少数类数据点,过采样平衡了训练数据,防止算法忽略重要但数量少的类。虽然存在过拟合风险,但过采样可以抵消不平衡学习的负面影响,可以让机器学习模型获得解决关键用例的能力
常见的过采样技术包括随机过采样、SMOTE(合成少数过采样技术)和ADASYN(不平衡学习的自适应合成采样方法)。随机过采样简单地复制少数样本,而SMOTE和ADASYN策略性地生成合成的新数据来增强真实样本。
什么是过采样
过采样是一种数据增强技术,用于解决类不平衡问题(其中一个类的数量明显超过其他类)。它旨在通过扩大属于代表性不足的类别的样本量来重新平衡训练数据分布。
过采样通过复制现有样本或生成合成的新数据点来增加少数类样本。这是通过复制真实的少数观察结果或根据真实世界的模式创建人工添加来实现的。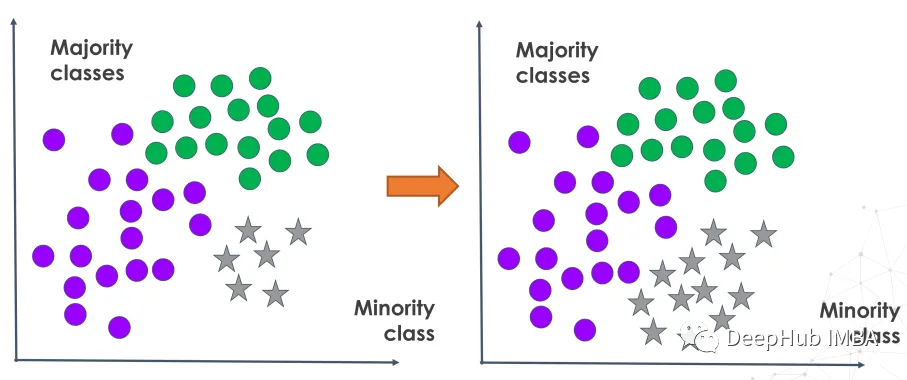
在模型训练之前通过过采样放大代表性不足的类别,这样模型学习可以更全面地代表所有类别,而不是严重倾向于占主导地位的类别。这改进了用于解决涉及检测重要但不常见事件的需求的各种评估度量。
为什么要过采样
当处理不平衡数据集时,我们通常对正确分类少数类感兴趣。假阴性(即未能检测到少数类别)的成本远高于假阳性(即错误地将样本识别为属于少数类别)的成本。
传统的机器学习算法,如逻辑回归和随机森林目标优化假设均衡类分布的广义性能指标。所以在倾斜数据上训练的模型往往非常倾向于数量多的类,而忽略了数量少但重要的类的模式。
通过对少数类样本进行过采样,数据集被重新平衡,以反映所有结果中更平等的错误分类成本。这确保了分类器可以更准确地识别代表性不足的类别,并减少代价高昂的假阴性。
过采样VS欠采样
过采样和欠采样都是通过平衡训练数据分布来解决类不平衡的技术。他们以相反的方式达到这种平衡。
过采样通过复制或生成新样本来增加少数类来解决不平衡问题。而欠采样通过减少代表性过高的多数类别中的样本数量来平衡类别。
当大多数类有许多冗余或相似的样本或处理庞大的数据集时,就可以使用欠采样。但是它欠采样有可能导致信息的丢失,从而导致有偏见的模型。
当数据集很小并且少数类的可用样本有限时,就可以使用过采样。由于数据重复或创建了不代表真实数据的合成数据,它也可能导致过拟合。
下面我们将探讨不同类型的过采样方法。
1、随机过采样
随机过采样随机复制少数类样本以平衡类分布,所以他的实现非常简单。它以随机的方式从代表性不足的类别中选择现有的样本,并在不改变的情况下复制它们。这样做的好处是当数据集规模较小时,可以有效地提高少数观测值,而不需要收集额外的真实世界数据。
imbalanced-learn 库中的randomoverampler可以实现过采样的过程。
from imblearn.over_sampling import RandomOverSampler
from imblearn.pipeline import make_pipeline
X, y = create_dataset(n_samples=100, weights=(0.05, 0.25, 0.7))
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(15, 7))
clf.fit(X, y)
plot_decision_function(X, y, clf, axs[0], title="Without resampling")
sampler = RandomOverSampler(random_state=0)
model = make_pipeline(sampler, clf).fit(X, y)
plot_decision_function(X, y, model, axs[1],
f"Using {model[0].__class__.__name__}")
fig.suptitle(f"Decision function of {clf.__class__.__name__}")
fig.tight_layout()
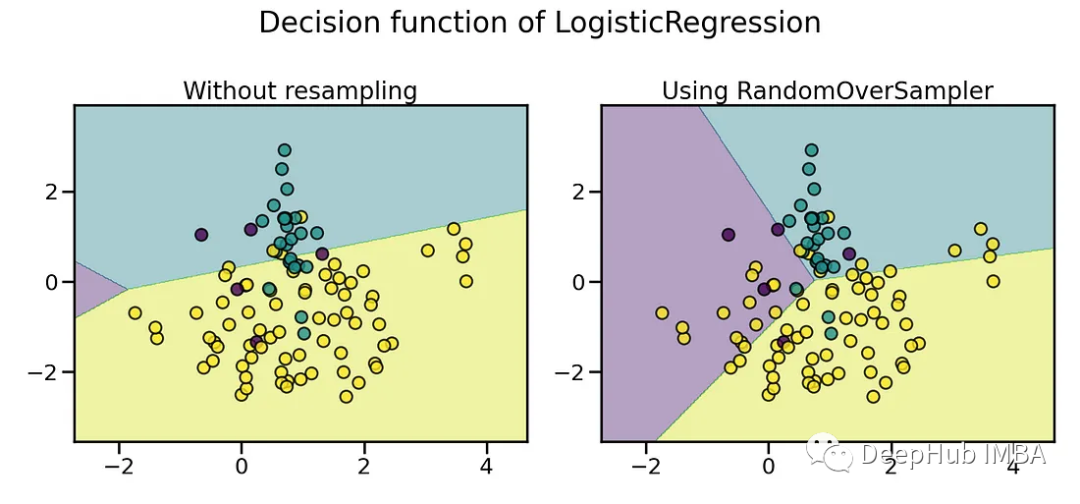
上图可以看到,通过复制样本,使得少数类的在分类结果中被正确的识别了。
2、平滑的自举过采样
带噪声的随机过采样是简单随机过采样的改进版本,目的是解决其过拟合问题。这种方法不是精确地复制少数类样本,而是通过将随机性或噪声引入现有样本中来合成新的数据点。
默认情况下,随机过采样会产生自举。收缩参数则在生成的数据中添加一个小的扰动来生成平滑的自举。下图显示了两种数据生成策略之间的差异。
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(15, 7))
sampler.set_params(shrinkage=1)
plot_resampling(X, y, sampler, ax=axs[0], title="Normal bootstrap")
sampler.set_params(shrinkage=0.3)
plot_resampling(X, y, sampler, ax=axs[1], title="Smoothed bootstrap")
fig.suptitle(f"Resampling with {sampler.__class__.__name__}")
fig.tight_layout()
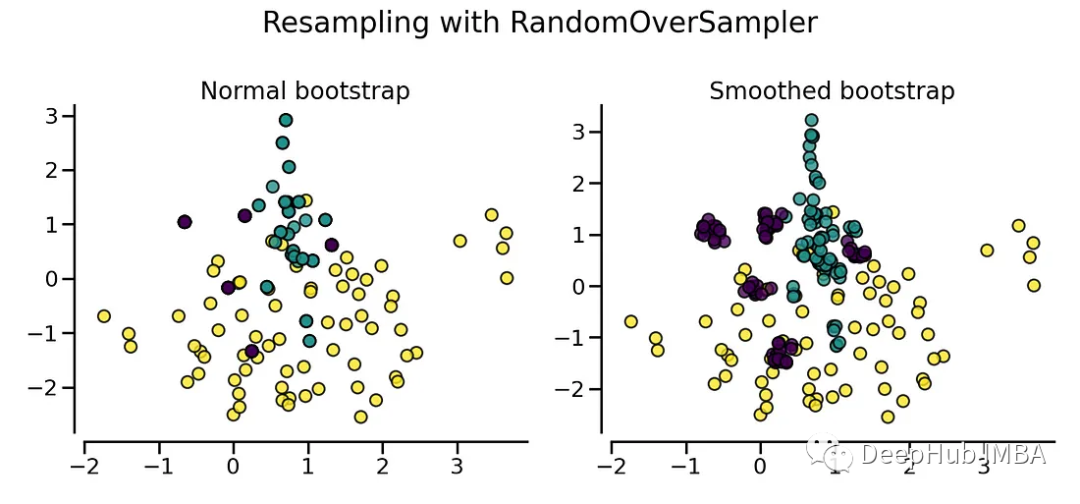
平滑的自举插值不是任意重复少数观察样本,而是创建新的数据点,这些数据点是来自真实样本的特征向量的组合或插值。这样做的效果是,通过数据扩展而不是直接复制,将可用的少数数据扩展到原始记录之外。
插值的数据点是“平滑”的组合,它们占据真实样本周围的特征空间,而不是覆盖在它们上面。因此与随机过采样相比,平滑自举过采样产生了更多新的合成少数样本。这有助于解决来自重复技术的过拟合问题,同时仍然平衡类分布。
随机过采样的好处是它是一种非常直接和简单的技术。它不需要复杂的算法或对数据底层分布的假设。因此,它可以很容易地应用于任何不平衡的数据集,而不需要特殊的先验知识。
但是随机过采样也受到过拟合可能性的限制。由于它只是复制了现有的少数样本的例子,而不是产生真正的新样本,所以观察结果并没有提供关于代表性不足的类的额外信息细节。而且这种重复也有可能放大了训练数据中的噪声,而不是更全面地正确表征少数类。
这样训练出来的模型模型可能会过度定制初始数据集的特定细微差别,而不是捕获真正的底层模式。这就限制了它们在面对新的未知数据时的泛化能力。
3、SMOTE
SMOTE(Synthetic Minority Oversampling Technique)是一种广泛应用于机器学习中缓解类失衡问题的过采样方法。
SMOTE背后的关键概念是,它通过插值而不是复制,为代表性不足的类生成新的合成数据点。它随机选择一个少数类观测值,并根据特征空间距离确定其最近的k个相邻少数类样本。
然后通过在初始样本和k个邻居之间进行插值生成新的合成样本。这种插值策略合成了新的数据点,这些数据点填充了真实观测之间的区域,在功能上扩展了可用的少数样本,而不需要复制原始记录。
SMOTE 的工作流程如下:
- 对于每个少数类样本,计算其在特征空间中的 K 近邻样本,K 是一个用户定义的参数。
- 针对每个少数类样本,从其 K 近邻中随机选择一个样本。
- 对于选定的近邻样本和当前少数类样本,计算它们之间的差异,并乘以一个随机数(通常在 [0, 1] 之间),将该乘积加到当前样本上,生成新的合成样本。
- 重复上述步骤,为每个少数类样本生成一定数量的合成样本。
- 将生成的合成样本与原始数据合并,用于训练分类模型。
SMOTE 的关键优势在于通过合成样本能够增加数据集中少数类的样本数量,而不是简单地重复已有的样本。这有助于防止模型对于过拟合少数类样本,同时提高对未见过样本的泛化性能。
SMOTE 也有一些变种,例如 Borderline-SMOTE 和 ADASYN,它们在生成合成样本时考虑了样本的边界情况和密度信息,进一步改进了类别不平衡问题的处理效果。
4、自适应合成采样(ADASYN)
自适应合成采样(Adaptive Synthetic Sampling,ADASYN) 是一种基于数据重采样的方法,它通过在特征空间中对少数类样本进行合成生成新的样本,从而平衡不同类别的样本分布。与简单的过采样方法(如重复少数类样本)不同,ADASYN 能够根据样本的密度分布自适应地生成新的样本,更注重在密度较低的区域生成样本,以提高模型对边界区域的泛化能力。
ADASYN 的工作流程如下:
- 对于每个少数类样本,计算其在特征空间中的 K 近邻样本,K 是一个用户定义的参数。
- 计算每个少数类样本与其 K 近邻样本之间的样本密度比,该比例用于表示样本所在区域的密度。
- 对于每个少数类样本,根据其样本密度比,生成一定数量的合成样本,使得合成样本更集中在密度较低的区域。
- 将生成的合成样本与原始数据合并,用于训练分类模型。
ADASYN 的主要目标是在增加少数类样本的同时,尽量保持分类器在决策边界附近的性能。也就是说如果少数类的一些最近邻来自相反的类,来自相反类的邻居越多,它就越有可能被用作模板。在选择模板之后,它通过在模板和同一类的最近邻居之间进行插值来生成样本。
生成方法对比
from imblearn import FunctionSampler # to use a idendity sampler
from imblearn.over_sampling import ADASYN, SMOTE
X, y = create_dataset(n_samples=150, weights=(0.1, 0.2, 0.7))
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))
samplers = [
FunctionSampler(),
RandomOverSampler(random_state=0),
SMOTE(random_state=0),
ADASYN(random_state=0),
]
for ax, sampler in zip(axs.ravel(), samplers):
title = "Original dataset" if isinstance(sampler, FunctionSampler) else None
plot_resampling(X, y, sampler, ax, title=title)
fig.tight_layout()
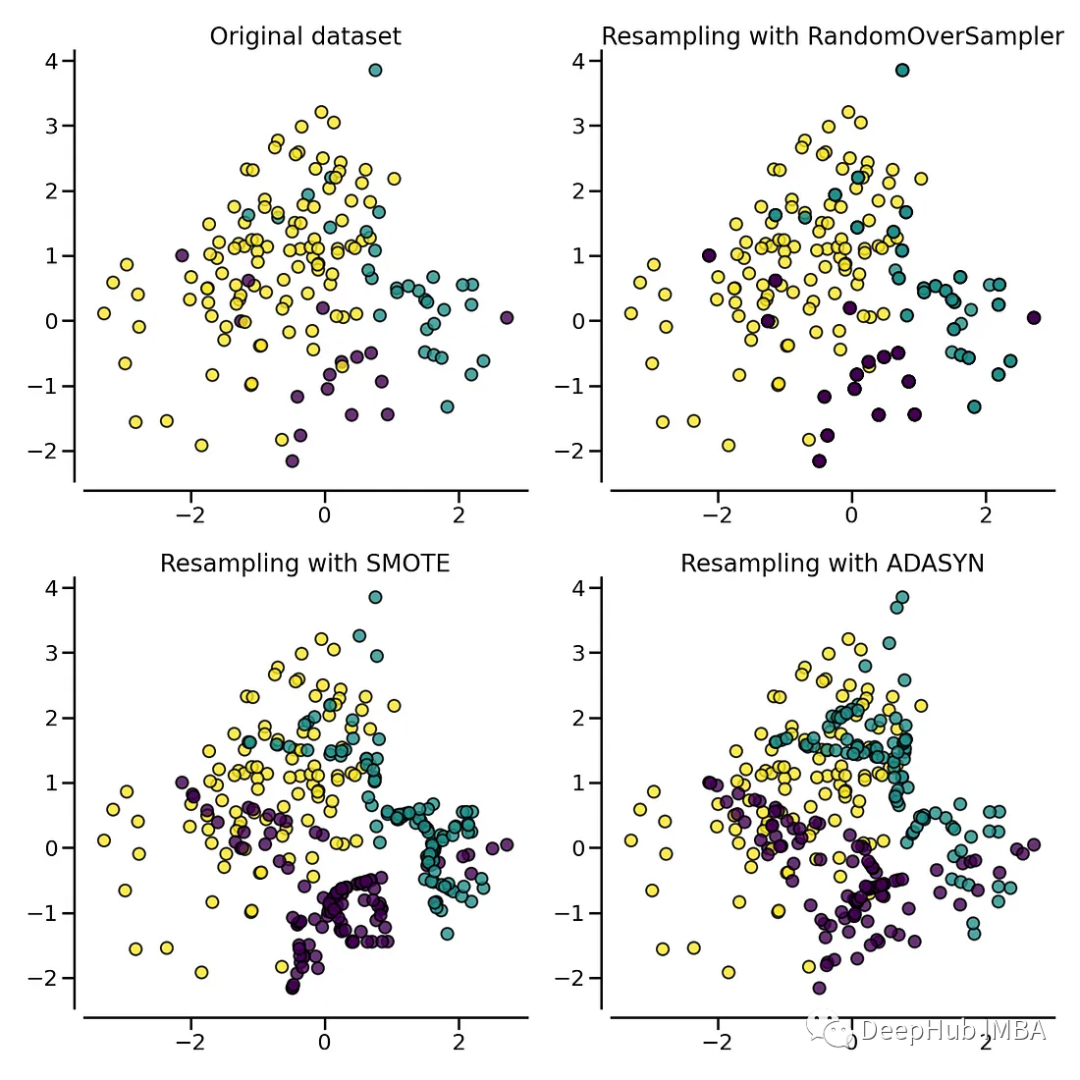
上图可以看到ADASYN和SMOTE之间的区别。ADASYN将专注于难以分类的样本,而常规SMOTE将不做任何区分。
下面我们看看不同算法的分类结果
X, y = create_dataset(n_samples=150, weights=(0.05, 0.25, 0.7))
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(20, 6))
models = {
"Without sampler": clf,
"ADASYN sampler": make_pipeline(ADASYN(random_state=0), clf),
"SMOTE sampler": make_pipeline(SMOTE(random_state=0), clf),
}
for ax, (title, model) in zip(axs, models.items()):
model.fit(X, y)
plot_decision_function(X, y, model, ax=ax, title=title)
fig.suptitle(f"Decision function using a {clf.__class__.__name__}")
fig.tight_layout()
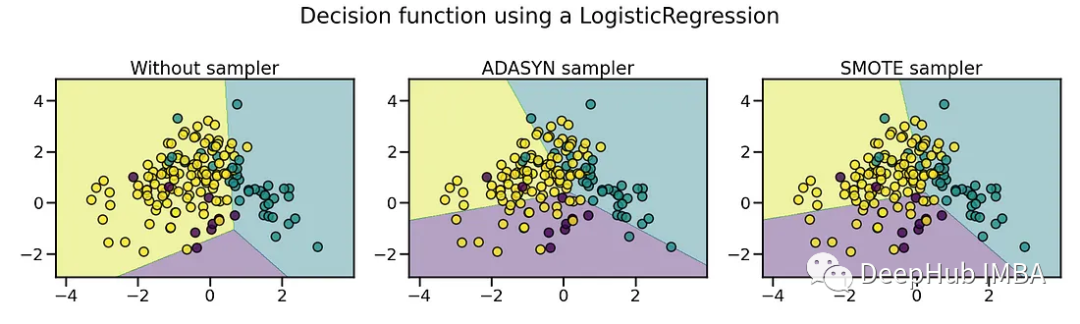
可以看到如果不进行过采样,那么少数类基本上没法区分。通过过采样的技术,少数类得到了有效的区分。
SMOTE对所有的少数类样本平等对待,不考虑它们之间的分布密度。ADASYN考虑到每个少数类样本的邻近样本数量,使得对于那些邻近样本较少的少数类样本,生成更多的合成样本,以便更好地覆盖整个决策边界。
但是这两个算法还要根据实际应用时选择,比如上图中黄色和蓝色的决策边界变化的影响需要实际测算后才能判断那个算法更适合当前的应用。
作者:Abdallah Ashraf