1 Ornstein-Uhlenbeck过程
用SDE的形式表示，Ornstein-Uhlenbeck过程为：
- θ就是均值回归的速率（θ越大，干扰越小）
- μ是均值
- σ是波动率（扰动的程度）
- ε ~N(0,1)
从SDE的角度看，随机过程包含两块：
- 第一部分表示均值回归，即不论如何变化，下一时刻总会朝着均值方向变化
- 第二部分就是一个布朗运动生成的随机项
1.1 解析解推导
定义
,根据伊藤引理，有：
数学知识整理：布朗运动与伊藤引理 （Ito‘s lemma）_UQI-LIUWJ的博客-CSDN博客
![=(\theta X_t e^{\theta t}+[\theta(\mu-X_t)]e^{\theta t}+\frac{1}{2}\sigma^2 \cdot 0)dt+e^{\theta t} \sigma \epsilon \sqrt{dt}](https://latex.codecogs.com/gif.latex?%3D%28%5Ctheta%20X_t%20e%5E%7B%5Ctheta%20t%7D+%5B%5Ctheta%28%5Cmu-X_t%29%5De%5E%7B%5Ctheta%20t%7D+%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2%20%5Ccdot%200%29dt+e%5E%7B%5Ctheta%20t%7D%20%5Csigma%20%5Cepsilon%20%5Csqrt%7Bdt%7D) 
然后我们计算
 将
移到等号右边去，同时等号左右同时除以
(
的系数）
有：
又根据伊藤等距，有：数学知识整理：布朗运动与伊藤引理 （Ito‘s lemma）_UQI-LIUWJ的博客-CSDN博客
然后因为
，所以
1.2 离散解
如果我们考虑离散形式，记单步step为τ：
形式上就是 ，也即自回归形式AR(1)
1.2.1 离散解在RL中的延申
通过上一小段，不难发现Ornstein-Uhlenbeck过程是时序相关的【且满足马尔科夫性，后一步的噪声仅受前一步的影响】，所以在强化学习的前一步和后一步的动作选取过程中可以**利用Ornstein-Uhlenbeck过程产生时序相关的噪声**，以提高在惯性系统（环境）中的控制任务的探索效率。【上一步的噪声和下一步的噪声之间是有单步自回归的关系）
常用的高斯噪声是时序上不相关的，前一步和后一步选取动作的时候噪声都是独立的。
——>相比于独立噪声，**OU噪声适合于惯性系统，尤其是时间离散化粒度较小的情况 **(时间离散化粒度大的时候，可能OU噪声和高斯噪声的区别就不明显了）
——>在惯性系统中，如果使用高斯噪声，那么会产生一系列独立的在0均值附近的高斯噪声，原地震荡，使得随机噪声的作用被平均/抵消了
——>如果使用OU噪声的话，会顺着惯性往一个方向多探索几步，这样可以累计探索的效果
2 代码实现
import numpy as np
import matplotlib.pyplot as plt
class Ornstein_Uhlenbeck_Noise:
def __init__(self, mu, sigma=1.0, theta=0.15, dt=1e-2, x0=None):
self.theta = theta
self.mu = mu
self.sigma = sigma
self.dt = dt
self.x0 = x0
self.reset()
def __call__(self):
x = self.x_prev + \
self.theta * (self.mu - self.x_prev) * self.dt + \
self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)
'''
后两行是dXt，其中后两行的前一行是θ(μ-Xt)dt，后一行是σεsqrt(dt)
'''
self.x_prev = x
return x
def reset(self):
if self.x0 is not None:
self.x_prev = self.x0
else:
self.x_prev = np.zeros_like(self.mu)
2.1 和高斯噪声的比较
ou_noise = Ornstein_Uhlenbeck_Noise(mu=np.zeros(1))
y1 = []
y2 = np.random.normal(0, 1, 1000) #高斯噪声
for _ in range(1000):
y1.append(ou_noise())
fig,ax=plt.subplots(1,2,figsize=(10,5))
ax[0].plot(y1, c='r')
ax[0].set_title('OU noise')
ax[1].plot(y2, c='b')
ax[1].set_title('Guassian noise')
plt.show()
可以看到OU噪声是一个有一定自回归的噪声，而高斯噪声是两两独立的
OU noise往往不会高斯噪声一样相邻的两步的值差别那么大，而是会绕着均值依据惯性在上一步附近正向或负向探索一段距离，就像物价和利率的波动一样，这有利于在一个方向上探索。
2.2 不同参数的影响
2.2.1 sigma
if __name__ == "__main__":
ou_noise1 = Ornstein_Uhlenbeck_Noise(sigma=1,mu=np.zeros(1))
ou_noise2 = Ornstein_Uhlenbeck_Noise(sigma=0.1,mu=np.zeros(1))
y1 = []
y2 = []
for _ in range(1000):
y1.append(ou_noise1())
y2.append(ou_noise2())
fig,ax=plt.subplots(1,2,figsize=(10,5))
ax[0].plot(y1, c='r')
ax[0].set_title('OU noise_sigma=1')
ax[1].plot(y2, c='b')
ax[1].set_title('OU noise_sigma=0.1')
plt.show()
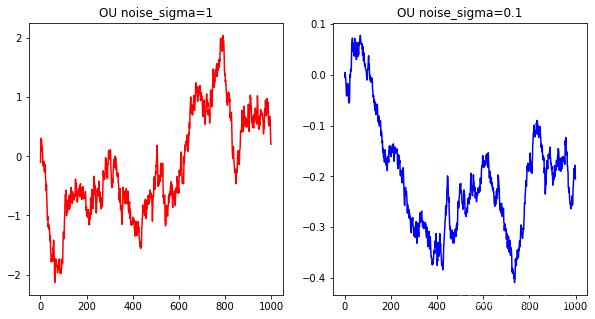
σ大，那么扰动就会大一些
2.2.2 dt
if __name__ == "__main__":
ou_noise1 = Ornstein_Uhlenbeck_Noise(dt=1e-2,mu=np.zeros(1))
ou_noise2 = Ornstein_Uhlenbeck_Noise(dt=1,mu=np.zeros(1))
y1 = []
y2 = []
for _ in range(1000):
y1.append(ou_noise1())
y2.append(ou_noise2())
fig,ax=plt.subplots(1,2,figsize=(10,5))
ax[0].plot(y1, c='r')
ax[0].set_title('OU noise_dt=1e-2')
ax[1].plot(y2, c='b')
ax[1].set_title('OU noise_dt=1')
plt.show()
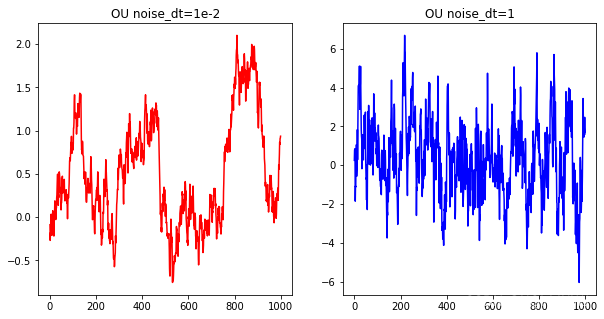
这也印证了前面1.2.1的说法：时间离散化粒度大的时候，可能OU噪声和高斯噪声的区别就不明显了【这可能是很多地方说OU噪声没有作用的一个原因。。。】
2.2.3 theta
if __name__ == "__main__":
ou_noise1 = Ornstein_Uhlenbeck_Noise(theta=0.15,mu=np.zeros(1))
ou_noise2 = Ornstein_Uhlenbeck_Noise(theta=1,mu=np.zeros(1))
y1 = []
y2 = []
for _ in range(1000):
y1.append(ou_noise1())
y2.append(ou_noise2())
fig,ax=plt.subplots(1,2,figsize=(10,5))
ax[0].plot(y1, c='r')
ax[0].set_title('OU noise_theta=0.15')
ax[1].plot(y2, c='b')
ax[1].set_title('OU noise_theta=1')
plt.show()
θ大，那么向均值考虑的程度就会更猛烈一些
参考内容
强化学习中Ornstein-Uhlenbeck噪声是鸡肋吗？ - 知乎 (zhihu.com)
本文转载自: https://blog.csdn.net/qq_40206371/article/details/125713187
版权归原作者 UQI-LIUWJ 所有， 如有侵权，请联系我们删除。
版权归原作者 UQI-LIUWJ 所有， 如有侵权，请联系我们删除。