基于等效燃油消耗最小的并联式混合动力汽车实时优化能量管理策略研究

0 引言

   目前，混合动力汽车仍然是实现汽车节能减排的有效途径之一，而能量管理策略对发挥其节能减排的潜力有着至关重要的影响。当前能量管理策略主要分为两大类: 基于规则能量管理策略和基于最优化能量管理策略。基于优化的控制策略，如动态规划，DP、极小值原理，PMP、随机动态规划，SDP、模型预测控制，MPC、等效燃油消耗最小策略，ECMS等能取得最优的燃油经济性，其中 ECMS 是实时优化策略，最有可能进行实车应用，但计算复杂限制了其在实车中的应用。规则控制策略简单，能应用于实车，但规则制定主要依靠人的经验，控制效果不佳。为克服最优控制和规则控制的缺点，提出了很多有效的方法来优化基于规则的能量管理策略，如利用遗传算法、DP算法、结合基于规则与ECMS的能量管理策略，还有离线生成控制 MAP，通过在线插值实现实时控制。这些方法具有实时性，但是都存在一定的缺陷，因为基于一种或者几种特定工况提取的规则或MAP，鲁棒性不强，一般只是针对特定工况控制效果较好。

   因此，为实现 ECMS 策略实时控制，本项目中在ECMS 控制规律的定性分析基础上，提出几种近似ECMS 算法的自适应规则控制策略，实现与ECMS 策略近似的节油效果，且能克服 ECMS 实时性差的问题。

1 并联式混合动力汽车系统构型

1.1 动力系统结构及工作模式

   本项目研究的混合动力电动汽车为一单轴并联式混合动力汽车，其动力系统结构如图1 所示。该并联式 HEV 的动力总成系统主要包括发动机、电机、离合器、传动系及电池。其中，电机直接与离合器的输出和传动系的输入相连。电机转子同时作为转矩耦合器直接使用。因此，省略了机械耦合器，这种车辆动力总成系统结构简单紧凑。这种结构中，电机有发动机启动器、回馈制动中的发电机以及发动机辅助三个功能。这种车辆模型可以在发动机单独驱动、电机单独驱动、混合驱动和回馈制动四种模型下自由切换工作。

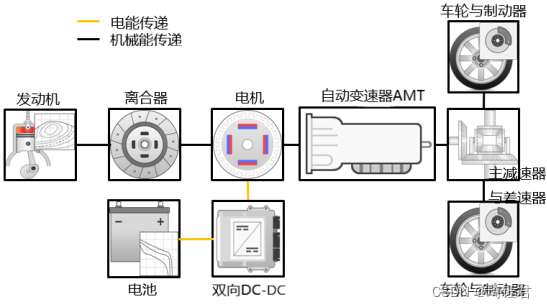
图1 并联式混合动力汽车动力总成系统结构图

1.2 车辆纵向动力学模型

** **车辆动力系统建模是理解车辆运行规律的第一步。选择能代表车辆动力学和动力系统关键部件特征的参数，准确反映车辆运行规律；同时，减少不必要的参数使用量，提高模型的运算时间。准确的HEV动力学模型可以提高能量管理算法的精度。由于能量管理策略设计与车辆纵向速度正相关，而与车辆其他方向的速度无关，本项目忽略了车辆的横向动力学特性和驾驶稳定性，仅根据车辆纵向动力学来对车辆运动进行建模。根据车辆行驶过程中的动力学平衡关系，作用在车轮上的转矩 $T_{w}$ 可表示为：

(1)

其中， $\rho _{a}$ 为空气密度； $m$ 为整车总质量； $f_{r}$ 为滚动阻力系数； $\upsilon$ 为车速； $C_{D}$ 为空气阻力系数； $A_{f}$ 为迎风面积； $\alpha$ 为道路坡道角； $\delta$ 为旋转质量换算系数； $R_{w}$ 为车轮半径。

   车轮转矩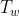![T_{w}](https://latex.codecogs.com/gif.latex?T_%7Bw%7D)和发动机转矩以及电机转矩之间的关系为：

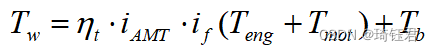
(2)

其中， $\eta _{t}$ 为传递效率； $i_{AMT}$ 为变速器传动比； $i_{f}$ 为主减速器传动比； $T_{eng}$ 为发动机转矩； $T_{mot}$ 为电机转矩； $T_{b}$ 为制动转矩。

1.3 发动机模型

    本项目发动机采用准静态模型，每个时刻下的油耗可通过查发动机的燃油消耗MAP得到：

(3)

其中， $\dot{m}_{fuel}$ 为燃油消耗率，可通过一定转速和转矩查找准静态发动机万有特性MAP图得到。图2为发动机燃油消耗率特性图。

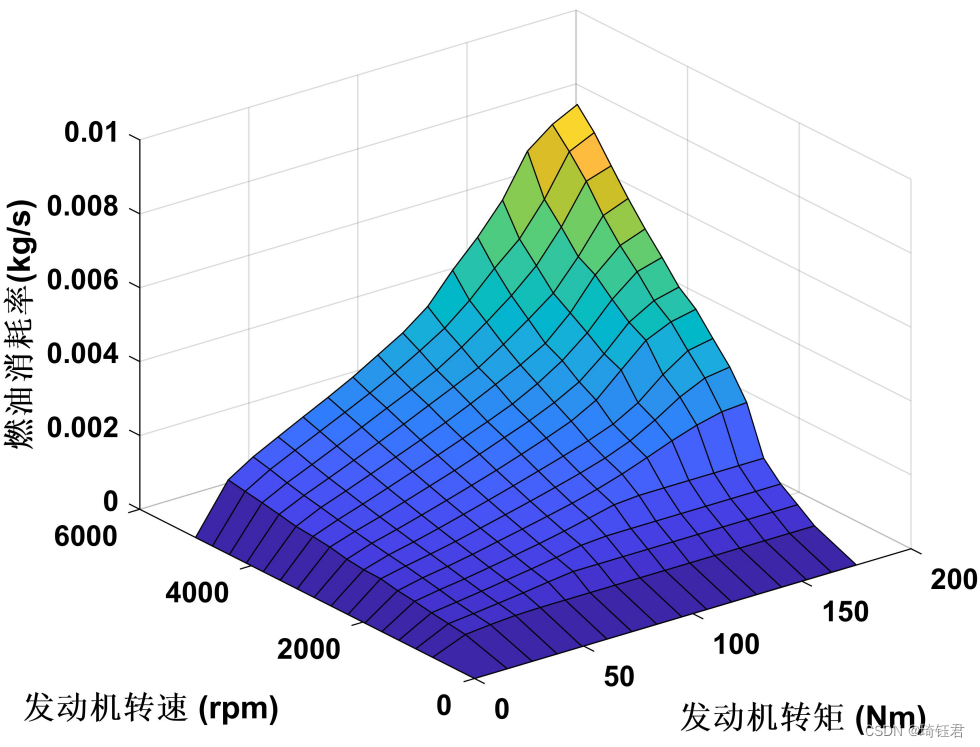
图2 发动机比油耗特性图

1.4 电机模型

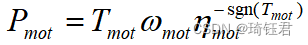
   电机选用永磁同步电机，在工作过程中既可作为牵引电机提供转矩，也可作为发电机给电池充电，因此电机的功率 ![P_{mot}](https://latex.codecogs.com/gif.latex?P_%7Bmot%7D)可表示为：

(4)

其中， $\eta _{mot}$ 为电机效率，可通过一定转速和转矩查找电机准静态效率MAP图得到。图3为电机效率特性图。

图3 电机效率特性图

1.5 电池模型

   忽略温度对电池的影响，采用Rint模型对电池建模，获得电池SOC和输出功率表达式为：

(5)

其中， $U_{oc}$ 为电池开路电压； $R_{int}$ 为电池内阻； $P_{batt}$ 为电池功率； $Q_{batt}$ 为电池最大容量。

2 基于等效燃油消耗最小的能量管理策略

2.1 能量管理最优问题描述

   以最佳燃油经济性为优化目标，性能泛函为：

(6)

其中， $u(t)$ 为控制变量； $\dot{m}_{fuel}$ 为瞬时燃油消耗率； $[t_{0},t_{f}]$ 为优化时域；针对单轴并联式HEV，其状态变量 $x(t)=SOC(t)$ ，控制变量 $u(t)=T_{eng}(t)$ 。

   约束条件为：

(7)

    上述最优控制问题的汉密尔顿函数为:

(8)

    ECMS 由极小值原理推导而来，其等效油耗![\dot{m}_{eqv}](https://latex.codecogs.com/gif.latex?%5Cdot%7Bm%7D_%7Beqv%7D)由实际油耗![\dot{m}_{fuel}](https://latex.codecogs.com/gif.latex?%5Cdot%7Bm%7D_%7Bfuel%7D)和与电能相对应的名义油耗![\dot{m}_{ess}](https://latex.codecogs.com/gif.latex?%5Cdot%7Bm%7D_%7Bess%7D)两部分构成，相应的瞬时消耗率亦然：

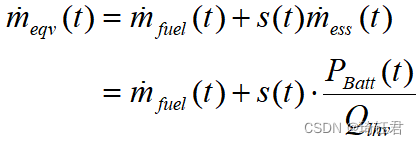
(10)

其中， $s(t)$ 为等效燃油消耗因子，简称等效因子； $Q_{lhv}$ 为燃油低热值。

   对比式(8)和式(10)可得到协调变量和等效因子之间的对应关系为：

(11)

2.2 等效因子计算

2.2.1 等效因子构建——方法一

   根据哈密顿-雅可比-贝尔曼方程，可以得到优化的协调变量：

(12)

  优化目标函数通常包含发动机燃油消耗和电机等效油耗，本文考虑维持电池SOC平衡，可将目标函数写为式：

(13)

其中， $SOC_{ref}$ 为参考SOC值， $\xi$ 为惩罚因子， $\bar{\eta}_{s(t)}=\bar{\eta }_{mot}/\bar{\eta }_{eng}$ ， $\bar{\eta }_{mot}$ 为电机平均效率， $\bar{\eta }_{eng}$ 为发动机平均效率。目标函数由三部分构成，第一项为发动机燃油消耗量，与电池SOC无关，第二项为电机消耗的能量转化为等效的燃油消耗，第三项为维持电池SOC平衡的惩罚函数。

   式(13)两边分别对SOC进行求导，得到：

(14)

    结合式(14)和式(11)，可以推导出：

(15)

   由式(15)可以看出，等效因子调整规则包含两部分：一部分与发动机能量转化效率和电机能量转化效率有关，即![\bar{\eta}_{s(t)}=\bar{\eta }_{mot}/\bar{\eta }_{eng}](https://latex.codecogs.com/gif.latex?%5Cbar%7B%5Ceta%7D_%7Bs%28t%29%7D%3D%5Cbar%7B%5Ceta%20%7D_%7Bmot%7D/%5Cbar%7B%5Ceta%20%7D_%7Beng%7D)。而效率与发动机、电机的工作点有关，不同的工作点对应了不同的效率。因此，要实现对![\bar{\eta}_{s(t)}](https://latex.codecogs.com/gif.latex?%5Cbar%7B%5Ceta%7D_%7Bs%28t%29%7D)的精确估计是十分困难的，通常采用平均效率估计等效因子初始值。另一部分是与电池SOC有关，考虑维持电池SOC平衡。若实际SOC值低于参考SOC值，则相应增加等效因子，更多使用燃油，反之，亦然。显然，![\bar{\eta}_{s(t)}](https://latex.codecogs.com/gif.latex?%5Cbar%7B%5Ceta%7D_%7Bs%28t%29%7D)与工况有着密切的关系，随着工况的不同，发动机、电机工作点势必不同，导致![\bar{\eta}_{s(t)}](https://latex.codecogs.com/gif.latex?%5Cbar%7B%5Ceta%7D_%7Bs%28t%29%7D)发生变化。换言之，当针对某一个工况设计![\bar{\eta}_{s(t)}](https://latex.codecogs.com/gif.latex?%5Cbar%7B%5Ceta%7D_%7Bs%28t%29%7D)的能够取得优化结果时，对于另一个工况并非适用。因此，综合考虑工况对等效因子的影响是十分重要的。

   进一步地，对式(15)进行改写，可以得到：

(16)

其中， $s_{0}$ 为初始等效因子， $k_{p}$ ， $k_{i}$ 为常数因子， $SOC_{ref}$ 为参考SOC。对于本项目的混合动力汽车，参考SOC即初始SOC值。

    由上面的分析可知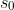，![s_{0}](https://latex.codecogs.com/gif.latex?s_%7B0%7D)的估计是关键，但是实际过程中难以精确估计出。因此，需对等效因子进行调整。对等效因子的调整既要考虑电池SOC平衡，又要兼顾工况对其的影响，以适应工况的变化。

2.2.2 等效因子构建——方法二

   为使 ECMS 控制策略得到较好的经济性能，等效因子的求解尤为关键。本项目中提出了另一种等效因子计算方法，先根据车辆的动力参数确定初值范围，然后再求其精确值。

等效因子下限
```
由能量守恒定律可知：
```

(17)

其中， $E_{fuel}$ 和 $E_{batt}$ 分别为整个行程过程中消耗的燃油能量和电池能量； $E_{dmd}$ 和 $E_{loss}$ 分别为完成行程需求的能量和损失的能量。在整个驾驶循环过程中，为减少能量消耗，使能量损失最小，即：

(18)

   由于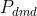![P_{dmd}](https://latex.codecogs.com/gif.latex?P_%7Bdmd%7D)是已知量，上式可简化为：

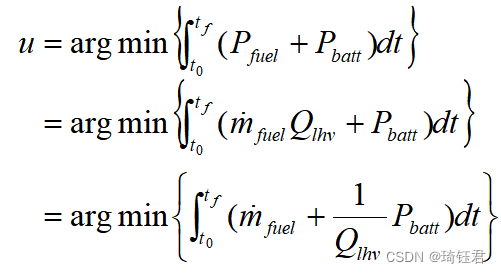
(19)

   与式(10)对比，可得到：

(20)

   从上面的推论可知，若SOC未超过其限值，则最优等效因子为 1。然而，在实际推导过程中未考虑SOC的限制，所以计算的值不一定适合。同时，仿真计算发现，当![s(t)=1](https://latex.codecogs.com/gif.latex?s%28t%29%3D1)时，电池SOC快速达到其最低限值，当![s(t)<1](https://latex.codecogs.com/gif.latex?s%28t%29%3C1)时，电池的放电率更大，几乎和纯电模式相当，其瞬时燃油经济性不再最优。因此，为获得最优的等效因子，其值应大于等于 1，即

(21)

等效因子上限

HEV有 5 种工作模式，可以用控制空间U来表示：

(21)

其中， $u_{fom}$ 代表发动机单独驱动模式； $u_{bom}$ 代表电机单独驱动模式； $u_{hm}$ 代表混合驱动模式； $u_{cm}$ 代表行车充电模式； $u_{bm}$ 代表制动能量回收模式。

    假设在某个时刻![P_{dmd}>0](https://latex.codecogs.com/gif.latex?P_%7Bdmd%7D%3E0)，且电池SOC达到最大限值![SOC_{max}](https://latex.codecogs.com/gif.latex?SOC_%7Bmax%7D)，即![SOC=SOC_{max}](https://latex.codecogs.com/gif.latex?SOC%3DSOC_%7Bmax%7D)，此时 ECMS 需要找到最优的控制模式![u^{*}](https://latex.codecogs.com/gif.latex?u%5E%7B*%7D)以减小成本函数。于是有:

(23)

   如果![s(t)](https://latex.codecogs.com/gif.latex?s%28t%29)的值太大，![u^{*}](https://latex.codecogs.com/gif.latex?u%5E%7B*%7D)更趋向于![\left \{ u_{fom} \right \}](https://latex.codecogs.com/gif.latex?%5Cleft%20%5C%7B%20u_%7Bfom%7D%20%5Cright%20%5C%7D)，当![s(t)](https://latex.codecogs.com/gif.latex?s%28t%29)的值无限大，车辆将一直工作在发动机单独工作模式。很显然，太大的 ![s(t)](https://latex.codecogs.com/gif.latex?s%28t%29)值，不会得到最优的解。因此，电机单独驱动模式或混合驱动模式都有可能使系统能量消耗最低，即:

(24)

     为计算最大值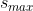![s_{max}](https://latex.codecogs.com/gif.latex?s_%7Bmax%7D)，式(24)将产生两个限值：![s_{max1}](https://latex.codecogs.com/gif.latex?s_%7Bmax1%7D)和![s_{_{max2}}](https://latex.codecogs.com/gif.latex?s_%7B_%7Bmax2%7D%7D)，则等效因子的上限为：

(25)

    求解式( 24)中第一个不等式：

(26)

其中， $\eta _{eng}$ 、 $\eta _{mot}$ 、 $\eta _{inv}$ 、 $\eta _{batt}$ 分别为发动机、电机、电机控制器和电池的效率。

   由于式(24)中的第2个不等式相关参数不能消去，故不能确定![s_{max2}^{*}](https://latex.codecogs.com/gif.latex?s_%7Bmax2%7D%5E%7B*%7D)具体的数值。好在最优的等效因子只须满足式( 24)中任一不等式即可。因此，本项目选择![s_{max1}^{*}](https://latex.codecogs.com/gif.latex?s_%7Bmax1%7D%5E%7B*%7D)的值作为最优协调变量的上限。对![s_{max1}^{*}](https://latex.codecogs.com/gif.latex?s_%7Bmax1%7D%5E%7B*%7D)的值进行简化，用平均效率来代替实际效率，于是得到最优协调变量的上限为：

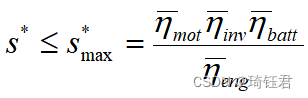
(27)

其中， $\bar{\eta }_{eng}$ 、 $\bar{\eta }_{mot}$ 、 $\bar{\eta }_{inv}$ 、 $\bar{\eta }_{batt}$ 分别为发动机、电机、电机控制器和电池的平均效率。

    结合式(21) 和式( 27) ，最优等效因子的界限为：

(28)

    故等效因子可以改为：

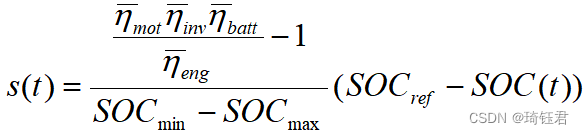
(29)

2.2.3 等效因子构建——方法三

   ECMS控制策略中的等效因子对于维持并联混合动力汽车的SOC平衡以及实现最佳燃油经济性起到了至关重要的作用。因此，根据汽车的行驶工况对等效因子进行动态管理，获得当前行驶工况下的最适合的时变等效因子![s(t)](https://latex.codecogs.com/gif.latex?s%28t%29)显得尤为重要。时变等效因子可以改为：

(30)

其中， $SOC_{min}$ 为 SOC 最小值， $SOC_{max}$ 为 SOC 最大值， $SOC_{ref}$ 为 SOC 参考值；n为指数系数。

2.3 控制策略具体应用

   本项目采用网格化扫描计算方法，即先确定系统约束条件和控制量的取值范围，并且离散化控制变量，求解网格点对应的目标函数可能取值，再求解使得目标函数最小时对应的控制量。具体流程如下：

 1. 已知发动机转矩外特性、燃油消耗率，电机转矩外特性、电机效率，可分别表示 ![T_{eng,max}=f_{T_{eng,max}}(\omega _{eng})](https://latex.codecogs.com/gif.latex?T_%7Beng%2Cmax%7D%3Df_%7BT_%7Beng%2Cmax%7D%7D%28%5Comega%20_%7Beng%7D%29),![BSFC=f_{BSFC}(T_{eng},\omega_{eng})](https://latex.codecogs.com/gif.latex?BSFC%3Df_%7BBSFC%7D%28T_%7Beng%7D%2C%5Comega_%7Beng%7D%29),![T_{mot,max}=f_{T_{mot,max}}(\omega _{mot})](https://latex.codecogs.com/gif.latex?T_%7Bmot%2Cmax%7D%3Df_%7BT_%7Bmot%2Cmax%7D%7D%28%5Comega%20_%7Bmot%7D%29),![T_{mot,min}=f_{T_{mot,min}}(\omega _{mot})](https://latex.codecogs.com/gif.latex?T_%7Bmot%2Cmin%7D%3Df_%7BT_%7Bmot%2Cmin%7D%7D%28%5Comega%20_%7Bmot%7D%29),![\eta_{mot}=f_{\eta_{mot}}(T_{mot},\omega _{mot})](https://latex.codecogs.com/gif.latex?%5Ceta_%7Bmot%7D%3Df_%7B%5Ceta_%7Bmot%7D%7D%28T_%7Bmot%7D%2C%5Comega%20_%7Bmot%7D%29)；

   2.  确定系统的约束条件，分别确定发动机、电机转速范围。相应地，由于发动机、电机特性数据通过试验获得，故通过插值方法求取当前转速点对应的发动机、电机特性数据；

3.确定电机转矩的可行域 $[T_{eng,min},T_{eng,max}]$ ，并且划分为N等份 $[T_{eng,min},\cdots,T_{eng,i},\cdots,T_{eng,max}]$ 。N的选择既要保证获得优化解，又减少计算量。若N选择太小，可能得不到优化解；若 N 选择太大，则计算量较大。本文根据电机的转矩范围，综合选取 N=200。然后，获得相应的电机转矩可能取值 $T_{mot,i}=T_{dmd}-T_{eng,i}$ ( $T_{dmd}$ 为驱动需求转矩)；

计算相应的发动机功率 $P_{eng,i}$ 、电机功率 $P_{mot,i}$ 及发动机燃油消耗 $\dot{m}_{fuel,i}=(BSFC\cdot P_{eng,i}\cdot 0.001)/3600$ ;
1. 计算相应的等效燃油消耗量 $\dot{m}_{_{equ,i}}=\dot{m}_{fuel,i}+s(t)\cdot P_{mot,i}/42500$ ；并求解最小等效燃油消耗量 $\dot{m}_{equ,min}=min\left \{ \dot{m}_{equ,1} ,\dot{m}_{equ,2},\cdots ,\dot{m}_{equ,i}\right \}$ ，获得对应的优化发动机机转矩 $T_{eng,opt}$ ，进而根据求出优化的电机转矩 $T_{mot,opt}=T_{dmd}-T_{eng,opt}$ 。ECMS求解流程如图4所示。

图4 ECMS实现流程图

3 仿真实验及结果分析

   为验证基于等效燃油消耗最小的能量控制策略的优化效果，以典型循环工况为例进行仿真实验。图5为车速跟随情况曲线。图6 为挡位工作情况。图7为电池SOC运动轨迹。图8为发动机转速工作情况。图9为发动机转矩工作情况。

图 5 车速跟随情况

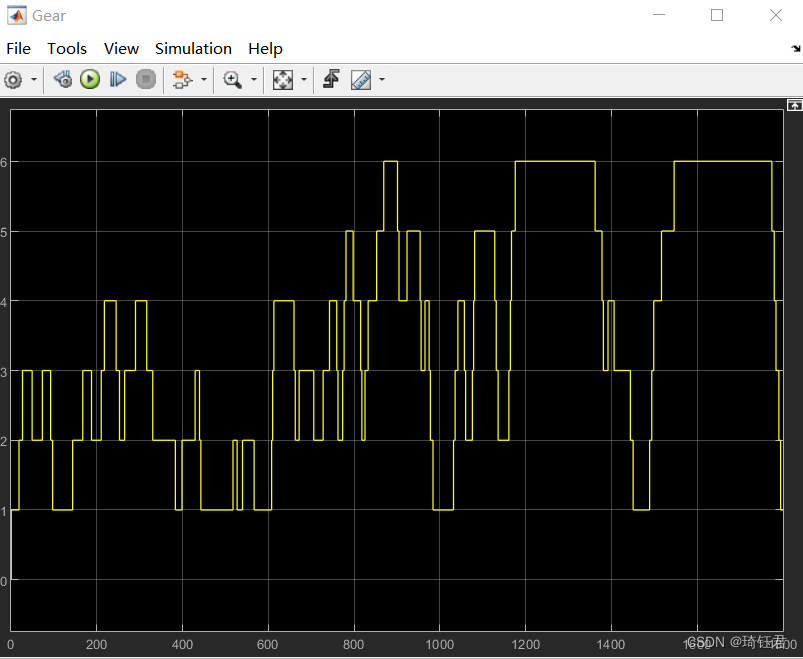
图 6 挡位变化情况

图 7 电池SOC运动轨迹

图 8 发动机转速工作曲线

图 9 发动机转矩工作曲线

由图5-9可见，发动机基本都工作在经济区域，电池SOC保持在一定的范围之内。

4 结论

   本项目以提高并联式混合动力汽车燃油经济性为目标，根据该系统结构特点和对控制策略的适应性要求，设计了以发动机转矩为控制变量，整车燃油消耗最小为目标的等效燃油消耗最小控制策略，并基于所建模型和策略进行了仿真。仿真结果表明：本项目所提出的控制策略的优化效果良好，发动机运行在高效区域内，电池能量也能保持平衡。

标签：汽车算法人工智能

本文转载自: https://blog.csdn.net/Jimmkudo/article/details/128102865
版权归原作者 琦钰君 所有，如有侵权，请联系我们删除。