1. 混合矩阵介绍
预测1
预测0
实际1
TP
FN
实际0
FP
TN
- TP (True Positive):实际为正,预测为正。
- FP(False Positive):实际为负,预测为正。
- TN (True Negative):实际为负,预测为负。
- FN (False Negative):实际为正,预测为负。
2. 模型评估方法
2.1 准确度
Accurray使用范围广,计算容易,但容易造假,即很容易训练一个准确较高的但用处不大的模型。如正样本90,负样本10个,直接把样本全部判正,则准确度90%,实际是没有意义的。
2.2. F1-score
- 精准率precision = TP / (TP + FP),即被分类器判正的数据中正样本占比,对象是模型判定结果。用于判断是否有误判。
- 召回率recall = TP / (TP + FN),即正样本数据中被模型判正的占比,对象是所有正样本数据。用于判断是否有漏判。
F1-score计算的是precision和recall的调和平均数,综合考量了模型查全率和查准率的计算结果,结果更偏向于较小的那个。
2.3 ROC & AUC
定义两个概念:伪阳率FPR和真阳率TPR
伪阳率FPR = FP / (FP + TN)
真阳率TPR = TP / (TP + FN)
ROC(Receiver Operating Characteristic)曲线,即在二维平面画的曲线-ROC curve,横坐标为FPR(false positive ratio),纵坐标为TPR。针对一个分类器,取不同的阈值,可以得到多组(FPR,TPR),即可绘制ROC曲线。由橙色曲线可知,曲线越靠近左上角,说明分类器效果越好;如果在对角线附近,则说明分类器接近随机猜测。

AUC(Area under ROC curve)是ROC曲线的数值化表示,即曲线下的面积大小,通常取值范围为[0.5, 1](如果在对角线下侧,则反向分析),值越大则表明分类器效果越好。
AUC = 1,是完美分类器,分类器不管选择哪个阈值均能完美分类。
0.5 < AUC < 1,优于随机猜测,分类器合理设置阈值,具有预测价值。
AUC = 0.5,随机猜测,分类没有预测价值。
AUC < 0.5,比随机猜测还差;但反预测而行,效果优于随机猜测。
建议值:AUC取值>0.7模型才有意义。
2.4 KS曲线
KS曲线即为KS值分布曲线,一般使用曲线最大值作为模型的评估结果,值越大,模型越具有区分能力。
- <= 20,模型无区分能力
20 & <= 40, 模型具有一定的预测能力。
40 & <= 60, 模型预测能力较为突出。
60 & <= 75,模型预测能力非常突出。
75 模型预测能力难以置信,需要评估验证。
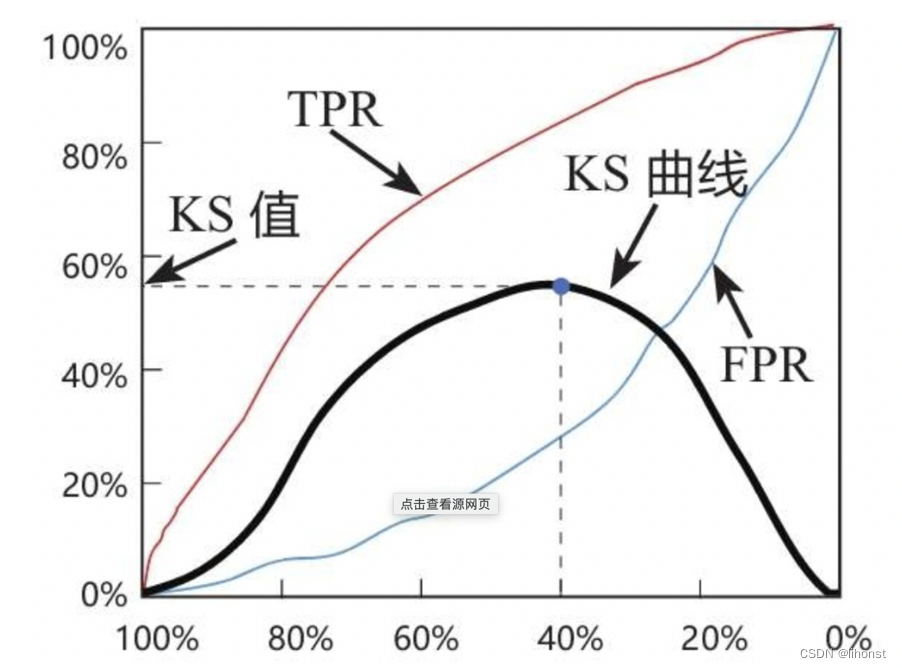
KS和AUC区别,两者都是通过TPR和FPR计算,KS取的是TPR与FPR差值的最大值,对于分类器能够找到一个合理的阈值;而AUC没有指定如何划分使模型效果最好,只是评估了模型的整体训练效果。
2.5 均方根误差(RMSE)/标准误差
在介绍RMSE前先介绍一下均方误差(MSE),它是通过模型预测值和实际值之间的距离的平方来衡量模型的效果,预测值和实际值越接近则模型效果越好。计算公式如下:
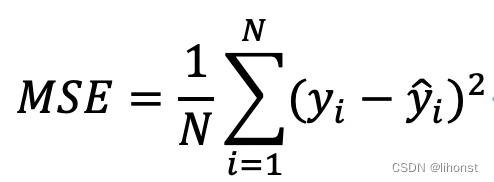
其中, N是训练集的个数,*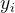*为每个训练集的真实输出,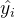为模型对每个训练数据的预测结果。
而均方根误差也即标准差,是均方误差的算术平方根。引入标准差的目的是解决均方误差的结果和实际数据的量纲不同问题,则RMSE的公式如下:
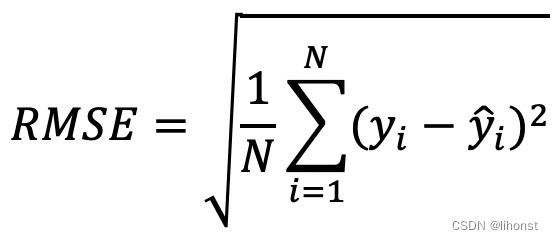
版权归原作者 lihonst 所有, 如有侵权,请联系我们删除。