神经网络和深度学习中的激活函数在激发隐藏节点以产生更理想的输出方面起着重要作用。激活函数的主要目的是将非线性特性引入模型。

在人工神经网络中，给定一个输入或一组输入，节点的激活函数定义该节点的输出。可以将标准集成电路视为激活功能的控制器，根据输入的不同，激活功能可以是“ ON”或“ OFF”。

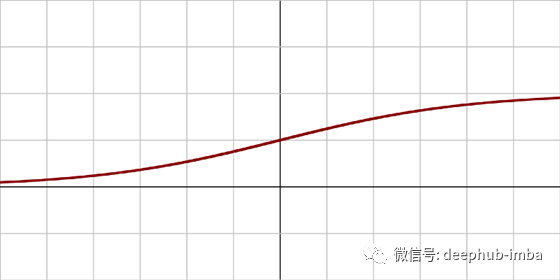
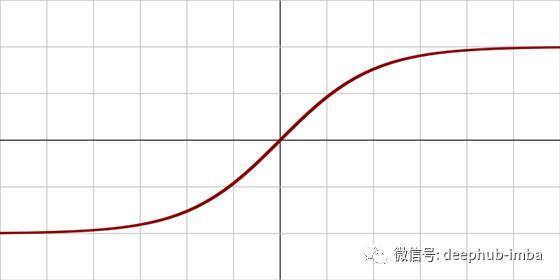
Sigmoid和tanh是单调、可微的激活函数，是在RELU出现以前比较流行的激活函数。然而，随着时间的推移，这些函数会遭受饱和，这导致出现梯度消失的问题。解决这一问题的另一种和最流行的激活函数是直线修正单元(ReLU)。

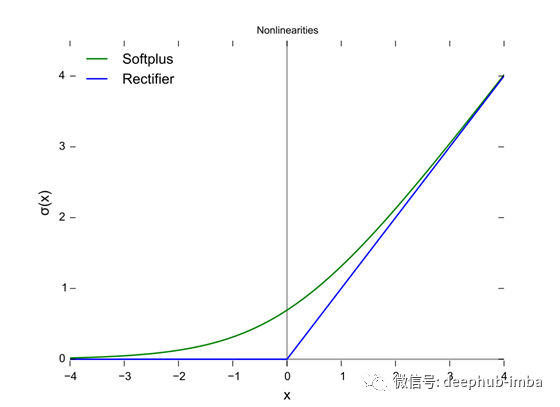
上面的图中用蓝线表示的是直线单元(ReLU)，而绿线是ReLU的变体，称为Softplus。ReLU的其他变体包括Leaky ReLU、ELU、SiLU等，用于提高某些任务的性能。

在本文中，我们只考虑直线单元(ReLU)，因为默认情况下，它仍然是执行大多数深度学习任务最常用的激活函数。它的变体通常用于特定的目的，在那里他们可能有轻微的优势在ReLU。

这个激活函数是Hahnloser等人在2000年首次引入到一个动态网络中，具有很强的生物学动机和数学证明。与2011年之前广泛使用的激活函数，如logistic sigmoid(灵感来自于概率理论和logistic回归)及其更实用的tanh（对应函数双曲正切）相比，2011年首次证明了该函数能够更好地训练更深层次的网络。

截止到2017年，整流器是深度神经网络中最受欢迎的激活函数。采用整流器的单元也称为整流线性单元(ReLU)。

RELU的最大问题是它在点0处是不可微的。而研究人员倾向于使用可微函数，例如S型和tanh。但是在0点可微这种情况毕竟还是特殊情况，所以到目前为止ReLU还是深度学习的最佳激活功能，毕竟他需要的计算量是非常小的，计算速度很快。

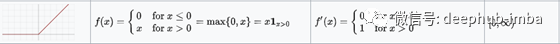
ReLU激活函数在除0点外的所有点都是可微的。对于大于0的值，我们只考虑函数的最大值。可以这样写:

f(x) = max{0, z}

简单地说，也可以这样写:

if input > 0:    
return input
else:    
return 0

所有负数默认为0，并考虑正数的最大值。

对于神经网络的反向传播计算，ReLU的判别相对容易。我们唯一要做的假设是在点0处的导数，也被认为是0。这通常不是一个大问题，而且在大多数情况下都能很好地工作。函数的导数就是斜率的值。负值的斜率是0.0，正值的斜率是1.0。

ReLU激活函数的主要优点是:

• 卷积层和深度学习:它们是卷积层和深度学习模型训练中最常用的激活函数。
• 计算简单:整流函数实现起来很简单，只需要一个max()函数。
• 代表性稀疏性:整流器函数的一个重要优点是它能够输出一个真正的零值。
• 线性行为:当神经网络的行为是线性或接近线性时，它更容易被优化。

然而，经过RELU单元的主要问题是所有的负值会立即变为零，这降低了模型对数据正确拟合或训练的能力。

这意味着任何给ReLU激活函数的负输入都会立即将图中的值变为零，这反过来会影响结果图，因为没有适当地映射负的值。不过，通过使用ReLU激活函数的不同变体(如Leaky ReLU和前面讨论的其他函数)，可以很容易地修复这个问题。

总结

这是一个简短的介绍，以了解整流线性单元及其重要性，在深度学习技术的今天。它比所有其他激活函数更流行，这是有原因的。

作者：Bharath K

deephub翻译组