当使用LSTM进行时间序列预测时,人们容易陷入一个常见的陷阱。为了解释这个问题,我们需要先回顾一下回归器和预测器是如何工作的。预测算法是这样处理时间序列的:

一个回归问题是这样的:
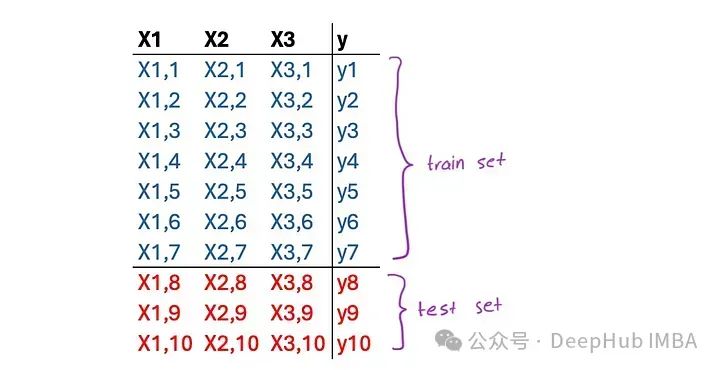
因为LSTM是一个回归量,我们需要把时间序列转换成一个回归问题。有许多方法可以做到这一点,一般使用窗口和多步的方法,但是在使用过程中会一个常见错误。
在窗口方法中,时间序列与每个时间步长的先前值相耦合,作为称为窗口的虚拟特征。这里我们有一个大小为3的窗口:
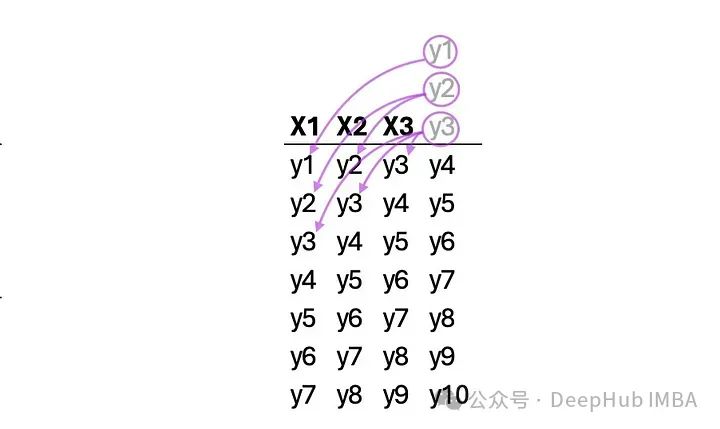
下面的函数从单个时间序列创建一个Window方法数据集。结果数据集将具有对角线重复,并且根据回看值,样本数量将发生变化:
def window(sequences, look_back):
X, y = [], []
for i in range(len(sequences)-look_back-1):
x = sequences[i:(i+look_back)]
X.append(x)
y.append(sequences[i + look_back])
return np.array(X), np.array(y)
让我们来检查一下结果。模型训练完成后,在测试集上进行测试。让我们看看代码和结果是什么样子的:
look_back = 3
X, y = window(ts_data, look_back)
# Train-test split
train_ratio = 0.8
train_size = int(train_ratio * len(ts_data))
X_train, X_test = X[:train_size-look_back], X[train_size-look_back:]
y_train, y_test = y[:train_size-look_back], y[train_size-look_back:]
# Create and train LSTM model
model = Sequential()
model.add(LSTM(units=72, activation='tanh', input_shape=(look_back, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='Adam', metrics=['mape'])
model.fit(x=X_train, y=y_train, epochs=500, batch_size=18, verbose=2)
# Make predictions
forecasts = model.predict(X_test)
lstm_fits = model.predict(X_train)
# Calculate metrics
mape = mean_absolute_percentage_error(y_test, forecasts)
r2 = r2_score(y_train, lstm_fits)
# Initialize dates
date_range = pd.date_range(start='1990-01-01', end='2023-09-30', freq='M')
# Add empty values in fits to match the original time series
fits = np.full(train_size, np.nan)
for i in range(train_size-look_back):
fits[i+look_back] = lstm_fits[i]
# Plot actual, fits, and forecasts
plt.figure(figsize=(10, 6))
plt.plot(date_range, ts_data, label='Actual', color='blue')
plt.plot(date_range[:train_size], fits, label='Fitted', color='green')
plt.plot(date_range[train_size:], forecasts, label='Forecast', color='red')
plt.title('FSC - Short - Passengers\nOne Step Forward Forecast')
plt.xlabel('Date')
plt.ylabel('Passengers')
plt.legend()
plt.text(0.05, 0.05, f'R2 = {r2*100:.2f}%\nMAPE = {mape*100:.2f}%', transform=plt.gca().transAxes, fontsize=12)
plt.grid(True)
plt.show()

结果看起来很棒。但是看一下样本测试集,我们发现了一个奇怪的问题:

在生成y9时,y8在模型中被用作输入。但是实际上我们是不知道y8的值的,我们正在预测未来的时间步骤,将未来的值也纳入其中了。
所以用前一个实例的预测值替换输入值的迭代测试集将解决问题。但是在这种情况下,模型建立在自己的预测之上,就像传统的预测算法一样:

# Iterative prediction and substitution
for i in range(len(X_test)):
forecasts[i] = model.predict(X_test[i].reshape(1, look_back, 1))
if i != len(X_test)-1:
X_test[i+1,look_back-1] = forecasts[i]
for j in range(look_back-1):
X_test[i+1,j] = X_test[i,j+1]
结果就变成了这样:
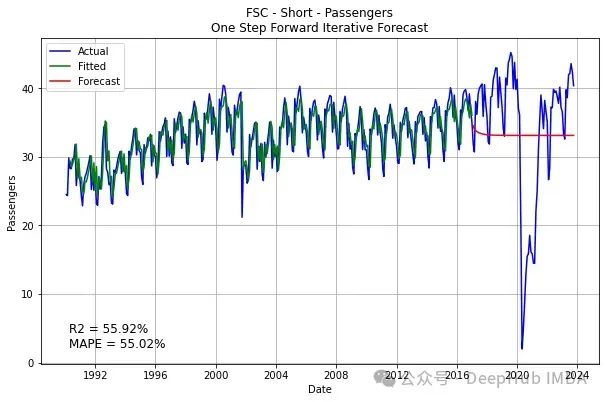
出现这种结果的一个主要原因是误差的放大,y8是预测的结果,本身就会产生误差,在误差的基础上预测y9就又会产生更大的误差,这样所得到的误差就会被一步一步的放大。
多步骤方法类似于窗口方法,但有更多的目标步骤。以下是两个步骤的示例:

对于这个方法,必须选择n_steps_in和n_steps_out。下面的代码将一个简单的时间序列转换成一个准备进行多步LSTM训练的数据集:
# split a univariate sequence into samples with multi-steps
def split_sequences(sequences, n_steps_in, n_steps_out):
X, y = list(), list()
for i in range(len(sequences)):
# find the end of this pattern
end_ix = i + n_steps_in
out_end_ix = end_ix + n_steps_out
# check if we are beyond the sequence
if out_end_ix > len(sequences):
break
# gather input and output parts of the pattern
seq_x, seq_y = sequences[i:end_ix], sequences[end_ix:out_end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
不仅特征和目标都有对角线重复,这意味着要与时间序列进行比较,我们要么取平均值,要么选择一个预测。在下面的代码中,生成了第一、最后和平均预测的结果,需要注意的是,这里的第一次预测是提前一个月预测,最后一次预测是提前12个月预测。
n_steps_in = 12
n_steps_out = 12
X, y = split_sequences(ts_data, n_steps_in, n_steps_out)
X = X.reshape(X.shape[0], X.shape[1], 1)
y = y.reshape(y.shape[0], y.shape[1], 1)
# Train-test split
train_ratio = 0.8
train_size = int(train_ratio * len(ts_data))
X_train, X_test = X[:train_size-n_steps_in-n_steps_out+1], X[train_size-n_steps_in-n_steps_out+1:]
y_train = y[:train_size-n_steps_in-n_steps_out+1]
y_test = ts_data[train_size:]
# Create and train LSTM model
model = Sequential()
model.add(LSTM(units=72, activation='tanh', input_shape=(n_steps_in, 1)))
model.add(Dense(units=n_steps_out))
model.compile(loss='mean_squared_error', optimizer='Adam', metrics=['mape'])
model.fit(x=X_train, y=y_train, epochs=500, batch_size=18, verbose=2)
# Make predictions
lstm_predictions = model.predict(X_test)
lstm_fitted = model.predict(X_train)
forecasts = [np.diag(np.fliplr(lstm_predictions), i).mean() for i in range(0, -lstm_predictions.shape[0], -1)]
fits = [np.diag(np.fliplr(lstm_fitted), i).mean() for i in range(lstm_fitted.shape[1]+n_steps_in - 1, -lstm_fitted.shape[0], -1)]
forecasts1 = lstm_predictions[n_steps_out-1:,0]
fits1 = model.predict(X)[:train_size-n_steps_in,0]
forecasts12 = lstm_predictions[:,n_steps_out-1]
fits12 = lstm_fitted[:,n_steps_out-1]
# Metrics
av_mape = mean_absolute_percentage_error(y_test, forecasts)
av_r2 = r2_score(ts_data[n_steps_in:train_size], fits[n_steps_in:])
one_mape = mean_absolute_percentage_error(y_test[:-n_steps_out+1], forecasts1)
one_r2 = r2_score(ts_data[n_steps_in:train_size], fits1)
twelve_mape = mean_absolute_percentage_error(y_test, forecasts12)
twelve_r2 = r2_score(ts_data[n_steps_in+n_steps_out-1:train_size], fits12)
date_range = pd.date_range(start='1990-01-01', end='2023-09-30', freq='M')
# Plot actual, fits, and forecasts
plt.figure(figsize=(10, 6))
plt.plot(date_range, ts_data, label='Actual', color='blue')
plt.plot(date_range[:train_size], fits, label='Fitted', color='green')
plt.plot(date_range[train_size:], forecasts, label='Forecast', color='red')
plt.title('FSC - Short - Passengers\n. LSTM 12 Month Average Forecast')
plt.xlabel('Date')
plt.ylabel('Passengers')
plt.legend()
plt.text(0.05, 0.05, f'R2 = {av_r2*100:.2f}%\nMAPE = {av_mape*100:.2f}%', transform=plt.gca().transAxes, fontsize=12)
plt.grid(True)
plt.show()
plt.figure(figsize=(10, 6))
plt.plot(date_range, ts_data, label='Actual', color='blue')
plt.plot(date_range[n_steps_in:train_size], fits1, label='Fitted', color='green')
plt.plot(date_range[train_size:-n_steps_out+1], forecasts1, label='Forecast', color='red')
plt.title('FSC - Short - Passengers\n LSTM 1 Month in advance Forecast')
plt.xlabel('Date')
plt.ylabel('Passengers')
plt.legend()
plt.text(0.05, 0.05, f'R2 = {one_r2*100:.2f}%\nMAPE = {one_mape*100:.2f}%', transform=plt.gca().transAxes, fontsize=12)
plt.grid(True)
plt.show()
plt.figure(figsize=(10, 6))
plt.plot(date_range, ts_data, label='Actual', color='blue')
plt.plot(date_range[n_steps_in+n_steps_out-1:train_size], fits12, label='Fitted', color='green')
plt.plot(date_range[train_size:], forecasts12, label='Forecast', color='red')
plt.title('FSC - Short - Passengers\n LSTM 12 Months in advance Forecast')
plt.xlabel('Date')
plt.ylabel('Passengers')
plt.legend()
plt.text(0.05, 0.05, f'R2 = {twelve_r2*100:.2f}%\nMAPE = {twelve_mape*100:.2f}%', transform=plt.gca().transAxes, fontsize=12)
plt.grid(True)
plt.show()

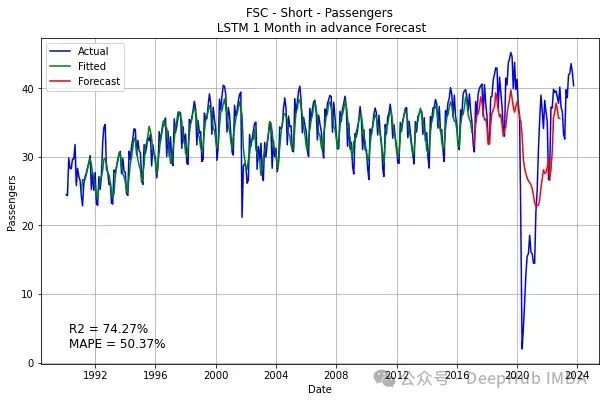
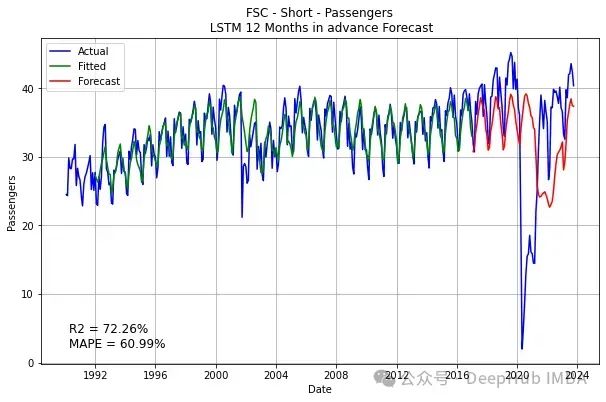
同样的问题仍然存在这里:

那么上面的问题如何解决呢?
我们可以采用与在Window Method中所做的类似的方法。但是选择另一个方向,选择n_step_out与test_size相同。通过这种方式,测试集缩小到只有一个:
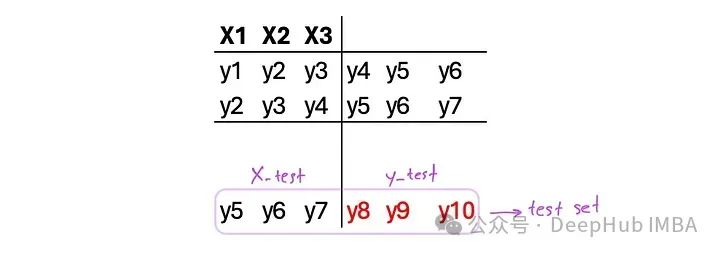
下面的函数就是这样做的。它需要时间序列、训练大小和样本数量。我把它称作可比性,因为这个版本实际上可以与其他预测算法进行比较:
def split_sequences_comparable(sequences, n_samples, train_size):
# Steps
n_steps_out = len(sequences) - train_size
n_steps_in = train_size - n_steps_out - n_samples + 1
# End sets
X_test = sequences[n_samples + n_steps_out - 1:train_size]
X_forecast = sequences[-n_steps_in:]
X, y = list(), list()
for i in range(n_samples):
# find the end of this pattern
end_ix = i + n_steps_in
out_end_ix = end_ix + n_steps_out
# gather input and output parts of the pattern
seq_x, seq_y = sequences[i:end_ix], sequences[end_ix:out_end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y), np.array(X_test), np.array(X_forecast), n_steps_in, n_steps_out
上面的这个函数,n_steps_out是固定的,所以可以由参数来选择样本的数量和训练的大小,它会计算最大可能的n_steps_in。下面是执行的代码和结果:
n_samples = 12
train_size = 321
X, y, X_test, X_forecast, n_steps_in, n_steps_out = split_sequences_comparable(ts_data, n_samples, train_size)
y_test = ts_data[train_size:]
# Reshaping
X = X.reshape(X.shape[0], X.shape[1], 1)
X_test = X_test.reshape(X_test.shape[1], X_test.shape[0], 1)
y = y.reshape(y.shape[0], y.shape[1])
y_test = y_test.reshape(y_test.shape[1], y_test.shape[0], 1)
# Create and train LSTM model
model = Sequential()
model.add(LSTM(units=154, activation='tanh', input_shape=(n_steps_in, 1)))
model.add(Dense(units=n_steps_out))
model.compile(loss='mean_squared_error', optimizer='Adam', metrics=['mape'])
model.fit(x=X, y=y, epochs=500, batch_size=18, verbose=2)
# Make predictions
lstm_predictions = model.predict(X_test)
predictions = lstm_predictions.reshape(lstm_predictions.shape[1])
lstm_fitted = model.predict(X)
fits = [np.diag(np.fliplr(lstm_fitted), i).mean() for i in range(lstm_fitted.shape[1]+n_steps_in - 1, -lstm_fitted.shape[0], -1)]
# Metrics
mape = mean_absolute_percentage_error(y_test, predictions)
r2 = r2_score(ts_data[n_steps_in:train_size], fits[n_steps_in:])
# Plot actual, fits, and forecasts
plt.figure(figsize=(10, 6))
plt.plot(date_range, ts_data, label='Actual', color='blue')
plt.plot(date_range[:train_size], fits, label='Fitted', color='green')
plt.plot(date_range[train_size:], predictions, label='Forecast', color='red')
plt.title('FSC - Short - Passengers\n12 Sample Comparable LSTM Forecast')
plt.xlabel('Date')
plt.ylabel('Passengers')
plt.legend()
plt.text(0.05, 0.05, f'R2 = {r2*100:.2f}%\nMAPE = {mape*100:.2f}%\', transform=plt.gca().transAxes, fontsize=12)
plt.grid(True)
plt.show()
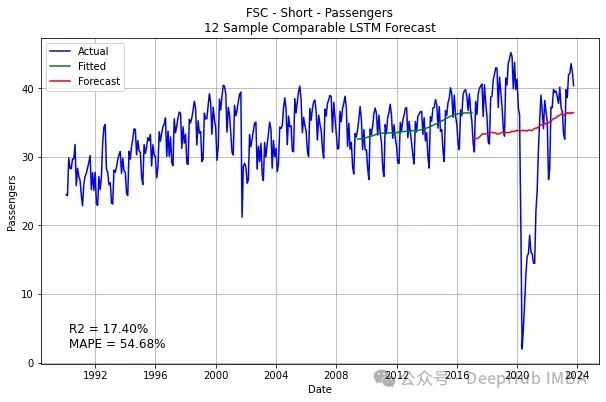
结果虽然不是很满意,但是我们看到了代码已经预测了一些上升的趋势,要比前面的一条直线好一些,但是这里LSTM将所有时间步长聚合到特征中,所有这些方法都会丢失时间数据,所以在后面将介绍(编码器/解码器方法)来维护输入的时间结构,解决这一问题。
作者:Seyed Mousavi