一、算法简介
粒子群算法(Particle swarm optimization, PSO)是一种仿生算法,它是一种 在求解空间中寻找最优解 的简单算法。它与其他优化算法的不同之处在于,它只需要 目标函数,不依赖于目标的梯度或任何微分形式。它也有很少的超参数。
由Kennedy和Eberhart于1995年提出;
群体迭代,粒子(partical)在解空间追随最优的粒子进行搜索;
PSO和差分演化算法已成为现代优化方法领域研究的热点
粒子群算法是一门新兴算法,此算法与遗传算法有很多相似之处,其收敛于全局最优解的概率很大。
①相较于传统算法计算速度非常快,全局搜索能力也很强;
②PSO对于种群大小不十分敏感,所以初始种群设为500-1000,速度影响也不大;
③粒子群算法适用于连续函数极值问题,对于非线性、多峰问题均有较强的全局搜索能力。
算法优点:
①简单易行;②收敛速度快;③设置参数少
算法基本思想:
PSO思想源于对鸟类捕食行为的研究;
模拟鸟集群飞行觅食的行为,鸟之间通过集体的协作使种群达到最优目的是一种基于Swarm Intelligence的优化方法;
PSO结合了社会行为(Social-only model)和个体认知(Cognition-only model)
算法介绍:
①每个寻优的问题都被想象成一只鸟,称为粒子。所有粒子都在一个n维空间进行搜索。
②所有粒子都由一个fitness function确定适应值以判断目前位置的好坏
③每一个粒子必须赋予记忆功能,以记住所搜寻到的最佳位置。
④每一个粒子还有一个速度(velocity)以决定飞行的距离和方向。这个速度根据它本身飞行经验以及同伴的飞行经验进行动态调整。
相关概念:
群体(Swarm):粒子的集合,相当于遗传算法的种群
粒子(Partical):群体中的搜索个体
位置(Position);速度(Velocity);当前粒子自身最优位置(Individual best position):Pbest
群体全局最优位置(Global best position):Gbest
二、算法流程
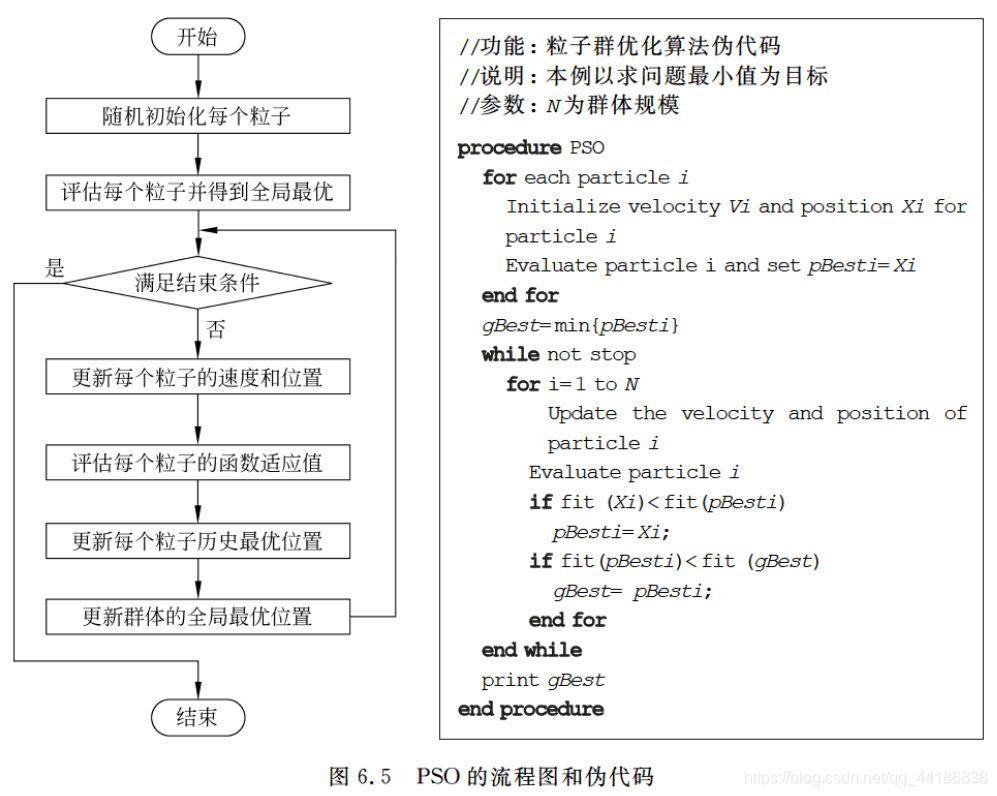
三、PSO构成要素
群体大小(NP)
NP是一个整数;
NP很小时,陷入局部最优的可能性很大;
NP很大时,PSO的优化能力很好,但算法收敛慢;
当群体数目增长至一定水平时,再增长将不再有显著作用;
惯性权重因子(w)
w是一个非负数;
w=1基本PSO算法
w=0失去粒子本身的速度记忆
个体认知常数(c1)
c1=0无私型PSO,“只有社会,没有自我”;
迅速失去群体多样性,易陷入局部最优而无法跳出;
社会经验常数(c2)
c2=0自私性PSO,“只有自我,没有社会”;
完全没有信息的社会共享,导致算法收敛速度缓慢
最大速度(Vmax)
用于维护算法的勘探能力和开采能力的平衡
Vmax较大时,勘探能力强,但粒子容易飞过最优解;
Vmax较小时,开采能力强,但容易陷入局部最优解;
Vmax一般设为每维变量变化范围的10%-20%
邻域(Neighborhood)拓扑结构
在PSO算法中,一个粒子的邻域表示群体中与该粒子相邻的粒子的集合,粒子可以与其邻域中的粒子交换信息,邻域的规模决定了信息交换的范围。一个粒子的邻域可以是整个群体,也可以由其周围的少数几个粒子构成,邻域拓扑决定了群体中粒子的相邻关系。三种主要的邻域拓扑:星状拓扑(也称全局邻域拓扑)、坏状拓扑和轮状拓扑。
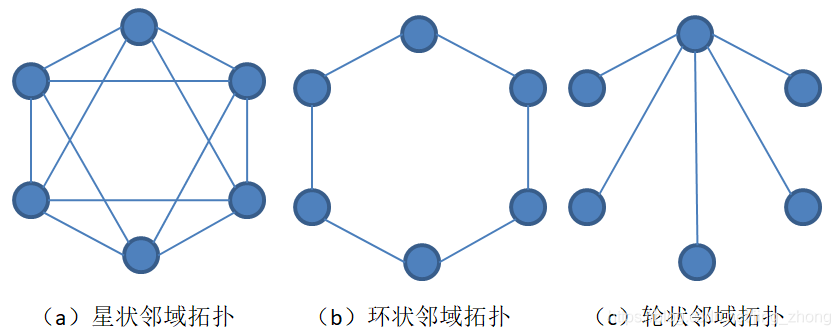
当邻域结构取为全局邻域结构时,粒子pi的局部极值gi成为全局极值,通常记为gbest。
通过对以上三种邻域结构进行实验研究,Kennedy得出的结论是:
使用全局邻域结构的PSO算法收敛速度较快,但容易陷入局部最优;
使用环状邻域结构的PSO算法的收敛速度较慢,但能以较大的概率发现最优解;
而使用轮状邻域结构的PSO算法效果较差。
全局历史最优解:Gbest;
局部历史最优解:Lbest;
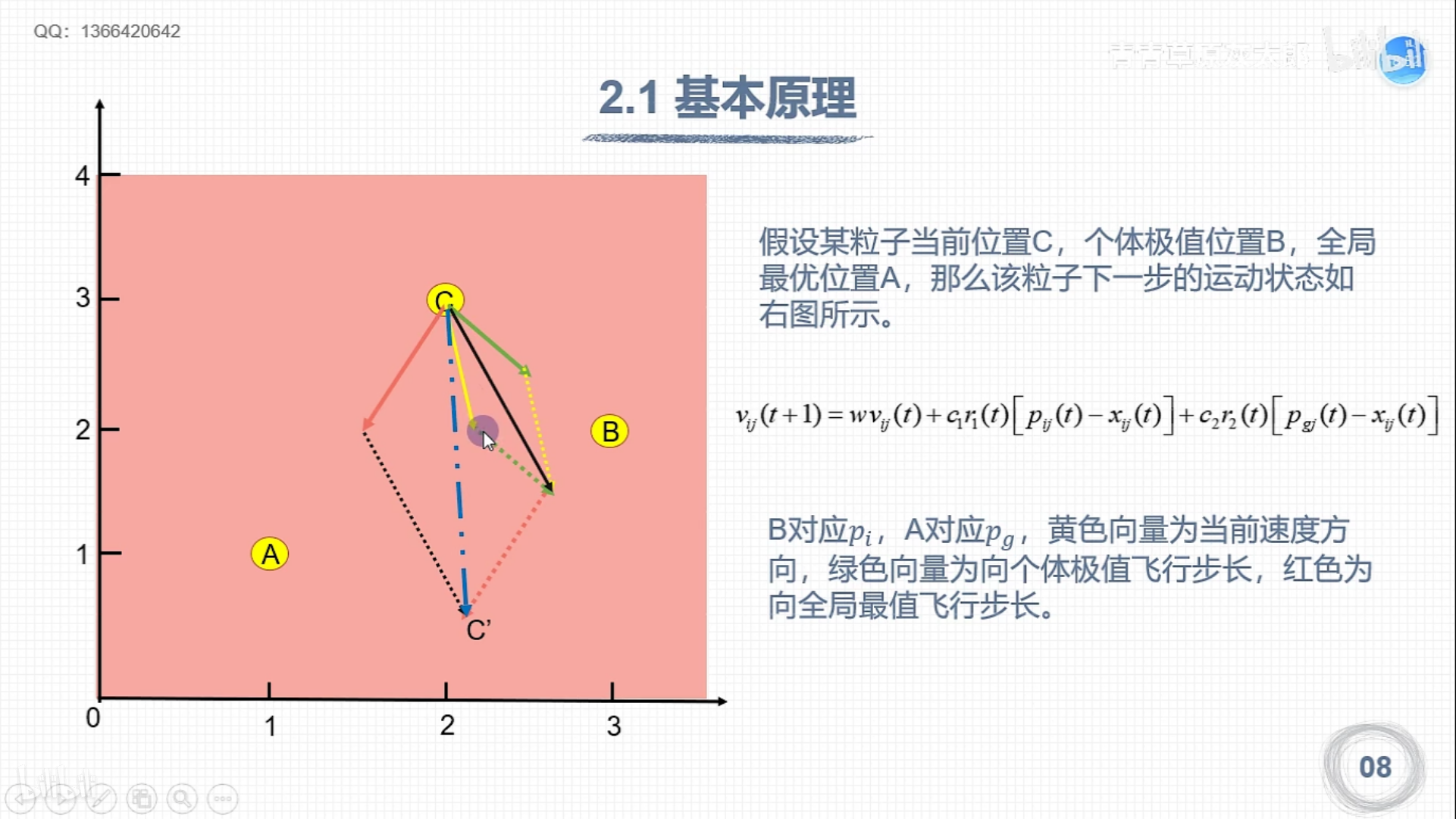
不同于遗传算法,粒子群算法不需要编码,直接利用粒子的位置来表示自变量,每个粒子的位置都由自变量的个数和取值范围决定,而速度由自变量的个数和速度限制决定,形式如下,其中d代表空间维数(自变量数):


step4处错误,应改为根据粒子的适应值来更新个体的历史极值并计算全局极值。


应用举例:

粒子群优化算法改进研究

以函数xsin(x)cos(2x)-2xcos(3x)+3xsin(4x)为例
位置和速度的初始化即在位置和速度限制内随机生成一个N x d 的矩阵,对于此题,位置初始化也就是在050内随机生成一个20x1的数据矩阵,而对于速度则不用考虑约束,一般直接在01内随机生成一个20x1的数据矩阵
粒子群的另一个特点就是记录每个个体的历史最优和种群的历史最优,因此而二者对应的最优位置和最优值也需要初始化。其中每个个体的历史最优位置可以先初始化为当前位置,而种群的历史最优位置则可初始化为原点。对于最优值,如果求最大值则初始化为负无穷,相反地初始化为正无穷。
每次搜寻都需要将当前的适应度和最优解同历史的记录值进行对比,如果超过历史最优值,则更新个体和种群的历史最优位置和最优解。
每次更新完速度和位置都需要考虑速度和位置的限制,需要将其限制在规定范围内,此处仅举出一个常规方法,即将超约束的数据约束到边界(当位置或者速度超出初始化限制时,将其拉回靠近的边界处)。当然,你不用担心他会停住不动,因为每个粒子还有惯性和其他两个参数的影响。
clear
%函数表达式,求解这个函数的最大值
f=@(x)x.*sin(x).*cos(2*x)-2*x.*sin(3*x)+3*x.*sin(4*x);
N=20;%初始种群个数
d=1;%可行解维数
ger=200;%最大迭代次数
limit=[0,50];%设置位置参数限制 即x范围
vlimit=[-10,10];%设置速度限制
w=0.8;%惯性权重
c1=0.5;%自我学习因子
c2=0.5;%群体学习因子
figure(1);ezplot(f,[0,0.01,limit(2)]);
x=limit(1)+(limit(2)-limit(1)).*rand(N,d);%初始化种群位置
% rand() 函数用于生成一个或多个 0 到 1 之间的随机数。
% 调用 rand() 函数时,如果不带参数,则返回一个 0 到 1 之间的随机数;
% 如果带一个参数,则返回一个该参数指定大小的矩阵,其中包含 0 到 1 之间的随机数。
% 如果带两个参数,则返回一个该参数指定大小的矩阵,其中包含 0 到 1 之间的随机数。
v=rand(N,d);%初始化种群速度
xm=x;%每个个体的历史最佳位置
ym=zeros(1,d);%种群的历史最佳位置
fxm=ones(N,1)*inf;%每个个体的历史最佳适应度 inf是表示无穷大
fym=inf;%种群历史最佳适应度
%hold on是当前轴及图像保持而不被刷新,准备接受此后将绘制的图形,多图共存,
%即启动图形保持功能,当前坐标轴和图形都将保持,
%从此绘制的图形都将添加在这个图形的基础上,并自动调整坐标轴的范围
%hold off使当前轴及图像不再具备被刷新的性质,新图出现时,取消原图。即关闭图形保持功能。
hold on
plot(xm,f(xm),'ro');
title('初始状态图');
figure(2)
%群体更新
iter=1;
%record=zeros(ger,1);%记录器
while iter<=ger
fx=f(x);%个体当前适应度
for i=1:N
if fx(i)<fxm(i)
fxm(i)=fx(i);%更新个体历史最佳适应度
xm(i,:)=x(i,:);%更新个体历史最佳位置
end
end
if min(fxm)<fym
[fym,nmin]=min(fxm);%更新群体历史最佳适应度
ym=xm(nmin,:);
end
%先更新速度,再更新位置
v=v*w+c1*rand*(xm-x)+c2*rand*(repmat(ym,N,1)-x);%速度更新,rempat函数是矩阵的复制函数
%xm是行向量,ym是一个数
%边界速度处理
v(v>limit(2))=vlimit(2);
v(v<limit(1))=vlimit(1);
x=x+v;%位置更新
%边界位置处理
x(x>limit(2))=limit(2);
x(x<limit(1))=limit(1);
record(iter)=fym;%最大值记录
x0=0:0.01:limit(2);
subplot(1,2,1);%一行两列的第一个图
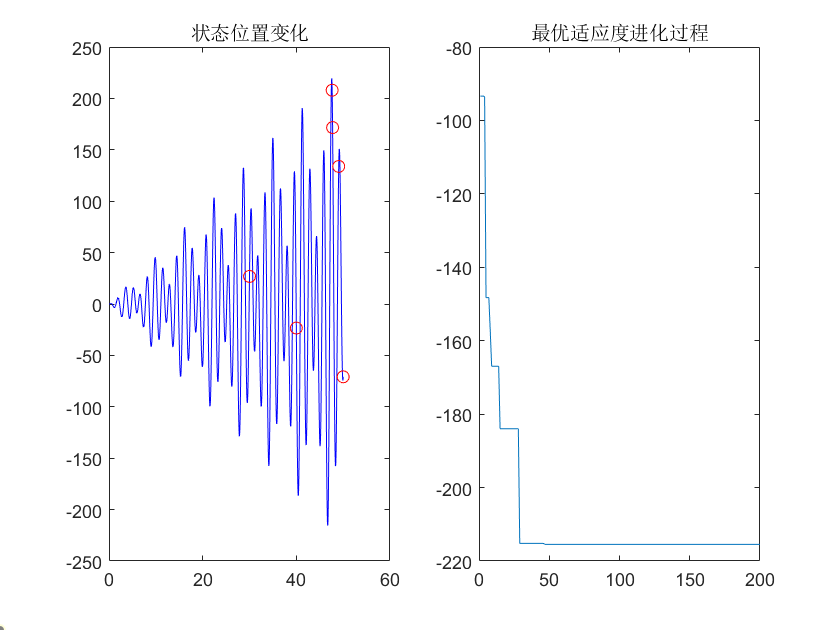
plot(x0,f(x0),'b-',x,f(x),'ro');title('状态位置变化')
subplot(1,2,2);%一行两列的第二个图
plot(record);title('最优适应度进化过程')
pause(0.05);%pause(n)暂停执行n秒,然后继续执行。必须启用暂停,此调用才能生效。
iter=iter+1;
end
x0=0:0.01:limit(2);
figure(3);
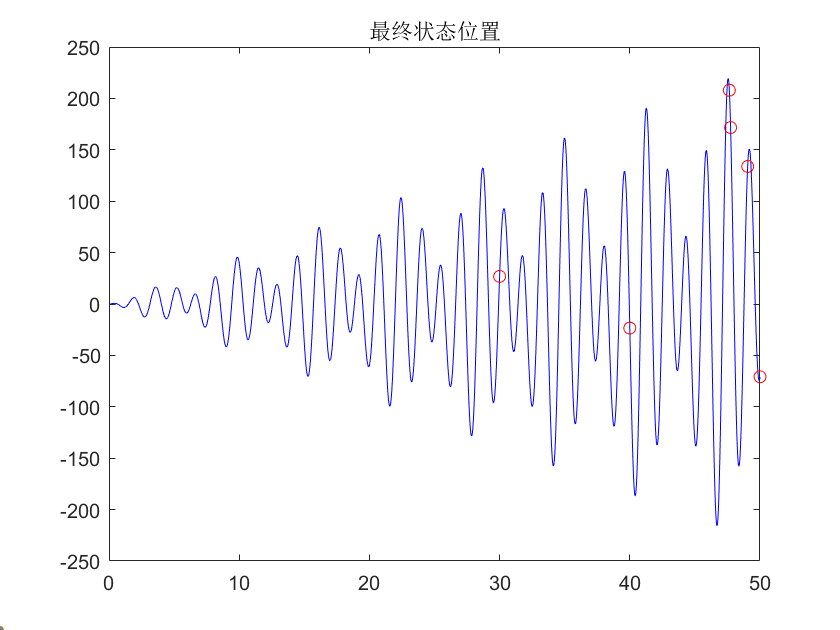
plot(x0,f(x0),'b-',x,f(x),'ro');title('最终状态位置')
%disp函数会直接将内容输出在Matlab命令窗口中
% 同时输出字符串和数字:
disp(['最小值:',num2str(fym)]);
disp(['变量取值:',num2str(ym)]);
最终结果:
最小值:-215.4596
变量取值:46.7056
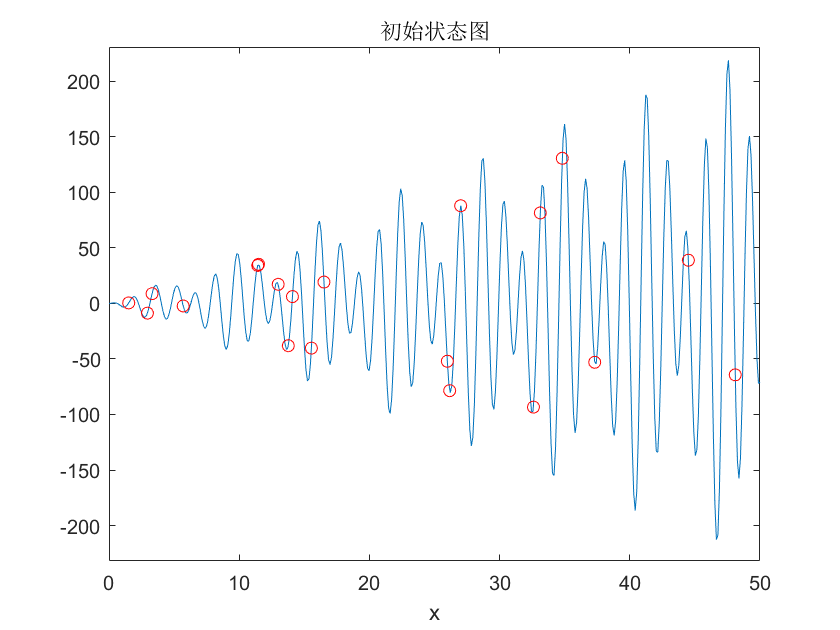
待求解问题:
Rosenbrock’s,取值范围为[-10,10],取值范围内的理想最优解为0,将其搜索的空间维度设为20。
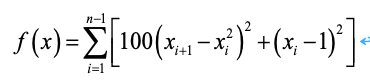
#库的导入
import numpy as np
import random
import matplotlib.pyplot as plt
#待求解问题
def function(x):
y1 = 0
for i in range(len(x) - 1):
y2 = 100 * ((x[i + 1] - x[i] ** 2) ** 2) + (x[i] - 1) ** 2
y1 = y1 + y2
y = abs(0 - y1)
return y
rangepop=[-10,10] #取值范围
pn=30 #种群数量
iterators = 1000 #迭代次数
w=0.9 #惯性因子
#两个加速系数
c1=2
c2=2
#a1用于存储种群个体位置信息,v用于存储种群个体移动速度,fitness用于存储个体适应度值
a1=np.zeros((pn,20))
v = np.zeros((pn, 20))
fitness=np.zeros(pn)
#对种群个体、移动速度进行初始化,计算初始适应度值
for j in range(pn):
a1[j] = np.random.uniform(low=-10, high=10,size=(1, 20))
v[j] = np.zeros((1,20))
fitness[j] = function(a1[j])
#allpg,bestpg分别表示种群历史最优个体和适应度值
allpg,bestpg=a1[fitness.argmin()].copy(),fitness.min()
#poppn,bestpn分别存储个体历史最优位置和适应度值
poppn,bestpn=a1.copy(),fitness.copy()
#bestfitness用于存储每次迭代时的种群历史最优适应度值
bestfitness=np.zeros(iterators)
#开始迭代
for i in range(iterators):
print("generation:",i)
for m in range(pn):
r1 = np.random.rand()
r2 = np.random.rand()
#计算移动速度
v[m]=w*v[m]+c1*r1*(poppn[m]-a1[m])+c2*r2*(allpg-a1[m])
#计算新的位置
a1[m]=a1[m]+v[m]
#确保更新后的位置在取值范围内
a1[a1<rangepop[0]]=rangepop[0]
a1[a1>rangepop[1]]=rangepop[1]
#计算适应度值
fitness[m] = function(a1[m])
#更新个体历史最优适应度值
if fitness[m]<bestpn[m]:
bestpn[m]=fitness[m]
poppn[m]=a1[m].copy()
#更新种群历史最优适应度值
if bestpn.min()<bestpg:
bestpg=bestpn.min()
allpg=poppn[bestpn.argmin()].copy()
bestfitness[i]=bestpg
print("the best fitness is:",bestfitness[i])
#将结果进行绘图
fig=plt.figure(figsize=(12, 10), dpi=300)
plt.title('The change of best fitness',fontdict={'weight':'normal','size': 30})
x=range(1,1001,1)
plt.plot(x,bestfitness,color="red",label="PSO",linewidth=3.0, linestyle="-")
plt.tick_params(labelsize=25)
plt.xlabel("Epoch",fontdict={'weight':'normal','size': 30})
plt.ylabel("Fitness value",fontdict={'weight':'normal','size': 30})
plt.xticks(range(0,1001,100))
plt.legend(loc="upper right",prop={'size':20})
plt.savefig("PSO.png")
plt.show()

#include <iostream>
#include<time.h>
#include <random>
using namespace std;
//使用c++实现粒子群算法
//需要寻优的非线性函数为:
//f(x,y) = sin(sqrt(x^2+y^2))/(sqrt(x^2+y^2)) + exp((cos(2*PI*x)+cos(2*PI*y))/2) - 2.71289
//该函数有很多局部极大值点,而极限位置为(0,0),在(0,0)附近取得极大值
// Author: yuzewei
const int N = 20; //粒子群数量
const int dim = 2; //粒子群维度
const int gen = 300;//100; //迭代次数
const double PI = 3.1415926;
const double w = 0.9;//0.6; //惯性权重
const double c1 = 2;// 1.49445; //自学习,学习因子
const double c2 = 2; // 1.49445; //群体最优学习,学习因子
const double pmin = -2.0; //粒子的移动区间范围
const double pmax = 2.0;
const double vmin = -0.8;// -0.5; //粒子的移动速度范围
const double vmax = 0.8;// 0.5;
double P[N][dim]; //粒子位置
double V[N][dim]; //粒子速度
double fitness[N]; //粒子适应度
double pbest[N][dim]; //粒子最优位置
double gbest[dim]; //粒子群最优位置
int gbestGen = -1; //记录达到最优位置时的迭代次数
double func(double *p)
{
double x = *p;
double y = *(p + 1);
double result = sin(sqrt(x * x + y * y)) / (sqrt(x * x + y * y))
+ exp((cos(2 * PI * x) + cos(2 * PI * y)) / 2) - 2.71289;
return result;
}
int getGbestIndex(double *fit)
{
int index = -1;
double max = *fit;
for (int i = 0; i < N; i++)
{
if (*(fit + i) > max)
{
max = *(fit + i);
index = i;
}
}
return index;
}
void init()
{
int index = -1; //记录位置最佳的粒子编号
default_random_engine e;
uniform_real_distribution<double> rand1(pmin, pmax);
uniform_real_distribution<double> rand2(vmin, vmax);
e.seed(time(0));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < dim; j++)
{
P[i][j] = rand1(e);
V[i][j] = rand2(e);
pbest[i][j] = P[i][j];
}
fitness[i] = func(P[i]);
}
index = getGbestIndex(fitness);
gbest[0] = pbest[index][0];
gbest[1] = pbest[index][1];
gbestGen = 0;
}
void printParticles()
{
/*for (int i = 0; i < N; i++)
{
cout << "第" << i << "个粒子" << endl;
cout << " 位置:(" << P[i][0] << "," << P[i][1] << ")" << endl;
cout << " 速度:(" << V[i][0] << "," << V[i][1] << ")" << endl;
cout << " 适应度:" << fitness[i] << endl;
cout << " 个体最优:(" << pbest[i][0] << "," << pbest[i][1] << ")" << endl;
}*/
//cout << endl;
cout<<"群体最优:(" << gbest[0] << "," << gbest[1] << ")" << endl;
cout << "适应度为:" << func(gbest) << endl;
}
void PSOiterator()
{
cout << "开始迭代!" << endl;
cout << "第1代粒子群:" << endl;
printParticles();
for (int g = 0; g < gen - 1; g++)
{
cout << "第" << g + 2 << "代粒子群:" << endl;
int index = -1; //记录最优粒子个体编号
default_random_engine e;
uniform_real_distribution<double> rand(0, 1.0);
e.seed(time(0));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < dim; j++)
{
//更新速度
V[i][j] = w * V[i][j] + rand(e) * (pbest[i][j] - P[i][j])
+ rand(e) * (gbest[j] - P[i][j]);
if (V[i][j] < vmin)
V[i][j] = vmin;
if (V[i][j] > vmax)
V[i][j] = vmax;
//更新位置
P[i][j] = P[i][j] + V[i][j];
if (P[i][j] < pmin)
P[i][j] = pmin;
if (P[i][j] > pmax)
P[i][j] = pmax;
}
fitness[i] = func(P[i]); //更新适应度
//更新个体最优
if (fitness[i] > func(pbest[i]))
{
pbest[i][0] = P[i][0];
pbest[i][1] = P[i][1];
}
}
//更新整体最优
index = getGbestIndex(fitness);
if (func(P[index]) > func(gbest))
{
gbest[0] = P[index][0];
gbest[1] = P[index][1];
gbestGen = g + 1;
}
printParticles();
}
}
void printResult()
{
cout << "迭代结束!" << endl;
cout << "总共进行了" << gen << "次迭代,";
cout<<"第"<<gbestGen<<"代得到最优位置:(" << gbest[0] << "," << gbest[1] << ")" << endl;
cout << "此位置对应的函数值为:" << func(gbest) << endl;
}
int main()
{
init();
PSOiterator();
printResult();
return 0;
}
版权归原作者 想不到名字222 所有, 如有侵权,请联系我们删除。