多智能体强化学习—QMIX

多智能体强化学习—QMIX

论文地址：https://arxiv.org/pdf/1803.11485.pdf

1 介绍

  首先介绍一下VDN（value decomposition networks）顾名思义，VDN是一种价值分解的网络，采用对每个智能体的值函数进行整合，得到一个联合动作值函数。
为了简单阐述考虑两个智能体：（o-observations，a-actions，Q-action-value function）

  当智能体观察他自己的目标时，但不一定是队友的目标，那么有：

  当(

     o
    
    
     i
    
   
   
    ,
   
   
    
     a
    
    
     i
    
   
  
  
   o^i,a^i
  
 
oi,ai)不足以完全建模

 
  
   
    
     
      Q
     
     
      ˉ
     
    
    
     i
    
    
     π
    
   
   
    (
   
   
    s
   
   
    ,
   
   
    a
   
   
    )
   
  
  
   \bar{Q}_{i}^{\pi}(\mathbf{s}, \mathbf{a})
  
 
Qˉ​iπ​(s,a),利用LSTM网络的历史观测获取额外信息（t时刻看到目标A，t+5时刻目标A被挡住了，利用t+5时刻的观测数据无法获得目标A的有效信息，只有利用历史观测数据从新定位目标A）

 
  
   
    
     
      Q
     
     
      π
     
    
    
     (
    
    
     s
    
    
     ,
    
    
     a
    
    
     )
    
    
     =
    
    
     :
    
    
     
      
       Q
      
      
       ˉ
      
     
     
      1
     
     
      π
     
    
    
     (
    
    
     s
    
    
     ,
    
    
     a
    
    
     )
    
    
     +
    
    
     
      
       Q
      
      
       ˉ
      
     
     
      2
     
     
      π
     
    
    
     (
    
    
     s
    
    
     ,
    
    
     a
    
    
     )
    
    
     ≈
    
    
     
      
       Q
      
      
       ~
      
     
     
      1
     
     
      π
     
    
    
     
      (
     
     
      
       h
      
      
       1
      
     
     
      ,
     
     
      
       a
      
      
       1
      
     
     
      )
     
    
    
     +
    
    
     
      
       Q
      
      
       ~
      
     
     
      2
     
     
      π
     
    
    
     
      (
     
     
      
       h
      
      
       2
      
     
     
      ,
     
     
      
       a
      
      
       2
      
     
     
      )
     
    
   
   
    Q^{\pi}(\mathbf{s}, \mathbf{a})=: \bar{Q}_{1}^{\pi}(\mathbf{s}, \mathbf{a})+\bar{Q}_{2}^{\pi}(\mathbf{s}, \mathbf{a}) \approx \tilde{Q}_{1}^{\pi}\left(h^{1}, a^{1}\right)+\tilde{Q}_{2}^{\pi}\left(h^{2}, a^{2}\right)
   
  
 Qπ(s,a)=:Qˉ​1π​(s,a)+Qˉ​2π​(s,a)≈Q~​1π​(h1,a1)+Q~​2π​(h2,a2)

  值分解网络旨在学习一个联合动作值函数

     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    (
   
   
    τ
   
   
    ,
   
   
    u
   
   
    )
   
  
  
   Q_{t o t}(\tau,u)
  
 
Qtot​(τ,u) ，其中 

 
  
   
    τ
   
   
    ∈
   
   
    T
   
   
    ≡
   
   
    
     τ
    
    
     n
    
   
  
  
   \tau \in T \equiv \tau^{n}
  
 
τ∈T≡τn 是一个联合动作-观测的历史轨迹，

 
  
   
    u
   
  
  
   u
  
 
u是一个联合动作。它是由每个智能体 

 
  
   
    i
   
  
  
   i
  
 
i独立计算其值函数 

 
  
   
    
     Q
    
    
     i
    
   
   
    
     (
    
    
     
      τ
     
     
      i
     
    
    
     ,
    
    
     
      u
     
     
      i
     
    
    
     ;
    
    
     
      θ
     
     
      i
     
    
    
     )
    
   
  
  
   Q_{i}\left(\tau^{i}, u^{i} ; \theta^{i}\right)
  
 
Qi​(τi,ui;θi)，之后累加求和得到的。其关系如下所示：

 
  
   
    
     
      Q
     
     
      
       t
      
      
       o
      
      
       t
      
     
    
    
     =
    
    
     
      ∑
     
     
      
       i
      
      
       =
      
      
       1
      
     
     
      n
     
    
    
     
      Q
     
     
      i
     
    
    
     
      (
     
     
      
       τ
      
      
       i
      
     
     
      ,
     
     
      
       a
      
      
       i
      
     
     
      ;
     
     
      
       θ
      
      
       i
      
     
     
      )
     
    
   
   
    Q_{t o t}=\sum_{i=1}^{n} Q_{i}\left(\tau_{i}, a_{i} ; \theta_{i}\right)
   
  
 Qtot​=i=1∑n​Qi​(τi​,ai​;θi​)

具体请看原论文：https://arxiv.org/pdf/1706.05296.pdf

QMIX，和VDN类似，也是一种基于价值的方法，可以以集中的端到端方式训练分散策略。QMIX采用了一个网络，将联合动作值估计为每个智能体值的复杂非线性组合（VDN是线性加和），且仅基于局部观测。并且在结构上施加约束，使联合动作值函数与每个智能体动作值函数之间是单调的，保证集中策略和分散策略之间的一致性。
IGM（Individual-Global-Max）：

       argmax
      
      
       ⁡
      
     
     
      u
     
    
    
     
      Q
     
     
      
       t
      
      
       o
      
      
       t
      
     
    
    
     (
    
    
     τ
    
    
     ,
    
    
     u
    
    
     )
    
    
     =
    
    
     
      (
     
     
      
       
        
         
          
           argmax
          
          
           ⁡
          
          
           
            u
           
           
            1
           
          
         
        
       
       
        
         
          
           
            Q
           
           
            1
           
          
          
           
            (
           
           
            
             τ
            
            
             1
            
           
           
            ,
           
           
            
             u
            
            
             1
            
           
           
            )
           
          
         
        
       
      
      
       
        
         
          ⋮
         
         
          
         
        
       
      
      
       
        
         
          
           argmax
          
          
           ⁡
          
          
           
            u
           
           
            n
           
          
         
        
       
       
        
         
          
           
            Q
           
           
            n
           
          
          
           
            (
           
           
            
             τ
            
            
             n
            
           
           
            ,
           
           
            
             u
            
            
             n
            
           
           
            )
           
          
         
        
       
      
     
     
      )
     
    
   
   
     \underset{\mathbf{u}}{\operatorname{argmax}} Q_{t o t}(\tau, \mathbf{u})=\left(\begin{array}{cc} \operatorname{argmax}_{u^{1}} & Q_{1}\left(\tau^{1}, u^{1}\right) \\ \vdots \\ {\operatorname{argmax}}_{u^{n}} & Q_{n}\left(\tau^{n}, u^{n}\right) \end{array}\right) 
   
  
 uargmax​Qtot​(τ,u)=⎝⎜⎛​argmaxu1​⋮argmaxun​​Q1​(τ1,u1)Qn​(τn,un)​⎠⎟⎞​

  其中，

     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
  
  
   Q_{tot}
  
 
Qtot​表示联合Q函数；

 
  
   
    
     Q
    
    
     i
    
   
  
  
   Q_i
  
 
Qi​表示智能体 i的动作值函数。

IGM表示

    a
   
   
    r
   
   
    g
   
   
    m
   
   
    a
   
   
    x
   
   
    (
   
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    )
   
  
  
   argmax (Q_{tot})
  
 
argmax(Qtot​) 与

 
  
   
    a
   
   
    r
   
   
    g
   
   
    m
   
   
    a
   
   
    x
   
   
    (
   
   
    
     Q
    
    
     i
    
   
   
    )
   
  
  
   argmax (Q_i)
  
 
argmax(Qi​)得到相同结果，这表示在无约束条件的情况下，个体最优就代表整体最优。为了保证这一条件，QMIX以单调条件进行限制:

2 QMIX 算法框架

框架主要分三两部分：

• （a）混合网络结构（红色是超网络，为蓝色的混合网络层产生权重和偏差）
• （b）整体的QMIX架构
• （c）智能体网络结构

下面进行具体分析：

2.1 Agent network

输入：

    t
   
  
  
   t
  
 
t时刻智能体

 
  
   
    a
   
  
  
   a
  
 
a的观测值

 
  
   
    
     o
    
    
     t
    
    
     a
    
   
  
  
   o_t^a
  
 
ota​、

 
  
   
    t
   
   
    −
   
   
    1
   
  
  
   t-1
  
 
t−1时刻智能体

 
  
   
    a
   
  
  
   a
  
 
a的动作

 
  
   
    
     u
    
    
     
      t
     
     
      −
     
     
      1
     
    
    
     a
    
   
  
  
   u_{t-1}^a
  
 
ut−1a​

输出：

    t
   
  
  
   t
  
 
t时刻智能体

 
  
   
    a
   
  
  
   a
  
 
a的值函数

 
  
   
    
     Q
    
    
     a
    
   
   
    
     (
    
    
     
      τ
     
     
      a
     
    
    
     ,
    
    
     
      u
     
     
      t
     
     
      a
     
    
    
     )
    
   
  
  
   Q_{a}\left(\tau^{a}, u_t^{a}\right)
  
 
Qa​(τa,uta​)

  Agent network由DRQN网络实现，根据不同的任务需求，不同智能体的网络可以进行单独训练，也可进行参数共享，DRQN是将DQN中的全连接层替换为GRU网络，其循环层由一个具有64维隐藏状态的GRU组成，循环网络在观测质量变化的情况下，具有更强的适应性。如图所示，其网络一共包含 3 层，输入层（MLP多层神经网络)→ 中间层（GRU门控循环神经网络）→ 输出层（MLP多层神经网络）
实现代码如下：
智能体网络参数配置：

# --- Agent parameters ---
agent:"rnn"# Default rnn agent
rnn_hidden_dim:64# Size of hidden state for default rnn agent
obs_agent_id:True# Include the agent's one_hot id in the observation
obs_last_action:True# Include the agent's last action (one_hot) in the observation

RNN网络：

classRNNAgent(nn.Module):def__init__(self, input_shape, args):super(RNNAgent, self).__init__()
        self.args = args
        #根据参数配置，智能体网络的输入#input_shape = obs_shape + n_actions + one_hot_code（one_hot_code_o+one_hot_code_u）
        self.fc1 = nn.Linear(input_shape, args.rnn_hidden_dim)# 线性层
        self.rnn = nn.GRUCell(args.rnn_hidden_dim, args.rnn_hidden_dim)# GRU层，需要输入隐藏状态
        self.fc2 = nn.Linear(args.rnn_hidden_dim, args.n_actions)# 线性层definit_hidden(self):# make hidden states on same device as modelreturn self.fc1.weight.new(1, self.args.rnn_hidden_dim).zero_()defforward(self, inputs, hidden_state):
        x = F.relu(self.fc1(inputs))# 输入经过线性层后relu激活，输出x
        h_in = hidden_state.reshape(-1, self.args.rnn_hidden_dim)# 对隐藏状态进行变形，列数为隐藏层维度大小
        h = self.rnn(x, h_in)# 循环神经网络，输入x，与隐藏状态(上一时刻信息)
        q = self.fc2(h)# 输出Q值return q, h

2.2 Mixing network

输入：

    t
   
  
  
   t
  
 
t时刻智能体

 
  
   
    a
   
  
  
   a
  
 
a的值函数

 
  
   
    
     Q
    
    
     a
    
   
   
    
     (
    
    
     
      τ
     
     
      a
     
    
    
     ,
    
    
     
      u
     
     
      t
     
     
      a
     
    
    
     )
    
   
  
  
   Q_{a}\left(\tau^{a}, u_t^{a}\right)
  
 
Qa​(τa,uta​)、

 
  
   
    t
   
  
  
   t
  
 
t时刻全局状态

 
  
   
    s
   
  
  
   s
  
 
s

输出：

    t
   
  
  
   t
  
 
t时刻联合动作价值函数

 
  
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    
     (
    
    
     τ
    
    
     ,
    
    
     u
    
    
     )
    
   
  
  
   Q_{tot}\left(\tau, u\right)
  
 
Qtot​(τ,u)

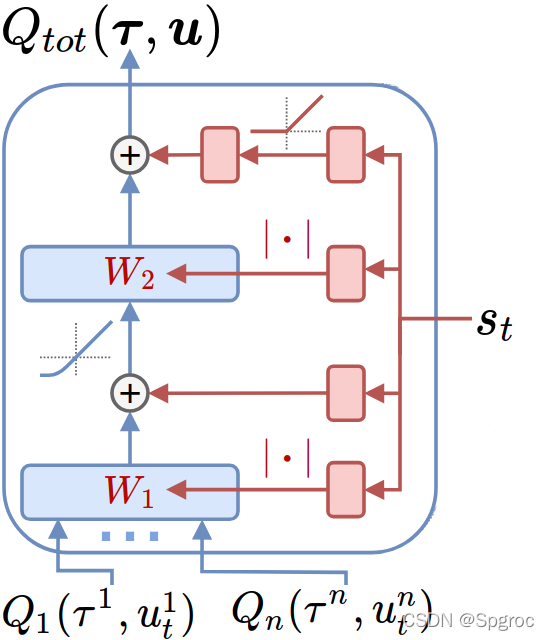
Mixing network是一个前馈神经网络，它以智能体网络的输出作为输入，单调地混合，产生

     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
  
  
   Q_{tot}
  
 
Qtot​的值，如图所示。为了保证的单调性约束，混合网络的权值

 
  
   
    w
   
   
    e
   
   
    i
   
   
    g
   
   
    h
   
   
    t
   
   
    s
   
  
  
   weights
  
 
weights被限制为非负值（偏差bias可以为负数）。这使得混合网络可以逼近任何单调函数。

混合网络的权值是由单独的超网络产生的。每个超网络以全局状态

    s
   
  
  
   s
  
 
s作为输入，生成一层混合网络的权值。每个超网络由一个单一的线性层组成，然后是一个绝对值激活函数，确保混合网络的权值是非负的。偏差也以同样的方式产生，但偏差的生成网络没有绝对值激活函数。最终的偏差是由一个具有ReLU非线性的2层超网络产生。

实现代码如下：

mixer:"qmix"
mixing_embed_dim:32
hypernet_layers:2
hypernet_embed:64

classQMixer(nn.Module):def__init__(self, args):super(QMixer, self).__init__()

        self.args = args
        self.n_agents = args.n_agents  # 智能体个数
        self.state_dim =int(np.prod(args.state_shape))# 状态维度

        self.embed_dim = args.mixing_embed_dim  # 网络内部嵌入维度ifgetattr(args,"hypernet_layers",1)==1:# 超网络的层数是否为1# 不包含隐层，只有一个线性层
            self.hyper_w_1 = nn.Linear(self.state_dim, self.embed_dim * self.n_agents)
            self.hyper_w_final = nn.Linear(self.state_dim, self.embed_dim)elifgetattr(args,"hypernet_layers",1)==2:# 超网络的层数是否为2
            hypernet_embed = self.args.hypernet_embed  # 超网络的嵌入层数# 因为生成的hyper_w1需要是一个矩阵，而pytorch神经网络只能输出一个向量，# 所以就先输出长度为需要的 矩阵行*矩阵列 的向量，然后再转化成矩阵# hyper_w1 网络用于输出推理网络中的第一层神经元所需的 weights
            self.hyper_w_1 = nn.Sequential(nn.Linear(self.state_dim, hypernet_embed),
                                           nn.ReLU(),
                                           nn.Linear(hypernet_embed, self.embed_dim * self.n_agents))# hyper_w_final 生成推理网络需要的从隐层到输出 Q 值的所有 weights，共 embed_dim 个
            self.hyper_w_final = nn.Sequential(nn.Linear(self.state_dim, hypernet_embed),
                                               nn.ReLU(),
                                               nn.Linear(hypernet_embed, self.embed_dim))elifgetattr(args,"hypernet_layers",1)>2:# 超网络层数进行判断raise Exception("Sorry >2 hypernet layers is not implemented!")else:raise Exception("Error setting number of hypernet layers.")#  hyper_b1 生成第一层网络对应维度的偏差 bias
        self.hyper_b_1 = nn.Linear(self.state_dim, self.embed_dim)#  V 生成对应从隐层到输出 Q 值层的 bias
        self.V = nn.Sequential(nn.Linear(self.state_dim, self.embed_dim),
                               nn.ReLU(),
                               nn.Linear(self.embed_dim,1))defforward(self, agent_qs, states):# 输入状态单个智能体的q值，全局状态s# states的shape为(episode_num, max_episode_len， state_shape)
        bs = agent_qs.size(0)# 传入的agent_qs是三维的，shape为(episode_num, max_episode_len， n_agents)
        states = states.reshape(-1, self.state_dim)# (episode_num * max_episode_len, state_shape)
        agent_qs = agent_qs.view(-1,1, self.n_agents)# (episode_num * max_episode_len, 1, n_agents)# First layer
        w1 = th.abs(self.hyper_w_1(states))# 获得参数w1，加绝对值，保证单调
        b1 = self.hyper_b_1(states)# 获得偏差b1
        w1 = w1.view(-1, self.n_agents, self.embed_dim)# 变换(episode_num, n_agents, embed_dim)
        b1 = b1.view(-1,1, self.embed_dim)# 变换(episode_num, 1, embed_dim)
        hidden = F.elu(th.bmm(agent_qs, w1)+ b1)# th.bmm矩阵乘法,输出到隐藏# Second layer
        w_final = th.abs(self.hyper_w_final(states))# 获得参数w2，加绝对值，保证单调
        w_final = w_final.view(-1, self.embed_dim,1)# 变换(episode_num, embed_dim, 1)# State-dependent bias
        v = self.V(states).view(-1,1,1)# 获得偏差b2(episode_num, 1, 1)# Compute final output
        y = th.bmm(hidden, w_final)+ v  # th.bmm矩阵乘法,得到最终数值# Reshape and return
        q_tot = y.view(bs,-1,1)# 变换(episode_num,1,1)return q_tot  # 得到Q_tot

2.3 算法更新流程

损失函数：

    L
   
   
    (
   
   
    θ
   
   
    )
   
   
    =
   
   
    
     ∑
    
    
     
      i
     
     
      =
     
     
      1
     
    
    
     b
    
   
   
    
     [
    
    
     
      
       (
      
      
       
        y
       
       
        i
       
       
        
         t
        
        
         o
        
        
         t
        
       
      
      
       −
      
      
       
        Q
       
       
        
         t
        
        
         o
        
        
         t
        
       
      
      
       (
      
      
       τ
      
      
       ,
      
      
       u
      
      
       ,
      
      
       s
      
      
       ;
      
      
       θ
      
      
       )
      
      
       )
      
     
     
      2
     
    
    
     ]
    
   
  
  
   \mathcal{L}(\theta)=\sum_{i=1}^{b}\left[\left(y_{i}^{t o t}-Q_{t o t}(\tau, \mathbf{u}, s ; \theta)\right)^{2}\right]
  
 
L(θ)=∑i=1b​[(yitot​−Qtot​(τ,u,s;θ))2]

其中

    b
   
  
  
   b
  
 
b表示从经验池中采样的样本数量，

 
  
   
    
     y
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    =
   
   
    r
   
   
    +
   
   
    γ
   
   
    
     
      max
     
     
      ⁡
     
    
    
     
      u
     
     
      ′
     
    
   
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    
     (
    
    
     
      τ
     
     
      ′
     
    
    
     ,
    
    
     
      u
     
     
      ′
     
    
    
     ,
    
    
     
      s
     
     
      ′
     
    
    
     ;
    
    
     
      θ
     
     
      −
     
    
    
     )
    
   
  
  
   y^{t o t}=r+\gamma \max _{\mathbf{u}^{\prime}} Q_{t o t}\left(\tau^{\prime}, \mathbf{u}^{\prime}, s^{\prime} ; \theta^{-}\right)
  
 
ytot=r+γmaxu′​Qtot​(τ′,u′,s′;θ−)，

 
  
   
    
     θ
    
    
     −
    
   
  
  
   \theta^{-}
  
 
θ−是目标网络的参数，

所以时序差分的误差可表示为：

          T
         
         
          D
         
         
          e
         
         
          r
         
         
          r
         
         
          o
         
         
          r
         
        
        
         =
        
        
         (
        
        
         r
        
        
         +
        
        
         γ
        
        
         
          Q
         
         
          
           t
          
          
           o
          
          
           t
          
         
        
        
         (
        
        
          target 
        
        
         )
        
        
         )
        
        
         −
        
        
         
          Q
         
         
          
           t
          
          
           o
          
          
           t
          
         
        
        
         (
        
        
          evalutate 
        
        
         )
        
       
      
     
    
   
   
    \begin{aligned} {TDerror}=(r+\gamma Q _{ tot }(\text { target })) -Q _{ tot }(\text { evalutate }) \end{aligned}
   
  
 TDerror=(r+γQtot​( target ))−Qtot​( evalutate )​


 
  
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    (
   
   
     target 
   
   
    )
   
  
  
   Q _{ tot }(\text { target })
  
 
Qtot​( target )：状态

 
  
   
    
     s
    
    
     
     
      ′
     
    
   
  
  
   s^{'}
  
 
s′的情况下，所有行为中，获取的最大价值

 
  
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
  
  
   Q_{tot}
  
 
Qtot​。根据IGM条件，输入为此状态下每个智能体的最大动作价值。


 
  
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
   
    (
   
   
     evalutate 
   
   
    )
   
  
  
   Q _{ tot }(\text { evalutate })
  
 
Qtot​( evalutate )： 状态

 
  
   
    s
   
  
  
   s
  
 
s的情况下，根据当前网络策略所能获得

 
  
   
    
     Q
    
    
     
      t
     
     
      o
     
     
      t
     
    
   
  
  
   Q_{tot}
  
 
Qtot​。

实现代码如下：
参数配置：

# use epsilon greedy action selector
action_selector:"epsilon_greedy"
epsilon_start:1.0
epsilon_finish:0.05
epsilon_anneal_time:50000

runner:"episode"

buffer_size:5000# update the target network every {} episodes
target_update_interval:200

动作选择：（ε-greedy）

classEpsilonGreedyActionSelector():def__init__(self, args):
        self.args = args

        self.schedule = DecayThenFlatSchedule(args.epsilon_start, args.epsilon_finish, args.epsilon_anneal_time,
                                              decay="linear")
        self.epsilon = self.schedule.eval(0)defselect_action(self, agent_inputs, avail_actions, t_env, test_mode=False):# Assuming agent_inputs is a batch of Q-Values for each agent bav
        self.epsilon = self.schedule.eval(t_env)# 获取epsilonif test_mode:# Greedy action selection only
            self.epsilon =0.0# mask actions that are excluded from selection
        masked_q_values = agent_inputs.clone()# q值 q_value
        masked_q_values[avail_actions ==0.0]=-float("inf")# should never be selected! 不能选择的动作赋值为 负无穷

        random_numbers = th.rand_like(agent_inputs[:,:,0])# 生成相同维度的随机矩阵
        pick_random =(random_numbers < self.epsilon).long()# 如果小于epsilon
        random_actions = Categorical(avail_actions.float()).sample().long()# 把可选的动作进行类别分布# pick_random==1 说明 random_numbers < self.epsilon 进行随机探索# pick_random==0 说明 random_numbers > self.epsilon 选择动作价值最大的函数

        picked_actions = pick_random * random_actions +(1- pick_random)* masked_q_values.max(dim=2)[1]# 进行动作选择return picked_actions  # 选择的动作

计算单个智能体估计的Q值

# Calculate estimated Q-Values 得到每个agent对应的Q值
mac_out =[]
self.mac.init_hidden(batch.batch_size)for t inrange(batch.max_seq_length):
    agent_outs = self.mac.forward(batch, t=t)#计算智能体的Q值，获得Q表
    mac_out.append(agent_outs)#添加到列表中
mac_out = th.stack(mac_out, dim=1)# Concat over time 沿着维度1，连接张量 ([mac_out, 1])# Pick the Q-Values for the actions taken by each agent# 取每个agent动作对应的Q值，并且把最后不需要的一维去掉，因为最后一维只有一个值了
chosen_action_qvals = th.gather(mac_out[:,:-1], dim=3, index=actions).squeeze(3)# Remove the last dim

x_mac_out = mac_out.clone().detach()#提取数据不带梯度
x_mac_out[avail_actions ==0]=-9999999#不能执行的动作赋值为负无穷
max_action_qvals, max_action_index = x_mac_out[:,:-1].max(dim=3)#最大的动作值及其索引

max_action_index = max_action_index.detach().unsqueeze(3)#去掉梯度
is_max_action =(max_action_index == actions).int().float()#是最大动作

计算单个智能体目标Q值

# Calculate the Q-Values necessary for the target 计算目标Q值
target_mac_out =[]
self.target_mac.init_hidden(batch.batch_size)#初始化隐层 RNNAgentfor t inrange(batch.max_seq_length):
    target_agent_outs = self.target_mac.forward(batch, t=t)#计算Q值，获得Q表
    target_mac_out.append(target_agent_outs)#添加到列表中# We don't need the first timesteps Q-Value estimate for calculating targets
target_mac_out = th.stack(target_mac_out[1:], dim=1)# Concat across time# Max over target Q-Values 找到最大的动作价值if self.args.double_q:#是否使用double q# Get actions that maximise live Q (for double q-learning)
    mac_out_detach = mac_out.clone().detach()#去掉梯度
    mac_out_detach[avail_actions ==0]=-9999999#不能执行的动作赋值为负无穷
    cur_max_actions = mac_out_detach[:,1:].max(dim=3, keepdim=True)[1]#找到最大价值的动作# 利用最优动作求取最大动作价值，并且把最后不需要的一维去掉
    target_max_qvals = th.gather(target_mac_out,3, cur_max_actions).squeeze(3)else:
    target_max_qvals = target_mac_out.max(dim=3)[0]#找到最大价值函数

根据损失函数，进行反向传播

# Mix 混合网络，求total值# qmix更新过程，evaluate网络输入的是每个agent选出来的行为的q值，target网络输入的是每个agent最大的q值，和DQN更新方式一样if self.mixer isnotNone:
    chosen_action_qvals = self.mixer(chosen_action_qvals, batch["state"][:,:-1])# 计算Q _{ tot }(evalutate)
    target_max_qvals = self.target_mixer(target_max_qvals, batch["state"][:,1:])# 计算Q _{ tot }(target )# Calculate 1-step Q-Learning targets 以Q-Learning的方法计算目标值r+gamma*Q _{ tot }({ target }
targets = rewards + self.args.gamma *(1- terminated)* target_max_qvals

# Td-error
td_error =(chosen_action_qvals - targets.detach())

mask = mask.expand_as(td_error)# 将mask扩展为td_error相同的size# 0-out the targets that came from padded data
masked_td_error = td_error * mask  # 抹掉填充的经验的td_error# Normal L2 loss, take mean over actual data# L2的损失函数，不能直接用mean，因为还有许多经验是没用的，所以要求和再比真实的经验数，才是真正的均值
loss =(masked_td_error **2).sum()/ mask.sum()# Optimise# 优化
self.optimiser.zero_grad()# 梯度清零
loss.backward()# 反向传播
grad_norm = th.nn.utils.clip_grad_norm_(self.params, self.args.grad_norm_clip)# 梯度剪裁
self.optimiser.step()# 执行# 在指定周期更新 target network 的参数if(episode_num - self.last_target_update_episode)/ self.args.target_update_interval >=1.0:
    self._update_targets()
    self.last_target_update_episode = episode_num

3 实验效果：

IQL、VDN和QMIX在StarCraft II六种不同的战斗地图上的获胜率。基于启发式的算法的性能用虚线表示。

参考：

博客：【QMIX】一种基于Value-Based多智能体算法
   多智能体强化学习入门（五）——QMIX算法分析
   多智能体强化学习入门Qmix
代码：https://github.com/wjh720/QPLEX