前言
📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。
🚀对毕设有任何疑问都可以问学长哦!
选题指导: https://blog.csdn.net/qq_37340229/article/details/128243277
大家好,这里是海浪学长毕设专题,本次分享的课题是
🎯基于 MATLAB 的小波去噪的研究
课题背景和意义
近些年来,小波分析理论发展得十分迅速,良 好的时域和频域特性使得其广泛地被应用于实际。 在现实中,搜集到的信号往往都是含有噪声的,噪 声的存在常常会将原始信号所要表达的信息掩盖 掉,所以,在实际对信号的处理过程中,降噪是首 先要进行的,并且是非常重要的一个步骤。 小波分析法去噪是当前广泛应用的信号去噪 方法,小波分析法源于傅里叶变换,却相比传统的 傅里叶分析去噪而言,更适合于对非平稳信号的去 噪问题。傅里叶分析去噪适合于平稳信号去噪,可 是生活中非平稳信号是绝大部分的,因此使用傅里 叶分析法来去噪就存在着局限性。多分辨率分析 是小波分析的特点,并且无论在时域还是频域内, 均具有表征信号局部特征的能力。因此,在去噪 领域中,小波理论受到了广泛的关注,并取得了不 错的效果。 小波分析去噪的核心环节包括小波基函数的 选择,阈值函数的选择、分解的层数等,小波包相 对于小波分析对于高频的刻画更为精细,小波包去 噪也被用于信号的去噪。
实现技术思路
一、小波理论
小波变换
设ψ ( t ) ∈ L 2( R) ,其傅里叶变换为 ψˆ (ω ) ,当ψ ω 满足条件:
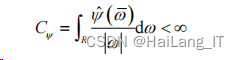
把 ψ (t) 称作基本小波(或母小波),将母小波 ψ (t) 经过伸缩和平移后即可得到一个小波序列为:
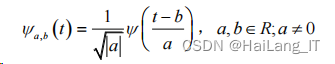
式中: *a *为伸缩因子; *b *为平移因子。
对于任意的函数 f( t) ∈L 2(R) 的连续的小波 变换为:
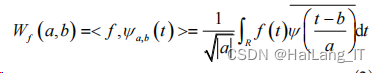
其重构公式(即小波逆变换)为:
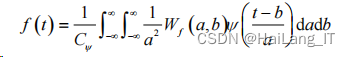
**几种常见的小波基 **
小波基选取是小波分析去噪的关键环节之一,选择合适的小波基作为小波分析的基函数,能够使
小波去噪取得不错的效果。以下为几种常见的小波基函数。
(1)Haar 小波系
Haar 小波的定义为:
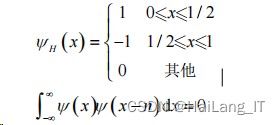
Haar 小波系为 A. Haar 提出的一种正交的函数系,此小波系具备紧支撑性,并且在正交的函数系
中是属于最简单的一种
(2)Daubechies(dbN)小波系
Daubechies(dbN)小波函数也是由Daubechies构造的小波函数,是从两尺度方程系数{h**k}出发而设
计的离散正交小波函数。
(3)SymletsA(symN)小波系
SymletsA 函数为一种近似对称的,紧支集、双正交特性小波函数系,为 db 小波函数的一种改进,
此 SymletsA 函数一般表示为 symN 的形式,其中N=2,3,4,5,6,7,8。
(4)Coiflet(coifN)小波系 Coiflet 小波基具有紧支撑正交特性,是由 Daubechies 构造的小波函数, 函数有 coifN (N=1, 2,3,4,5)这一系列,Coiflet 小波基比 dbN 小波 基对称性更好,而且 coifN 与 db3N、sym3N 具有相 同的支撑长度,与 db2N、sym2N 具有相同的消失 矩数目
**小波包理论 **
小波变换是一种将时域分析、频域分析联系在一起的分析方法,多分辨率分析法是将信号分解为
高频部分和低频部分的分析方法,可是,通常是将低频部分保留下来,而对于高频部分的分析处理往往不知所措
二、小波去噪原理
**小波分析去噪原理 **
小波去噪一般分为染噪信号的分解、阈值的处理、信号的重构 3 个步骤。
(1)信号的分解:选取小波基对染噪的信号进行小波变换。
(2)阈值的处理:事先设定一个阈值,然后将比设定阈值低的小波系数去掉,保留比设定阈值高的小波系数,从而可以将噪声去除,保留住有用信号的信息。
(3)信号的重构:用处理后的小波系数进行信号重构。
**阈值去噪 **
模极大值法、空域相关法、小波阈值法是小波滤波去噪的 3 种主要的方法,相比较于前 2 种滤波
方法,小波阈值法滤波具有算法简单、计算量小、滤波效果好等特点,对于信噪比低的信号的处理也比较适用。
小波阈值去噪通常可以分为硬阈值去噪及软阈值去噪 2 种。
Donoho 提出的硬阈值函数的数学表达式为:

软阈值的数学表达式为:
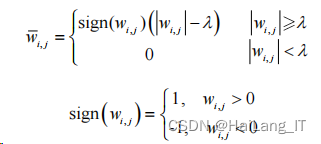
wi j 是去噪前的小波系数, , wi j 为去噪后的小波系数,阈值 λ =σ 2 lg(M ) ,M 为信 号长度,噪声水平的估计值
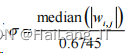
常见的阈值选择规则有以下 4 种:①固定阈值 sqtwolog 规则,阈值 λ=2In(M);②启发式阈值 Heursure 规则,为最优预测变量阈值选择;③自适 应阈值选择 Rigruse 规则,此种规则是基于无偏估 计;④极大极小阈值 Minmaxi 规则,此规则也是一 种固定的阈值选择规则。
**小波包去噪 **
与小波分析去噪相比,小波包对信号的分解以及重构愈加精细,对低频部分以及高频部分均实施分解,因而具有更强、更精确的局部分析能力。 小波包阈值去噪的基本步骤如下:①对信号进 行小波包分解;②选择最优小波基;③小波包分解 系数的阈值化;④信号的小波包重构。
三、去噪实验仿真
不同小波基下信号去噪
本实验为仿真小波基函数选取、分解的层数、 阈值选取对小波分析最终去噪效果的影响。如图为原始信号以及加噪信号。

通过波形观察、各种方式滤波信噪比(SNR)、各种方式滤波最小均方根误差(MSE)2 个重要指标的对比,来衡量和评价滤波去噪效果,得到数据如表
3层分解的小波分析去噪:
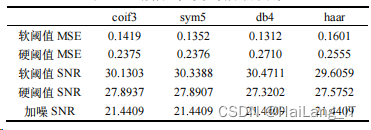
**5 **层分解的小波分析去噪:
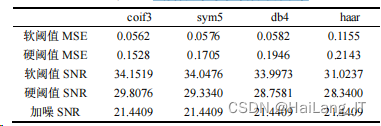
通过 4 种小波基去噪结果的数据对比可以发 现,coif3、sym5、db4 3 种小波基情况下的滤波效 果要好于 haar 小波基情况。coif3 小波基、sym5 小 波基处理噪声效果比 db4 小波基略好。因此,小波 基的选择不唯一,没有一种小波基对任何一种信号 去噪都能取得最优的效果。所以,实际去噪时,应 根据具体情况来选择适合的小波基函数对小波进 行分解。
下图分别为不同小波基情况下的去噪波形图
**haar **小波基分解的小波去噪:

**coif3 **小波基分解的小波去噪:
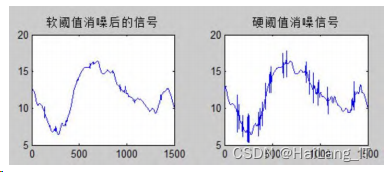
**db4 **小波基下的小波去噪
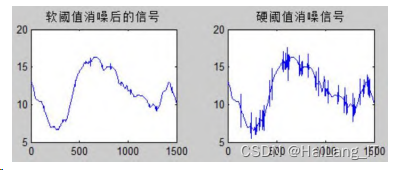
从中可以发现 coif3、sym5、db4 3 种小波基下 的去噪效果要好于 haar 小波基情况。软阈值去噪效 果好于硬阈值,去噪之后跟原信号更接近。但是 haar 小波基特更适合于连续性较差的信号的小波去噪, 比如 block 信号。coif3、sym5 更适合于连续性较好 的信号的去噪,比如 Doppler 信号的去噪。
**小波去噪与傅里叶分析去噪效果比较 **
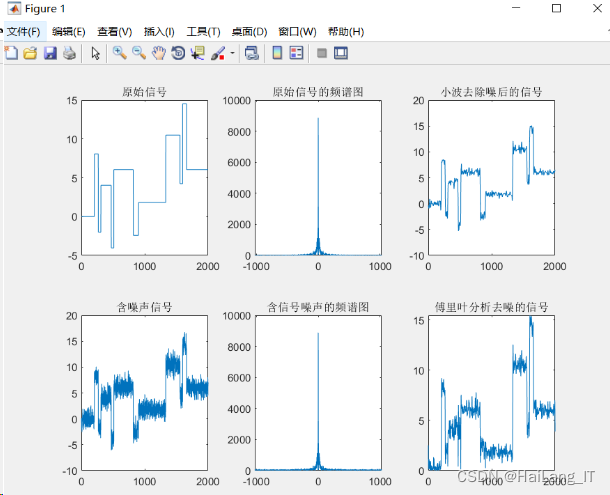
首先,产生测试信号—Doppler 信号,Doppler信号为一种非平稳信号,加入白噪声,得到原始信
号和染噪信号如图
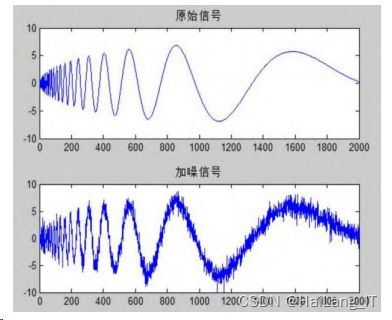
由图可知小波分析去噪结果好于傅里叶分析去噪。在非平稳信号的去噪方面,小波分析去噪相 对于傅里叶分析具有很大的优势,并且在实际工程应用中,大多数的信号也都为非平稳信号

**小波包去噪 **
1、分解层数对去噪效果的影响
产生 bumps 测试信号,然后高斯白噪声加入 bumps 信号,得到原始信号及加噪信号如图所示。
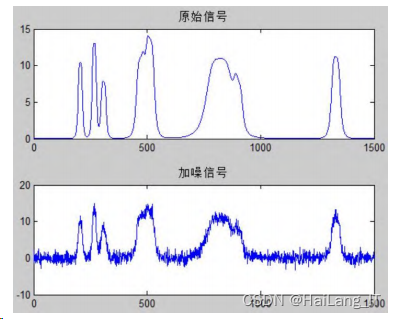
然后运用小波包分析对染噪信号进行去噪处理,实 验中,小波包分解层数分别设置为 2 层、4 层、5 层、8 层,得到去噪后信号波形如图

2、小波包与小波分析去噪比较
先产生 quadchirp 测试信号,然后将高斯白噪声加入 quadchirp,得到原始信号及加噪信号的波形
如图
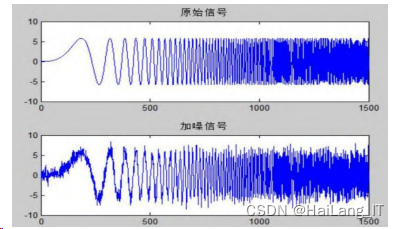
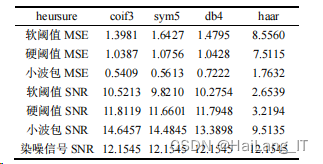
小波包去噪方法采用软阈值去噪,4 层分解;小波分析去噪,阈值选择采用最优预测变量阈值 heursure,分别采用软阈值和硬阈值 2 种方式,分解层数为 4 层。实验分别选用 coif3、sym5、db4、haar4 种小波基作为小波分解的基函数。仿真结果如图
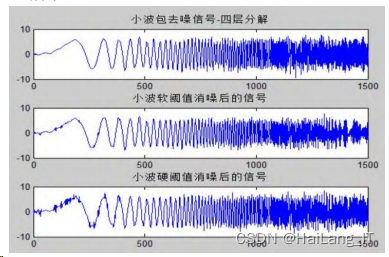
表为小波包去噪和小波去噪的结果数据,通 过表可以发现,小波包去噪相比较小波硬阈值去 噪、小波软阈值去噪具有更高的信噪比 SNR 和更低 的最小均方误差 MSE,表明对于 quadchirp 信号而 言,小波包去噪的效果要优于小波分析去噪。
实现效果图样例
matlab信号处理,小波降噪:
我是海浪学长,创作不易,欢迎点赞、关注、收藏、留言。
毕设帮助,疑难解答,欢迎打扰!
最后
版权归原作者 HaiLang_IT 所有, 如有侵权,请联系我们删除。