随着深度学习的发展，越来越多的模型诞生，并且在训练集和测试集上的表现甚至于高于人类，但是深度学习一直被认为是一个黑盒模型，我们通俗的认为，经过训练后，机器学习到了数据中的特征，进而可以正确的预测结果，但是，对于机器到底学到了什么，仍然是个黑盒模型，我们迫切想要知道机器所学习到的特征，这就需要对模型的可解释性进行研究。
本文主要介绍一下机器学习可解释性的相关内容与实现方法，并回答以下问题。
- 什么是机器学习可解释性？
- 为什么要进行可解释性的研究
- Lime可解释性的原理
- Lime可解释性的代码实现
什么是机器学习可解释性？
对于机器学习的用户而言，模型的可解释性是一种较为主观的性质，我们无法通过严谨的数学表达方法形式化定义可解释性。通常，我们可以认为机器学习的可解释性刻画了“人类对模型决策或预测结果的理解程度”，即用户可以更容易地理解解释性较高的模型做出的决策和预测。
从哲学的角度来说，为了理解何为机器学习的可解释性，我们需要回答以下几个问题：首先，我们应该如何定义对模型的“解释”，怎样的解释才足够好？许多学者认为，要判断一个解释是否足够好，取决于这个解释需要回答的问题是什么。对于机器学习任务而言，我们最感兴趣的两类问题是“为什么会得到该结果”和“为什么结果应该是这样”。而理想状态下，如果我们能够通过溯因推理的方式恢复出模型计算出输出结果的过程，就可以实现较强的模型解释性。
实际上，我们可以从“可解释性”和“完整性”这两个方面来衡量一种解释是否合理。“可解释性”旨在通过一种人类能够理解的方式描述系统的内部结构，它与人类的认知、知识和偏见息息相关；而“完整性”旨在通过一种精确的方式来描述系统的各个操作步骤（例如，剖析深度学习网络中的数学操作和参数）。然而，不幸的是，我们很难同时实现很强的“可解释性”和“完整性”，这是因为精确的解释术语往往对于人们来说晦涩难懂。同时，仅仅使用人类能够理解的方式进行解释由往往会引入人类认知上的偏见。
此外，我们还可以从更宏大的角度理解“可解释性人工智能”，将其作为一个“人与智能体的交互”问题。如图 1所示，人与智能体的交互涉及人工智能、社会科学、人机交互等领域。
为什么要进行可解释性的研究
在当下的深度学习浪潮中，许多新发表的工作都声称自己可以在目标任务上取得良好的性能。尽管如此，用户在诸如医疗、法律、金融等应用场景下仍然需要从更为详细和具象的角度理解得出结论的原因。为模型赋予较强的可解释性也有利于确保其公平性、隐私保护性能、鲁棒性，说明输入到输出之间个状态的因果关系，提升用户对产品的信任程度。下面，我们从“完善深度学习模型”、“深度学习模型与人的关系”、“深度学习模型与社会的关系”3 个方面简介研究机器学习可解释性的意义。
（1）完善深度学习模型
大多数深度学习模型是由数据驱动的黑盒模型，而这些模型本身成为了知识的来源，模型能提取到怎样的知识在很大程度上依赖于模型的组织架构、对数据的表征方式，对模型的可解释性可以显式地捕获这些知识。
尽管深度学习模型可以取得优异的性能，但是由于我们难以对深度学习模型进行调试，使其质量保证工作难以实现。对错误结果的解释可以为修复系统提供指导。
（2）深度学习模型与人的关系
在人与深度学习模型交互的过程中，会形成经过组织的知识结构来为用户解释模型复杂的工作机制，即「心理模型」。为了让用户得到更好的交互体验，满足其好奇心，就需要赋予模型较强的可解释性，否则用户会感到沮丧，失去对模型的信任和使用兴趣。
人们希望协调自身的知识结构要素之间的矛盾或不一致性。如果机器做出了与人的意愿有出入的决策，用户则会试图解释这种差异。当机器的决策对人的生活影响越大时，对于这种决策的解释就更为重要。
当模型的决策和预测结果对用户的生活会产生重要影响时，对模型的可解释性与用户对模型的信任程度息息相关。例如，对于医疗、自动驾驶等与人们的生命健康紧密相关的任务，以及保险、金融、理财、法律等与用户财产安全相关的任务，用户往往需要模型具有很强的可解释性才会谨慎地采用该模型。
（3）深度学习模型与社会的关系
由于深度学习高度依赖于训练数据，而训练数据往往并不是无偏的，会产生对于人种、性别、职业等因素的偏见。为了保证模型的公平性，用户会要求深度学习模型具有检测偏见的功能，能够通过对自身决策的解释说明其公平。
深度学习模型作为一种商品具有很强的社会交互属性，具有强可解释性的模型也会具有较高的社会认可度，会更容易被公众所接纳。
Lime可解释性的原理
Lime（Local Interpretable Model-Agnostic Explanations）是使用训练的局部代理模型来对单个样本进行解释。假设对于需要解释的黑盒模型，取关注的实例样本，在其附近进行扰动生成新的样本点，并得到黑盒模型的预测值，使用新的数据集训练可解释的模型（如线性回归、决策树），得到对黑盒模型良好的局部近似。值得注意的是，可解释性模型是黑盒模型的局部近似，而不是全局近似。
实现步骤
- 如上图是一个非线性的复杂模型，蓝/粉背景的交界为决策函数；
- 选取关注的样本点，如图粗线的红色十字叉为关注的样本点X；
- 定义一个相似度计算方式，以及要选取的K个特征来解释；
- 在该样本点周围进行扰动采样（细线的红色十字叉），按照它们到X的距离赋予样本权重；
- 用原模型对这些样本进行预测，并训练一个线性模型（虚线）在X的附近对原模型近似。 其数学表示如下：
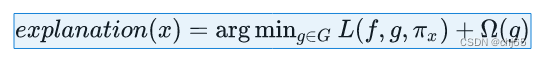对于实例x的解释模型g，我们通过最小化损失函数来比较模型g和原模型f的近似性，其中，代表了解释模型g的模型复杂度，G表示所有可能的解释模型（例如我们想用线性模型解释，则G表示所有的线性模型），定义了x的邻域。我们通过最小化L使得模型f变得可解释。其中，模型g，邻域范围大小，模型复杂度均需要定义。
对于结构化数据，首先确定可解释性模型，兴趣点x，邻域的范围。LIME首先在全局进行采样，然后对于所有采样点，选出兴趣点x的邻域，然后利用兴趣点的邻域范围拟合可解释性模型。如图。
其中，背景灰色为负例，背景蓝色为正例，黄色为兴趣点，小粒度黑色点为采样点，大粒度黑点为邻域范围，右下图为LIME的结果。
LIME的优点我们很容易就可以看到，原理简单，适用范围广，可解释任何黑箱模型。
Lime可解释性的代码实现
算法流程
宏观来看：
首先，在待解释的模型中取一个待解释样本，之后随机生成扰动样本，并以与待解释样本的距离作为标准附加权重，再将得到的结果作为输入投入待解释模型中，同时选择在局部考察的待训练可解释模型（如决策树、逻辑回归等等），最终即可训练出在可解释特征维度上的可解释性模型。
微观来看：
选取待解释样本X，并转换为可解释特征维度上的样本X’。
通过随机扰动，得到其余在可解释特征维度上的样本Z’。
将Z’恢复至原始维度，计算f（z）与相似度。
利用自适应相似度对各个样本点进行加权。
以X’作为特征，f（z）作为标准训练局部可解释模型（如图虚线）。
import sklearn
import sklearn.datasets
import sklearn.ensemble
import numpy as np
import lime
import lime.lime_tabular
#读取数据
x = np.array(data[feats].fillna(-99999))
y = np.array(data['target'])# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state =400)# 以XGBoost模型为例
model_xgb = xgb.XGBClassifier(
learning_rate =0.05,
n_estimators=50,
max_depth=3,
min_child_weight=1,
gamma=0.3,
subsample=0.8,
colsample_bytree=0.8,
objective='multi:softprob',
nthread=4,
scale_pos_weight=1,
num_class=2,
seed=27).fit(X_train, y_train)# 生成解释器
explainer = lime.lime_tabular.LimeTabularExplainer(X_train, feature_names=feats,
class_names=[0,1], discretize_continuous=True)# 对局部点的解释
i = np.random.randint(0, X_test.shape[0])#参数解释#image:待解释图像#classifier_fn:分类器#labels:可解析标签#hide_color:隐藏颜色#top_labels:预测概率最高的K个标签生成解释#num_features:说明中出现的最大功能数#num_samples:学习线性模型的邻域大小#batch_size:批处理大小#distance_metric:距离度量#model_regressor:模型回归器，默认为岭回归#segmentation_fn:分段，将图像分为多个大小#random_seed:随机整数，用作分割算法的随机种子
exp = explainer.explain_instance(X_test[i], model_xgb.predict_proba, num_features=6)# 显示详细信息图
exp.show_in_notebook(show_table=True, show_all=True)# 显示权重图
exp.as_pyplot_figure()
结果示例：
版权归原作者 chj65 所有， 如有侵权，请联系我们删除。