基于主成分分析的LSTM和GPR融合负荷预测
** **一、背景介绍
二、部分代码展示
三、结果分析
一、背景介绍
本文数据来源于某地区2020年1月1日至12月31日的综合能源系统冷热电负荷和其他各种影响因子,每间隔一小时采一次样。本文先利用主成分分析对原数据进行降维,再利用改进的双向Bi-LSTM网络对训练集样本进行训练,然后将待预测的输入样本用训练好的网络进行预测得到基于过去和未来共同影响的点预测值;再将上述点预测值作为GPR的输入进行再预测,此时Bi-LSTM网络得到的预测值可以看作是真实值带上了适宜程度的随机噪声,这样就提高了GPR模型的泛化能力和容错率。但很多时候我们需要的不仅仅是一个具体的值,一个给定置信度的范围往往更具有实际意义也更能令人接受。因此再设置显著性水平为5%,通过训练好的GPR模型得到相应的预测区间。最后再对点预测值进一步优化,将Bi-LSTM和GPR得到的点预测值进行线性赋权融合进一步降低预测误差从而得到最终的结果。
二、部分代码展示
1、数据预处理部分
%% *导入数据*
a = load("所有数据(文本格式).txt"); %载入原数据集
%% *异常值剔除*
outliers = isoutlier(a); %离群值检测
outliers_index = find(outliers); %存储离群值下标
a = filloutliers(a,'next'); %使用后一个相邻的数据填充离群值
%% *划分训练集和测试集*
train_input = a(1:floor(0.75*numel(a(:,1))),2:end);
train_output = a(1:floor(0.75*numel(a(:,1))),1);
validate_input = a(floor(0.75*numel(a(:,1)))+1:end,2:end);
%% *数据标准化*
[train_input,mu1,sigma1] = zscore(train_input);%输入数据标准化
[train_output,mu2,sigma2] = zscore(train_output);%输出数据标准化
validate_input = (validate_input-mu1)./sigma1;
注:这里先对训练集进行标准化处理,再利用训练集的标准化设置对测试集数据标准化,这样可以将待预测的新数据用训练好的模型进行预测
2、评估指标部分
%%
% 计算误差
MAE = sum(abs(Pre_data3-a(:,1)))/length(a(:,1));
disp('平均绝对误差为');
disp(MAE);
MRE = sum(abs(Pre_data3-a(:,1))./a(:,1))/length(a(:,1));
disp('平均相对误差为');
disp(MRE);
MSE = sum((Pre_data3-a(:,1)).^2)/length(a(:,1));
disp('均方误差为');
disp(MSE);
RMSE = sqrt(MSE);
disp('均方根误差为');
disp(RMSE);
三、结果分析
1、主成分分析

前三个主成分的双标图
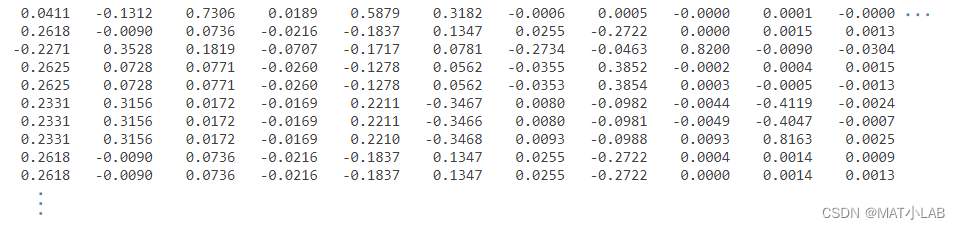
载荷矩阵(每一列是一个主成分,每一行是一个特征因子)
结合载荷矩阵和双标图分析,取前三个主成分(累积方差贡献率已超过85%)中绝对载荷之和较大(这里是取和大于0.4的特征)的特征作为待分析的特征因子,其余特征舍去,由于特征中含有线性相关的项,因此载荷相同的特征只选取其中一个即可(例如特征4和特征5的载荷都是0.2625,0.0728,0.0771),所以只选取特征4进行后续处理。
2、Bi-LSTM分析
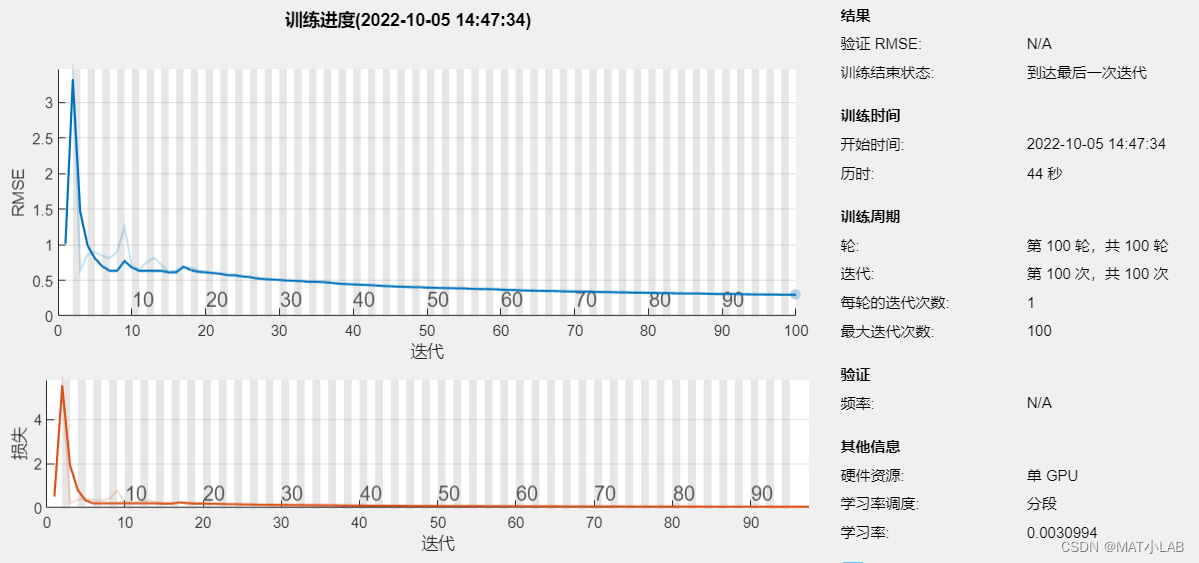
Bi-LSTM网络的训练进度
这里采用了自适应调节学习率来训练网络,初始学习率设置的是0.008,训练结束时为0.003,通过衰减学习率可以使网络更好地收敛在最优区域附近。
3、GPR分析

GPR预测结果
这里为了使图像更好分辨一些,只选取训练集的倒数前20个数据和预测集的前10个数据进行绘图展示。受上个网络产生的噪声影响可以使GPR模型的泛化能力更强,从图中看效果还是非常不错的。
4、模型融合分析

各模型预测结果对比图
在得出了置信区间后,我们再将Bi-LSTM和GPR各自得到的预测值进行一个线性的赋权融合,使其残差的平方和最小,采用最小二乘法得出各模型的权重,并绘制图像。
5、评估指标分析

评估指标
最后,得到评估指标值如图所示,可以看出预测的效果还是令人满意的。
注:需要数据集和源代码的请私信 (请说明缘由,否则本人不会处理)
版权归原作者 MAT小LAB 所有, 如有侵权,请联系我们删除。