如何检测时间序列中的异方差（Heteroskedasticity）

时间序列中非恒定方差的检测与处理，如果一个时间序列的方差随时间变化，那么它就是异方差的。否则数据集是同方差的。

异方差性影响时间序列建模。因此检测和处理这种情况非常重要。

让我们从一个可视化的例子开始。

下面的图1显示了航空公司乘客的时间序列。可以看到在整个序列中变化是不同的。在该系列的后一部分方差更高。这也是数据水平跨度比前面的数据大。

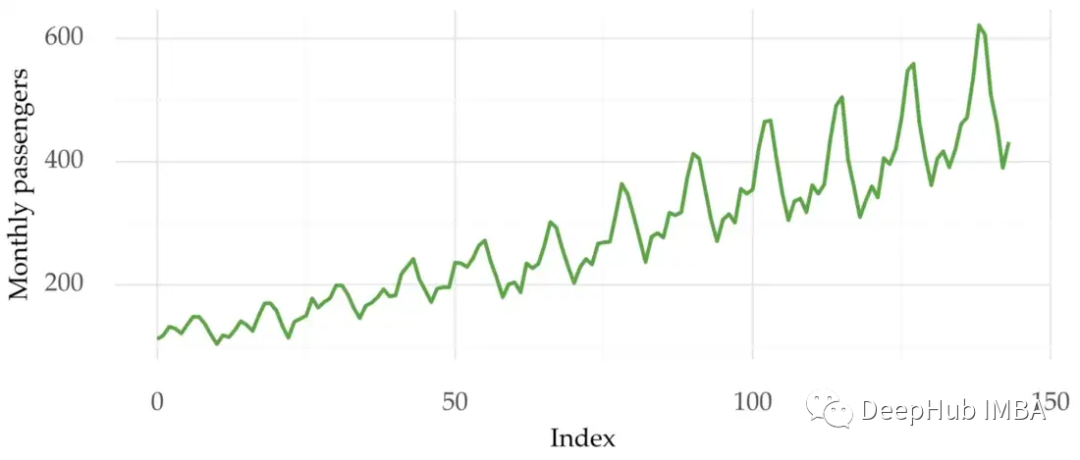
方差的变化对预测会产生很大的影响。它会影响模型的拟合从而影响预测性能。但是只靠人眼查看方差是不现实的，所以如何更系统地检测和处理异方差问题呢?

检测异方差性

你可以使用统计检验来检查时间序列是否为异方差序列。其中包括以下内容。

White 检验;

Breusch-Pagan检验;

Goldfeld-Quandt检验

这些检验的主要输入是回归模型的残差(如普通最小二乘法)。零假设是残差的分布方差相等。如果p值小于显著性水平，则拒绝该假设。这就说明时间序列是异方差的，检验显著性水平通常设置为0.05。

Python库statsmodels实现了上述三个测试。下面的代码片段将它们封装在一个类中:

 import pandas as pd
 import statsmodels.stats.api as sms
 from statsmodels.formula.api import ols
 
 TEST_NAMES = ['White', 'Breusch-Pagan', 'Goldfeld-Quandt']
 FORMULA = 'value ~ time'
 
 
 class Heteroskedasticity:
 
     @staticmethod
     def het_tests(series: pd.Series, test: str) -> float:
         """
         Testing for heteroskedasticity
 
         :param series: Univariate time series as pd.Series
         :param test: String denoting the test. One of 'white','goldfeldquandt', or 'breuschpagan'
 
         :return: p-value as a float.
 
         If the p-value is high, we accept the null hypothesis that the data is homoskedastic
         """
         assert test in TEST_NAMES, 'Unknown test'
 
         series = series.reset_index(drop=True).reset_index()
         series.columns = ['time', 'value']
         series['time'] += 1
 
         olsr = ols(FORMULA, series).fit()
 
         if test == 'White':
             _, p_value, _, _ = sms.het_white(olsr.resid, olsr.model.exog)
         elif test == 'Goldfeld-Quandt':
             _, p_value, _ = sms.het_goldfeldquandt(olsr.resid, olsr.model.exog, alternative='two-sided')
         else:
             _, p_value, _, _ = sms.het_breuschpagan(olsr.resid, olsr.model.exog)
 
         return p_value
 
     @classmethod
     def run_all_tests(cls, series: pd.Series):
 
         test_results = {k: cls.het_tests(series, k) for k in TEST_NAMES}
 
         return test_results

异方差类包含两个函数：het_tests函数应用特定的检验(White、Breusch-Pagan或Goldfeld-Quandt)。run_all_tests函数一次性应用所有三个检验。这些函数的输出是相应测试的p值。

下面介绍如何将此代码应用于图1中的时间序列。

 from pmdarima.datasets import load_airpassengers
 
 # https://github.com/vcerqueira/blog/blob/main/src/heteroskedasticity.py
 from src.heteroskedasticity import Heteroskedasticity
 
 series = load_airpassengers(True)
 
 test_results = Heteroskedasticity.run_all_tests(series)
 
 # {'Breusch-Pagan': 4.55e-07,
 # 'Goldfeld-Quandt': 8.81e-13,
 # 'White': 4.34e-07}

所有检验的p值都接近于零。所以我们可以拒绝零假设。这些试验为异方差的存在提供了令人信服的证据。

为了再次证明我们的观点，我们可以将时间序列前半部分和后半部分方差的分布进行可视化:

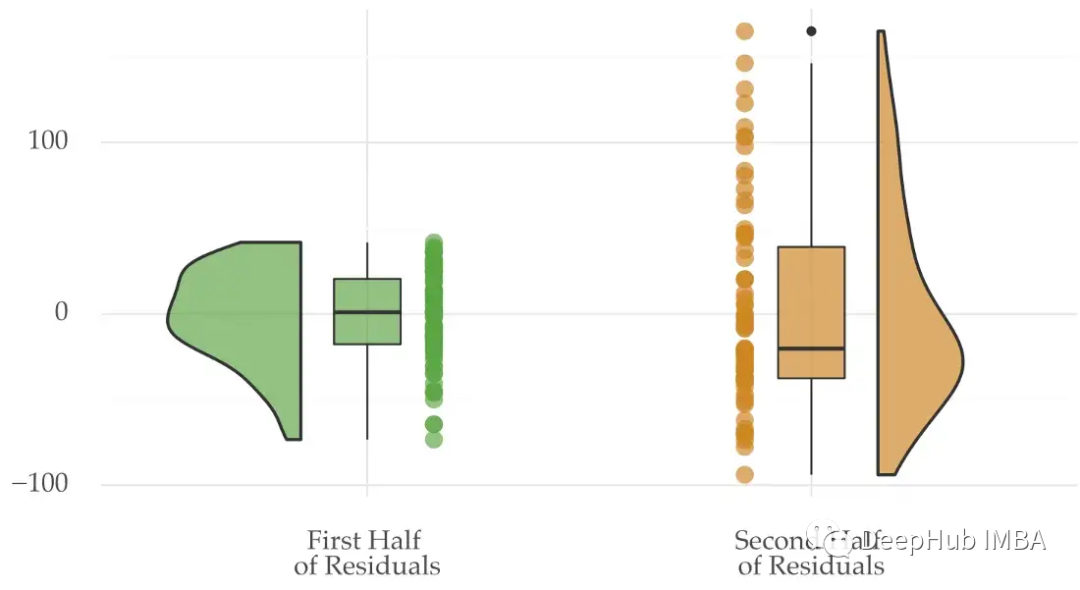
这两部分的方差分布不同。Goldfeld-Quandt检验就是使用这种类型的数据分折来检验异方差性。它检查两个数据子样本的残差方差是否不同。

数据转换

解决时间序列异方差问题的一个常用方法是对数据进行变换。对时间序列取对数有助于稳定其可变性。

下面是与之前相同的时间序列，但对其进行了对数缩放:

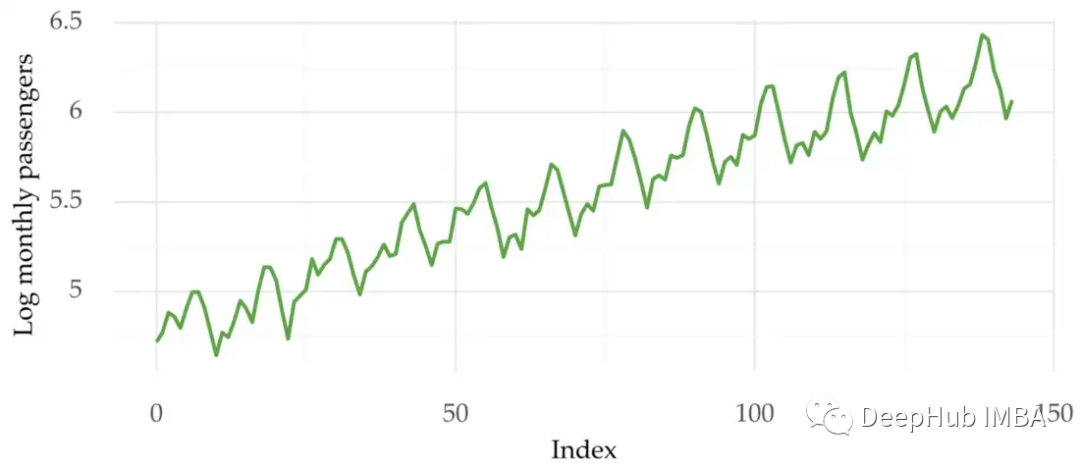
序列看起来很稳定。我们对新的序列重新进行检验

 import numpy as np
 
 test_results = Heteroskedasticity.run_all_tests(np.log(series))
 
 # {'Breusch-Pagan': 0.033,
 # 'Goldfeld-Quandt': 0.18,
 # 'White': 0.10}

可以看到这次的p值更大。只有一个检验(Breusch-Pagan)拒绝了零假设（这里假设显著性水平为0.05）。

恢复对数缩放转换

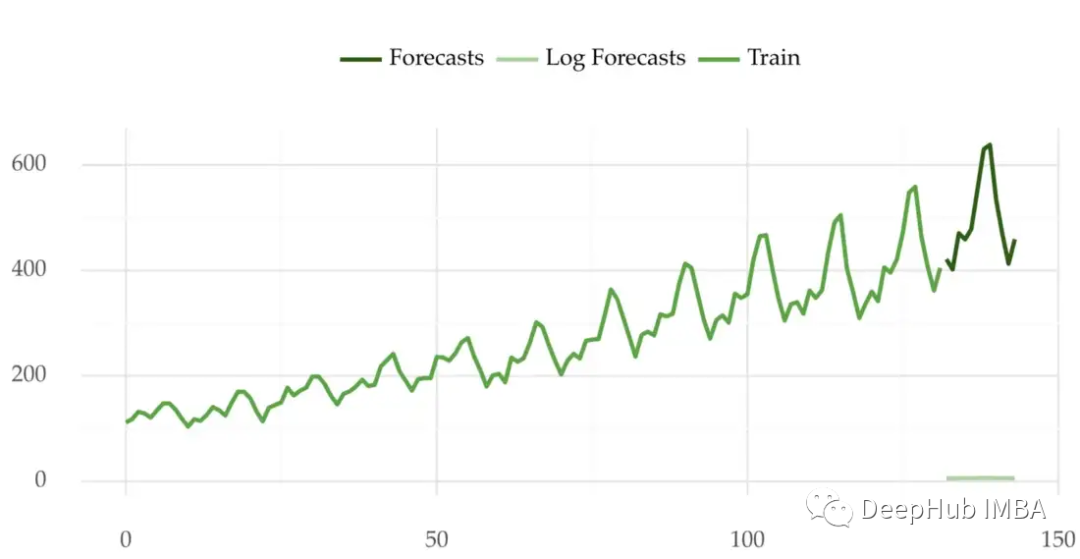
我们使用对数变换后的数据进行预测，预测结果还是需要还原到原始尺度的。这是通过逆变换来完成的，在对数的情况下，你应该使用指数变换。

所以我们的完整预测过程的如下:

对数据进行变换，使方差稳定;

拟合预测模型;

获得预测结果，并将其恢复到原始尺度。

代码如下：

 import numpy as np
 from pmdarima.datasets import load_airpassengers
 from pmdarima.arima import auto_arima
 from sklearn.model_selection import train_test_split
 
 series = load_airpassengers(True)
 
 # leaving the last 12 points for testing
 train, test = train_test_split(series, test_size=12, shuffle=False)
 # stabilizing the variance in the train
 log_train = np.log(train)
 
 # building an arima model, m is the seasonal period (monthly)
 mod = auto_arima(log_train, seasonal=True, m=12)
 
 # getting the log forecasts
 log_forecasts = mod.predict(12)
 
 # reverting the forecasts
 forecasts = np.exp(log_forecasts)

总结

本文的重点内容总结如下：

• 如果方差不是恒定的则时间序列是异方差的;
• 可以使用统计检验来检验一个时间序列是否为异方差序列。这些测试包括White，Breusch-Pagan，Goldfeld-Quandt检验;
• 使用对数变换来稳定方差;
• 预测值需要还原到原始值。

作者：Vitor Cerqueira