【机器学习】决策树-Gini指数

1. CART树

    分类回归树(CART,Classification And Regression Tree)算法是一种决策树分类方法。CART每一个节点上都采用二分法，采用一种二分递归分割的技术，CART生成的树必须是二叉树，也就是无论回归还是分类，无论特征离散还是连续，无论属性取值有多个还是两个，内部节点只能根据属性进行二分。因此，CART算法生成的决策树是结构简洁的二叉树。  CART算法既可以用分类任务，也可用于回归任务。

1-2 回归树

 CART作为回归树：使用**平方误差**最小准则来选择特征并进行划分，也叫最小二乘回归树。对于特征*j*，找到j所有的划分点*s，s*将数据集分为*c1、c2*两部分，找出使得两部分的方差最小，同时整体方差最小的特征j以及划分点*s*。对于离散特征，采用均值或者中位数作为节点的输出结果。

1-3 分类树

 CART作为分类树：使用**Gini指数**最小化准则来选择特征并进行划分。

1-4 终止条件

 CART算法构建二叉树 终止条件：

    1、所有叶节点样本数为1，或属于同一类，或小于某一阈值；

    2、树的高度到达某一阈值；

    3、无剩余属性。

2. 基尼指与基尼指数

**2-1 基尼值 **

    **基尼值**可用来度量数据集的纯度，数据集D的基尼系数Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，因此Gini(D)越小，则数据集D的纯度越高。pk表示选中的样本属于k类别的概率，则这个样本被分错的概率是(1-pk)

2-2 基尼指数

** 基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。**
Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。 即 基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率。

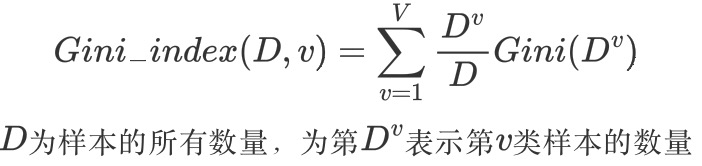
     对于特征A，若其将数据集分为D1和D2两部分，则其基尼指数为：

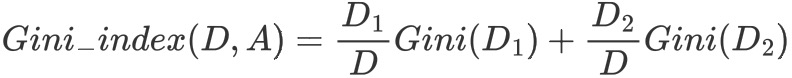
    在候选集中，选择那个使得划分后基尼指数最小的属性作为最优的划分属性。

2-3 案例

1. 1. 案例根据'有房者'、'婚姻'、'年收入'三个特征判断是否回拖欠贷款。2. 根据gini指数构建cart分类树的过程如下：

3.总结

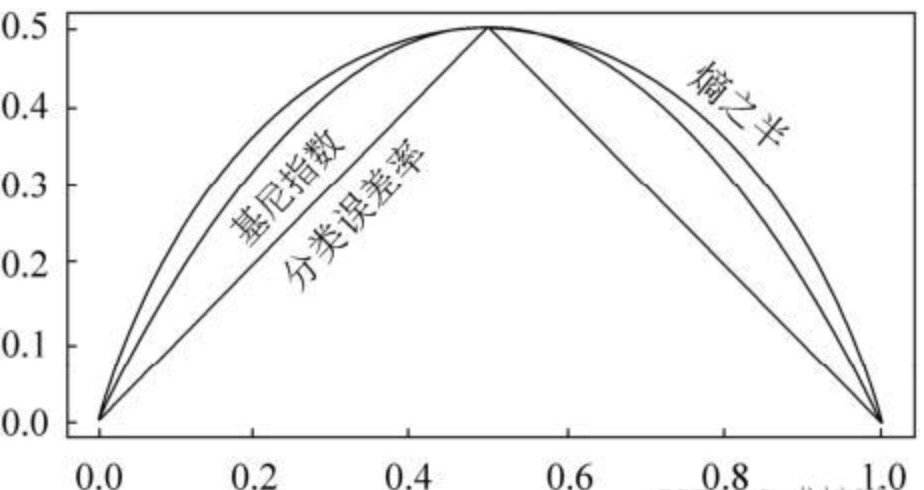
    基尼系数也是一种衡量信息不确定性的方法，与信息熵计算出来的结果差距很小，基本可以忽略，但是基尼系数要计算快得多，因为没有对数。熵和基尼指数的关系如下图：

Reference：

     1.

https://www.cnblogs.com/yuyingblogs/p/15319571.html