目录
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖,由本人亲自从底层编写、测试与文章配套的各个经典算法,不依赖于现有库,可以大大加深对算法的理解。
🚀详情:机器学习强基计划(附几十种经典模型源码)
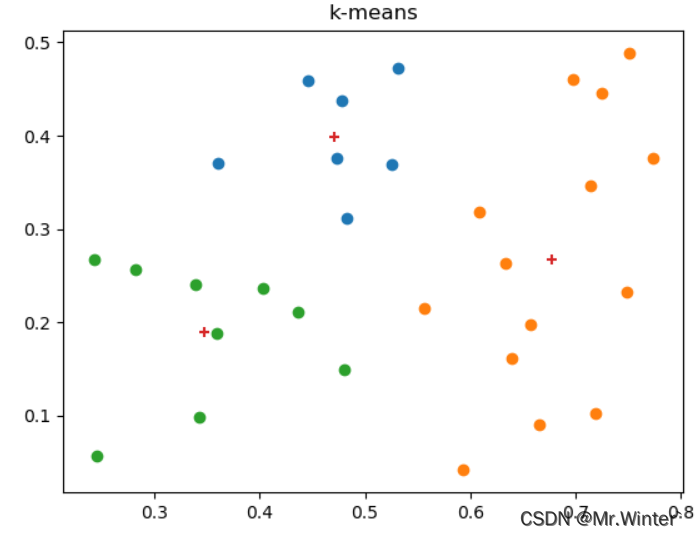
本文的目标是基于K-均值聚类原理实现下面的可视化效果
1 什么是聚类?
聚类(clustering)是无监督学习(unsupervised learning)中研究最多、应用最广的技术之一,其基本思路是通过对无标记训练样本的学习来揭示数据内在的聚合性质与规律。
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个**簇(cluster)**,每个簇可能对应于一些潜在的概念(类别),但这些概念的语义需由开发者来把握和命名。
形式化地,假定训练集
X
=
{
x
1
,
x
2
,
⋯
,
x
m
}
X=\left\{ \boldsymbol{x}_1,\boldsymbol{x}_2,\cdots ,\boldsymbol{x}_m \right\}
X={x1,x2,⋯,xm}包含
m
m
m个无标记样本,每个样本
x
i
=
{
x
i
1
,
x
i
2
,
⋯
,
x
i
n
}
\boldsymbol{x}_i=\left\{ x_{i1},x_{i2},\cdots ,x_{in} \right\}
xi={xi1,xi2,⋯,xin}是一个
n
n
n维征向量。
聚类算法的目标是将训练集
X
X
X划分为
k
k
k个不相交的簇
C
=
{
C
1
,
C
2
,
⋯
,
C
k
}
\mathcal{C} =\left\{ C_1,C_2,\cdots ,C_k \right\}
C={C1,C2,⋯,Ck},其中
C
l
′
∩
C
l
=
⊘
C_{l'}\cap C_l=\oslash
Cl′∩Cl=⊘且
X
=
⋃
l
=
1
k
C
l
X=\bigcup\nolimits_{l=1}^k{C_l}
X=⋃l=1kCl,每个簇都对应一个未赋语义的**簇标记(cluster label)**,记为
λ
j
∈
{
1
,
2
,
⋯
,
k
}
\lambda _j\in \left\{ 1,2,\cdots ,k \right\}
λj∈{1,2,⋯,k},聚类的结果可用包含
m
m
m个元素的簇标记向量表示
λ
=
[
λ
1
λ
2
⋯
λ
m
]
T
\boldsymbol{\lambda }=\left[ \begin{matrix} \lambda _1& \lambda _2& \cdots& \lambda _m\\\end{matrix} \right] ^T
λ=[λ1λ2⋯λm]T。
聚类既能作为一个单独过程,用于找寻数据内在的聚合结构,也可作为分类等其他学习任务的前驱过程。
例1 在一些商业应用中需对用户类型进行判别,但商家往往不知道用户可以分为哪些类型,此时可先对用户数据集进行聚类,根据聚类结果将每个簇定义为一种类型用户,然后再基于这些类训练分类模型,用于判别新用户的类型。
2 K均值聚类原理
2.1 原型聚类
原型聚类(prototype-based clustering)的核心原理是通过参考原型向量(模板向量)或原型分布(模板分布)的方式来完成聚类过程。
在学得一组原型向量
{
p
1
,
p
2
,
⋯
,
p
k
}
\left\{ \boldsymbol{p}_1,\boldsymbol{p}_2,\cdots ,\boldsymbol{p}_k \right\}
{p1,p2,⋯,pk}后即可实现对样本空间的簇划分。对任意样本
x
\boldsymbol{x}
x ,将被划入与其距离最近的原型向量
p
i
\boldsymbol{p}_i
pi所代表的簇中,该样本与
p
i
\boldsymbol{p}_i
pi的距离不大于它与其他原型向量的距离。
2.2 K-means算法流程
**K-均值聚类(K-means)**属于原型聚类的一种,它以簇均值向量为模板向量,通过贪心策略迭代划分簇。算法流程如下

3 Python实现
3.1 算法复现
- 初始化均值向量
self.kVector =[copy.deepcopy(self.dataSet[random.randint(0, self.m -1)])for i inrange(self.k)] - 更新簇划分
t =0while t < self.T:# 初始化簇 kCluster ={i:[]for i inrange(self.k)}# 更新簇划分for i inrange(self.m):# 样本与各均值向量的距离 d =[self.__dist(self.dataSet[i], self.kVector[j])for j inrange(self.k)]# 以最小距离对应的簇号为簇标记 label = d.index(min(d))# 更新簇划分 kCluster[label].append(self.dataSet[i]) - 更新均值向量
# 更新均值向量kVectorNew =[sum(kCluster[i])/len(kCluster[i])for i inrange(self.k)]# 计算均值向量更新幅度delta =[sum(kVectorNew[i]- self.kVector[i])for i inrange(self.k)]ifsum(delta)<0.01:breakelse: self.kVector = kVectorNewt = t +1
3.2 可视化
for i in kCluster:
x = np.array(kCluster[i])[:,0]
y = np.array(kCluster[i])[:,1]
plt.scatter(x,y)# 绘制均值向量点的位置
xMean = np.array(self.kVector)[:,0]
yMean = np.array(self.kVector)[:,1]
plt.scatter(xMean, yMean, marker='+')
plt.title("k-means")
plt.show()
这里我们额外作出了均值向量的位置,用**+**表示。

可以验证,每个簇内样本到均值向量的距离都小于到其他簇均值向量的距离。
本文完整工程代码联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《机器人原理与技术》
- 《机器学习强基计划》
- 《计算机视觉教程》
- …
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇
版权归原作者 Mr.Winter` 所有, 如有侵权,请联系我们删除。