1 概述
CNN 的机理使得 CNN 在处理图像时可以做到 transition invariant,却没法做到 scaling invariant 和 rotation invariant。即使是现在火热的 transformer 搭建的图像模型 (swin transformer, vision transformer),也没办法做到这两点。(注:spatial transformer和这两个transformer原理不一样,虽然都叫transformer)因为他们在处理时都会参考图像中物体的相对大小和位置方向。不同大小和不同方向的物体,对网络来说是不同的东西。
其实 pooling layer 有一定程度上解决了这个问题,因为在做pooling 的时候,只要这个特征在,就可以提取出来,但池化层的感受野(receptive field)是固定(fixed)且局部(local)的,ST的行为取决于单个数据样本(意思是对于不同input image,ST的行为是随之改变的),因此是非局部的(non-locally)、动态的。
STN(spatial transformer network) 引入了一个新的可学习模块,空间变换器(ST),它可以对网络内的数据进行空间变换操作。
ST可以用反向传播机制(back-propagation,BP)进行端到端(end-to-end)训练。
这个可微模块可以插入到现有的卷积架构中,使神经网络能够以特征图本身为条件,主动地对特征图进行空间转换,而不需要任何额外的训练监督或对优化过程进行修改。
STN 能够在没有标注关键点的情况下,根据任务自己学习图片或特征的空间变换参数,将输入图片或者学习的特征在空间上进行对齐,从而减少物体由于空间中的旋转、平移、尺度、扭曲等几何变换对分类、定位等任务的影响。

a是输入图片,b 是 STN 中的 localisation 网络检测到的物体区域,c是 STN 对检测到的区域进行线性变换后输出,d 是有 STN 的分类网络的最终输出。
2 模型说明
STN(spatial transformer network) 更准确地说应该是 STL(spatial transformer layer),它就是网络中的一层,并且可以在任何两层之间添加一个或者多个。
如下图所示,spatial transformer 主要由两部分组成,分别是 localisation net 和 grid generator。
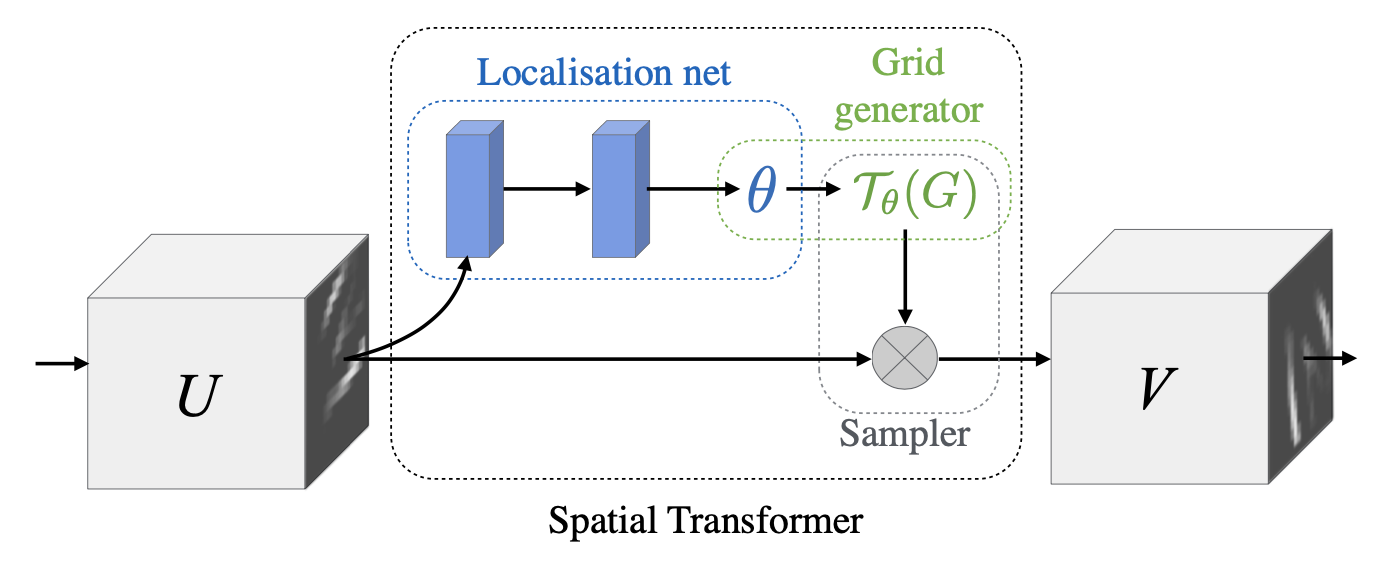
输入的特征图U被本地网络处理得到参数theta,然后经过网格生成器得到采样器,映射到原图U上,从而得到输出V。
2.1 Localisation Network
我们的目的是把第
l
−
1
l−1
l−1 层的第
n
n
n 行,第
m
m
m 列的特征移动到第
l
l
l层的某行某列。如下图 2-2 所示,一个
3
×
3
3 × 3
3×3 的特征要变换的话,第
l
l
l 层的每个位置都可以表示为
l
−
1
l-1
l−1 层的特征的加权和。通过控制权重 ,
w
n
m
,
i
j
l
w_{nm,ij}^l
wnm,ijl就可以实现任何仿射变换。
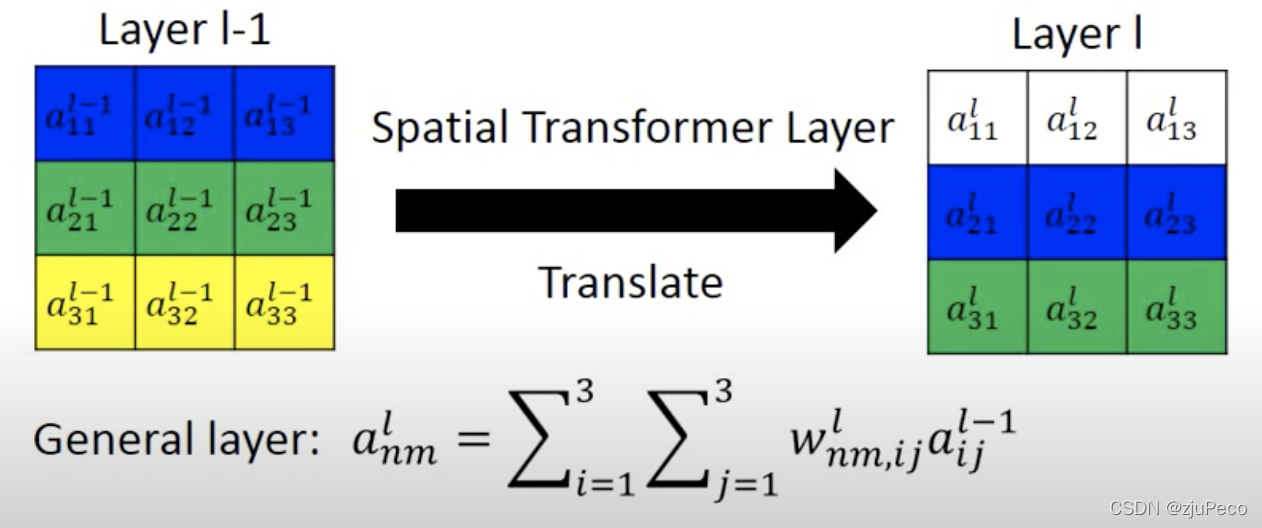
但如果直接加一层全连接让模型学的话,模型可能学出来的就不是仿射变换了,参数量也很大,很难学,很难控制。所有就设计了一个 localisation net,直接让模型学仿射变换的参数,这相当于是一个归纳偏置。
localisation net 的输入是前一层的特征,输出是仿射变换的参数,如果是平面的放射变换就是 6 个参数,通过这六个参数可以控制整个图像的平移,旋转,缩放。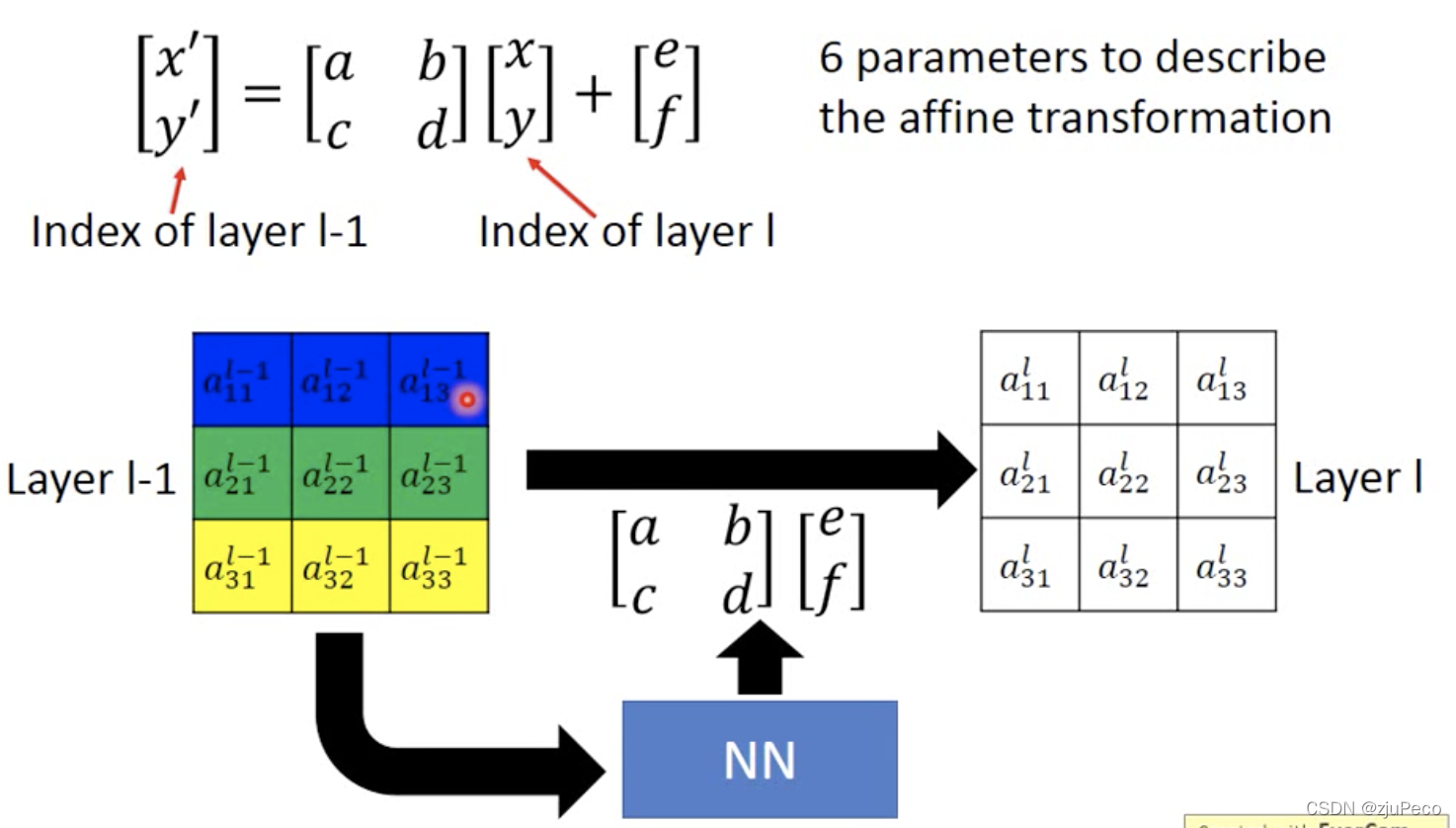
图 2-3 通过参数进行仿射变换示例
图 2-3 中的
[
a
,
b
,
c
,
d
,
e
,
f
]
[a,b,c,d,e,f]
[a,b,c,d,e,f]参数就是 localisation net 的输出。仿射变换公式就是
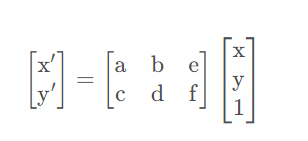
其中,
x
x
x 和
y
y
y 是当前层的坐标,
x
′
x′
x′ 和
y
′
y'
y′ 是前一层的坐标,
a
a
a 和
d
d
d 主要控制缩放,
b
b
b 和
c
c
c 主要控制旋转,
e
e
e 和
f
f
f 主要控制平移。
2.2 Parameterised Sampling Grid
localisation net 输出了仿射变换参数之后,仿射变换公式告诉了我们当前层
(
x
,
y
)
(x,y)
(x,y) 这个位置的特征是前一层的
(
x
′
,
y
′
)
(x', y')
(x′,y′) 位置的特征拿过来的。但是,如图 2-4 中的例子所示,
(
x
′
,
y
′
)
(x', y')
(x′,y′) 可能是小数,位置需要是正整数,如果采用取整的操作的话,网络就会变得不可梯度下降,没法更新参数了。
我们想要的是,当
[
a
,
b
,
c
,
d
,
e
,
f
]
[a,b,c,d,e,f]
[a,b,c,d,e,f] 发生微小的变化之后,下一层的特征也发生变化,这样才可以保证可以梯度下降。

图 2-4 带插值的仿射变换示意图
于是,作者就采用了插值的方法来进行采样。比如当坐标为
[
1.6
,
2.4
]
[1.6,2.4]
[1.6,2.4] 时,就用
[
a
12
l
−
1
,
a
13
l
−
1
,
a
22
l
−
1
,
a
23
l
−
1
]
[a_{12}^{l-1}, a_{13}^{l-1}, a_{22}^{l-1}, a_{23}^{l-1}]
[a12l−1,a13l−1,a22l−1,a23l−1]这几个值进行插值。这样一来
[
a
,
b
,
c
,
d
,
e
,
f
]
[a,b,c,d,e,f]
[a,b,c,d,e,f] 发生微小的变化之后,
[
x
,
y
]
[x,y]
[x,y] 位置采样得到的值也会有变化了。这也使得 spatial transformer 可以放到任何层,跟整个网络一起训练。
双线性插值的基本思想是通过某一点周围四个点的灰度值来估计出该点的灰度值,如图所示.
在实现时我们通常将变换后图像上所有的位置映射到原图像计算(这样做比正向计算方便得多),即依次遍历变换后图像上所有的像素点,根据仿射变换矩阵计算出映射到原图像上的坐标(可能出现小数),然后用双线性插值,根据该点周围 4 个位置的值加权平均得到该点值。过程可用如下公式表示: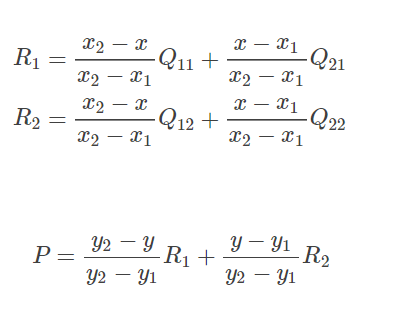
将 (11) 代入 (12) 整理得:
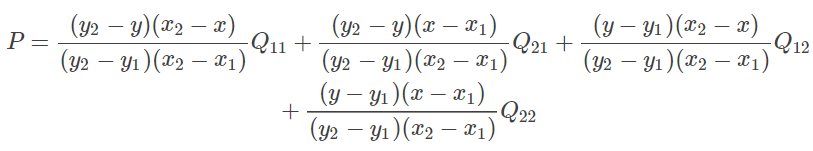
因为
Q
11
,
Q
12
,
Q
21
,
Q
22
Q11,Q12,Q21,Q22
Q11,Q12,Q21,Q22
是相邻的四个点,所以
y
2
−
y
1
=
1
,
x
2
−
x
1
=
1
y2−y1=1,x2−x1=1
y2−y1=1,x2−x1=1,则(13)可化简为:
P
=
(
y
2
−
y
)
(
x
2
−
x
)
Q
11
+
(
y
2
−
y
)
(
x
−
x
1
)
Q
21
+
(
y
−
y
1
)
(
x
2
−
x
)
Q
12
+
(
y
−
y
1
)
(
x
−
x
1
)
Q
22
P=(y_2-y)(x_2-x)Q_{11}+(y_2-y)(x-x_1)Q_{21}+(y-y_1)(x_2-x)Q_{12}+(y-y_1)(x-x_1) Q_{22}
P=(y2−y)(x2−x)Q11+(y2−y)(x−x1)Q21+(y−y1)(x2−x)Q12+(y−y1)(x−x1)Q22
版权归原作者 猛男技术控 所有, 如有侵权,请联系我们删除。
