1.历史
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,广泛应用在运筹学领域, 美国数学家哈罗德·库恩于1955年提出该算法,之所以被称作匈牙利算法是因为算法很大一部分是基于以前匈牙利数学家
Dénes Kőnig
(1884-1944)和
Jenő Egerváry
(1891-1958)的工作上创建起来的。
Kuhn H W. The Hungarian method for the assignment problem[J]. Naval research logistics quarterly, 1955, 2(1‐2): 83-97.
2.指派问题
匈牙利算法被用来求解任务分配问题,也叫指派问题,即
n
项任务,对应分配给
n
个人去做,应该由哪个人来完成哪项任务,能够使完成效率最高。

基于上图中的指派问题模型,匈牙利算法求解指派问题时的条件是,1)目标函数最小 2)人和任务数相同 3)效率非负,根据目标函数:
m
i
n
Z
=
∑
i
∑
j
c
i
j
x
i
j
min Z = \sum_{i} \sum_{j} c_{ij}x_{ij}
minZ=i∑j∑cijxij
匈牙利算法的目标,就是在变换系数矩阵中找到
n
个不同行不同列的
0
元素,以求解指派问题最优解。
现在借用一个例子来说明匈牙利算法的步骤。由一份说明书需要翻译成
ABCD
四种语言,现有
甲乙丙丁
四人去做四种语言的翻译所需要的时间见下表,需要求得的是如何指派任务使完成翻译工作需要的工时最少。

- 步骤1:系数矩阵在每行列上减去对应行列中的最小值,使各行各列都出现
0元素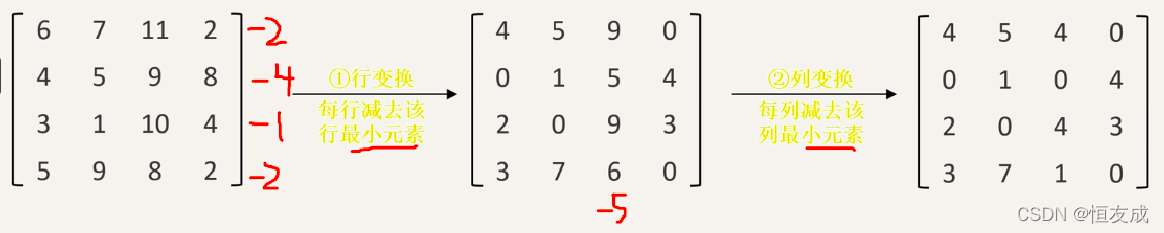
- 步骤2:试寻找指派最优解

- 步骤3:经过步骤2,第4行依然没有0元素,也就是丙这个人当前没有任务去做,第3步即增加矩阵中的
0元素,给丙分配任务
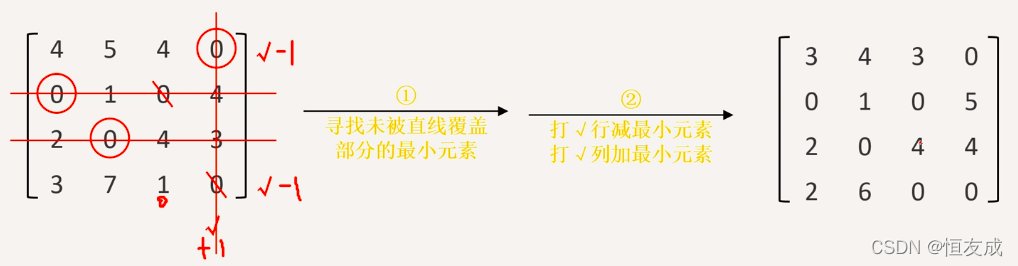
- 步骤4:重复步骤2、3,直到找到
n个位于不同行不同列的0元素,即最优解 - 最优解:
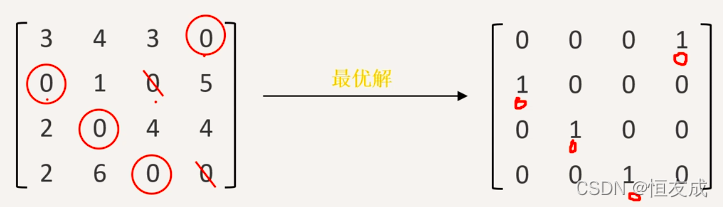
即最优方案为甲翻译D,乙翻译A,丙翻译B,丁翻译C
3.二部图与匈牙利算法
二部图(Bigraph, Bipartite graph)也被称做二分图,是一种特殊的图,其顶点可以分成两个不相交的集合(
U
和
V
),并且同属一个集合内的点两两不相连(
E
U
=
E
V
=
ϕ
E_U=E_V=\phi
EU=EV=ϕ,也就是说二分图中如有圈,则圈所包含的边的数量必定是偶数。
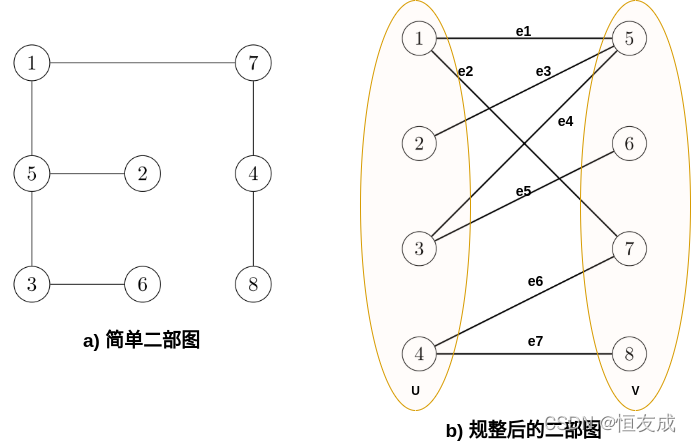
匹配:匹配(M)是定义为二部图中边的集合
M
⊂
E
M \subset E
M⊂E且其中任意两条边不共点即
∀
e
1
,
e
2
∈
M
,
s
.
t
.
e
1
∩
e
2
=
ϕ
\forall e_1,e_2\in M,s.t. e_1 \cap e_2 = \phi
∀e1,e2∈M,s.t.e1∩e2=ϕ
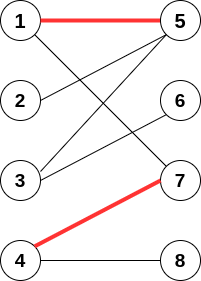
上图中红色的边{
e
1
,
e
6
e_1,e_6
e1,e6}组成的集合就是1个匹配,其他还可以定义各种匹配如{
e
5
e_5
e5}、{
e
2
e_2
e2,
e
5
e_5
e5}等,这些红色的边被称为**匹配边**,匹配边所连接的点被称为**匹配点**。同样可以定义**非匹配边**和**非匹配点**。
如果二分图里的某一个匹配包含的边的数量,在该二分图的所有匹配中最大,那么这个匹配称为**最大匹配(
Maximum Matching
)**
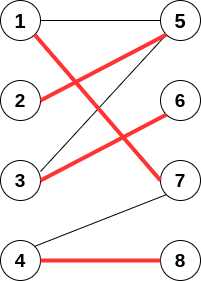
如上图就是1个最大匹配{
e
2
,
e
3
,
e
5
,
e
7
e_2,e_3,e_5,e_7
e2,e3,e5,e7}
交错路径:M是二部图G的一个匹配,G的一条M交错路径是指,其边在M和E(G)-M中交替出现的路径,如{
e
2
,
e
7
e_2,e_7
e2,e7}是一个匹配,则{
e
1
,
e
2
,
e
6
,
e
7
e_1,e_2,e_6,e_7
e1,e2,e6,e7}就是一条交错路径。
增广路径:在二分图的匹配中,如果一条路径的首尾是非匹配点,路径中除此之外(如果有)其他的点均是匹配点,那么这条路径就是一条增广路径(Agumenting path),从定义可知增广路径是一种特殊的交错路径。结合上面的图可知{
e
1
,
e
6
e_1,e_6
e1,e6}是匹配时,{
e
7
,
e
6
,
e
2
,
e
1
,
e
3
e_7,e_6,e_2,e_1,e_3
e7,e6,e2,e1,e3}是一条增广路径。
基于上述术语引出
Hall
定理,图G中的一个匹配M是最大匹配的充分必要条件是G中不存在M的增广路径。证明可参考
增广路径的首尾是非匹配点。因此,增广路径的第一条和最后一条边,必然是非匹配边;由交错路径的定义可知,增广路径从非匹配边开始,匹配边和非匹配边依次交替,最后由非匹配边结束。这样一来,增广路径中非匹配边的数目总比匹配边大 1。
考虑置换增广路径中的匹配边和非匹配边,由于增广路径的首尾是非匹配点,其余则是匹配点,这样的置换不会影响原匹配中其他的匹配边和匹配点,因而不会破坏匹配;而增广路径的置换,可使匹配的边数加1,得到比原有匹配更大的匹配。
由于二分图的最大匹配必然存在(比如,上限是包含所有顶点的完全匹配),所以,在任意匹配的基础上,如果有办法不断地搜寻出增广路径,直到最终我们找不到新的增广路径为止,就有可能得到二分图的一个最大匹配。匈牙利算法正是基于这种思想来实现的。
二部图的最大匹配可分成有权二部图和无权二部图,无权二部图的实例表示如宠物匹配,有权二部图实例如任务指派。
无权二部图的最大匹配不能使用贪心算法,可以使用网络流问题来进行求解。
有权二部图满足约束条件后可使用匈牙利算法来求最大匹配,两边的结点相同
∣
U
∣
=
∣
V
∣
=
n
|U|=|V|=n
∣U∣=∣V∣=n,匈牙利算法的时间复杂度为
O
(
n
3
)
O(n^3)
O(n3)。
4.在线工具及代码实现
- 可以输入系数矩阵,在线使用匈牙利算法来求解任务分配问题的一个网站
- 匈牙利算法的C++实现
1.https://www.bilibili.com/video/BV1hF411h7eX?spm_id_from=333.337.search-card.all.click
2.https://zh.wikipedia.org/wiki/%E5%8C%88%E7%89%99%E5%88%A9%E7%AE%97%E6%B3%95
3.https://www.zhihu.com/question/313845998
4.https://liam.page/2016/04/03/Hungarian-algorithm-in-the-maximum-matching-problem-of-bigraph/?utm_source=wechat_session&utm_medium=social&utm_oi=574981213526167552
5.https://www.youtube.com/watch?v=6DFWUgV5Osc&ab_channel=ShusenWang
版权归原作者 恒友成 所有, 如有侵权,请联系我们删除。