部分图片、数据、代码来源:https://book.tipdm.org/jc/220,侵权必删!!!
一、本篇主要介绍四种经典的时间序列模型
移动平均模型(MA)、自回归模型(AR)、自回归移动平均模型(ARMA)、整合移动平均自回归模型(ARIMA)。
二、序列的平稳性
平稳序列:样本时间序列所得到的拟合曲线在未来的一段期间内仍能顺着现有的形态“惯性”地延续下去。
不平稳序列:样本时间序列得到的拟合曲线在未来的一段期间内不再顺着现有的形态“惯性”延续下去。
序列的平稳性对处理序列时所用的方法模型有所不同,接下来介绍几种判断序列平稳性的方法。
1.图检验:可以使用python自带的绘图库绘制时序图,观察时序图的走势来判断其是否为稳定序列。常见的时序图类型如下:
白噪声序列:
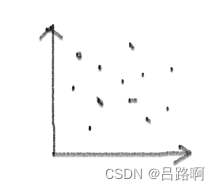 (黑点表示数据,横轴为时间,下同)
(黑点表示数据,横轴为时间,下同)
平稳非白噪声序列: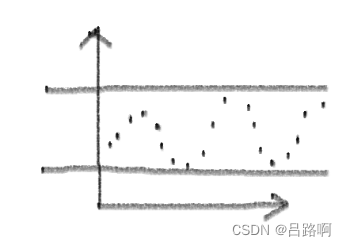
非平稳序列: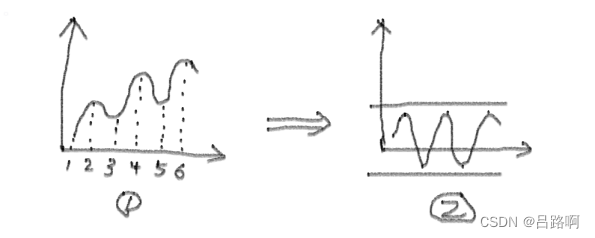
显然,①图不具有平稳性,但①图经过一阶差分后变为②图,即可将非平稳序列转化为平稳序列。在一些特殊情况下,通常需要多阶差分。
-----差分法介绍
①图中后一项与前一项的销售数量(t2-t1、t3-t2、…)差额作为②图的x轴,例如x1=t2-t1、x2=t3-t2、x3=t4-t3等等。显然,②图是①图的一阶差分后的图像。python中diff()函数用于作差分运算。
2.单位根检验(ADF)
图形检验法虽然很直观,但在检验过程中具有一定的主观性,识别精度不高,所以需要采用单位根检验法精确地判定时间序列的平稳性。ADF单位根检验可以通过python中的 statsmodels 模块,其中用到的函数是adfuller。若返回的p值小于0.05,则认为该序列为稳定序列。
from statsmodels.tsa.stattools import adfuller as ADF
三、对于不同的数据集,要使用合适的模型。
判断的依据主要为:时序图的走向、数据集的均值、方差、自相关系数(ACF)、偏自相关系数(PACF)。
1.自相关函数ACF(autocorrelation function)
自相关函数ACF描述的是时间序列观测值与其过去的观测值之间的线性相关性。
2.偏自相关函数PACF(partial autocorrelation function)
偏自相关函数PACF描述的是在给定中间观测值的条件下,时间序列观测值预期过去的观测值之间的线性相关性。
3.可以使用 绘制自相关图的函数plot_acf()和绘制偏自相关图的函数plot_pacf()画出自相关图和偏自相关图。
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
plot_acf(D_data)#画出自相关图# plt.show()
plot_pacf(D_data)#画出偏相关图# plt.show()
4.ACF和PACF主要呈现两种形式:拖尾和截尾。拖尾指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时点变得非常小。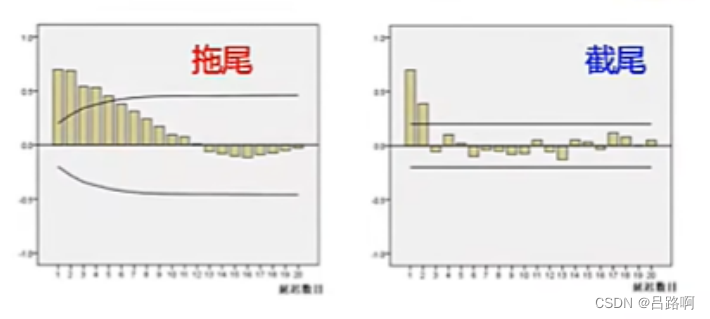
四、平稳非白噪声序列
1.自回归模型AR
自回归模型描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。
适用AR模型的数据需包含特点: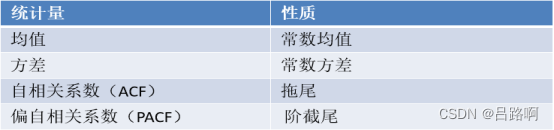
2.移动平均模型MA
适用MA模型的数据需包含特点: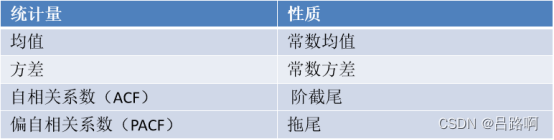
3.自回归移动平均模型ARMA(AR+MA)
自回归模型AR和移动平均模型MA模型相结合,我们就得到了自回归移动平均模型ARMA(p,q)
适用ARMA模型的数据需包含特点: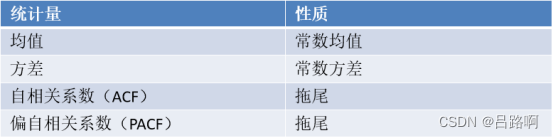
4.稳定时间序列的建模步骤: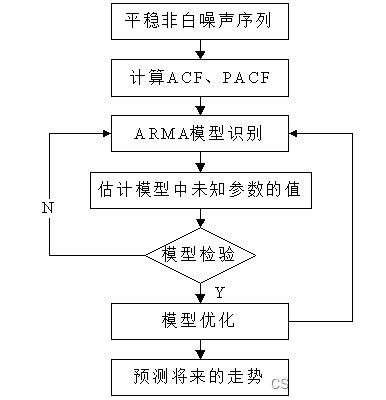
五、非平稳序列
差分平稳时间序列的ARIMA:将自回归模型、移动平均模型和差分法结合,就得到了差分自回归移动平均模型ARIMA(p,d,q),其中d是需要对数据进行差分的阶数。
模型建模步骤如下: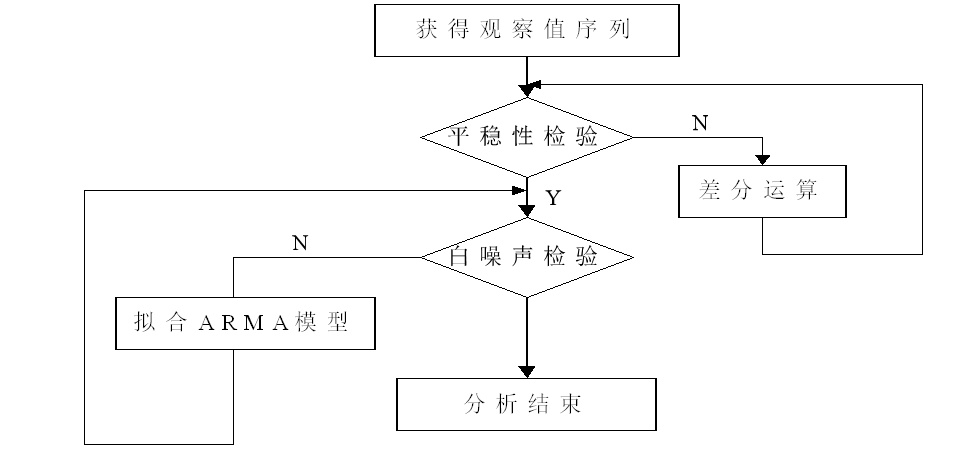
六、经过理论和建模步骤介绍之后,下面进入实战。
问题:对2015/1/1到2015/2/6某餐厅的销售数据进行建模预测其未来5天的销售情况。部分数据如下: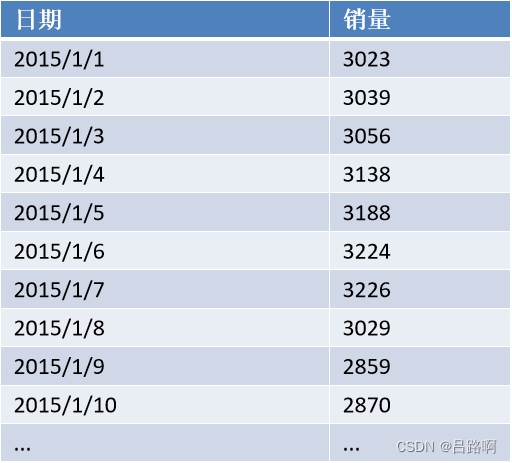
1.编写代码,读取excel表格中的数据。
import pandas as pd
discfile='D:\\01181756gtu3\\chapter5\\demo\\data\\arima_data.xls'
forecastunum=5# 读取数据,指定日期列为指标,pandas自动将“日期”列识别为Datetime格式
data=pd.read_excel(discfile,index_col='日期')
data
2.使用python自带的绘图库绘制时序图和自相关图,判断该序列的稳定性。
#绘制时序图import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']# 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False# 用来正常显示负号
data.plot()
plt.show()# 自相关图from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
时序图和自相关图结果如下: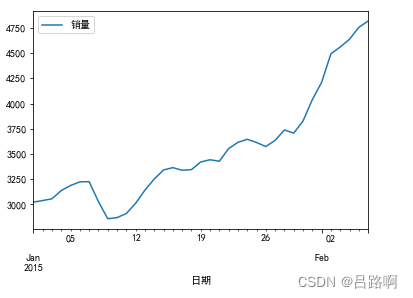
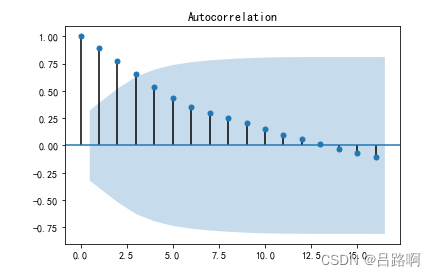
可以看出其是非稳定序列,需要使用ARIMA模型。依照ARIMA模型建模步骤,下一步需要将数据做差分。
3.对原始序列进行一阶差分,并进行平稳性和白噪声检验。
D_data = data.diff().dropna()#差分运算并删除空行
D_data.columns =['销量差分']
D_data.plot()# 时序图
plt.show()
plot_acf(D_data).show()# 自相关图from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show()# 偏自相关图print('差分序列的ADF检验结果为:', ADF(D_data['销量差分']))# 平稳性检测
# 白噪声检验from statsmodels.stats.diagnostic import acorr_ljungbox
print('差分序列的白噪声检验结果为:', acorr_ljungbox(D_data, lags=1))# 返回统计量和p值
结果显示,一阶差分之后的序列的时序图在均值附近比较平稳的波动、自相关图有很强的短期相关性、单位根检验p值小于0.05;所以一阶差分之后的序列是平稳序列。
4.对一阶差分之后的平稳非白噪声序列拟合ARMA模型
计算ARMA(p,q)当 p 和 q 均小于等于 3 的所有组合的 BIC 信息量,取其中 BIC 信息量达到最小的模型阶数。
其中arima为已经建立好的ARIMA模型,返回值是Model时序模型得到的AIC、BIC、HQIC指标值。
from statsmodels.tsa.arima_model import ARIMA
# 定阶
data['销量']= data['销量'].astype(float)
pmax =int(len(D_data)/10)# 一般阶数不超过length/10
qmax =int(len(D_data)/10)# 一般阶数不超过length/10
bic_matrix =[]# BIC矩阵for p inrange(pmax+1):
tmp =[]for q inrange(qmax+1):try:# 存在部分报错,所以用try来跳过报错。
tmp.append(ARIMA(data,(p,1,q)).fit().bic)except:
tmp.append(None)
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix)# 从中可以找出最小值
bic_matrix
输出BIC矩阵为: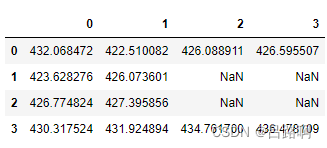
可以看出p值为1、q值为 0 时最小 BIC 值为:422.510082。
5.打印预测报告
model = ARIMA(data,(p,1,q)).fit()# 建立ARIMA(0, 1, 1)模型print('模型报告为:\n', model.summary2())print('预测未来5天,其预测结果、标准误差、置信区间如下:\n', model.forecast(5))
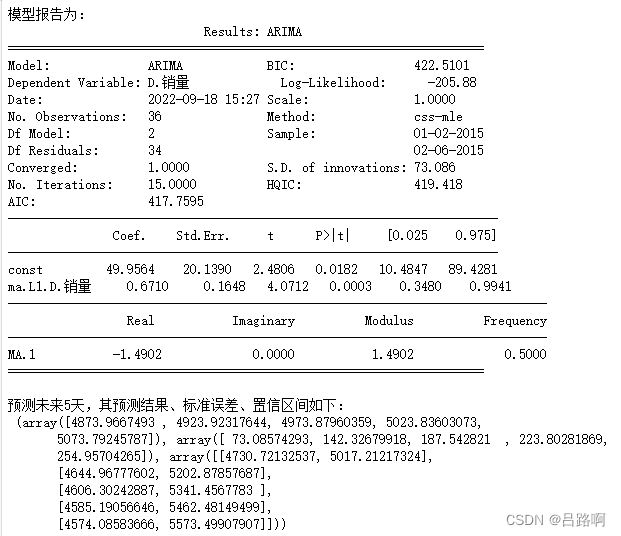
七、Python主要时序模式算法
在初学时,底层的数学公式看起来有点吓人,但python库中已经实现过了。只需学习模型框架,调用对应的方法即可解决问题。下面是对用到的方法的名称功能介绍。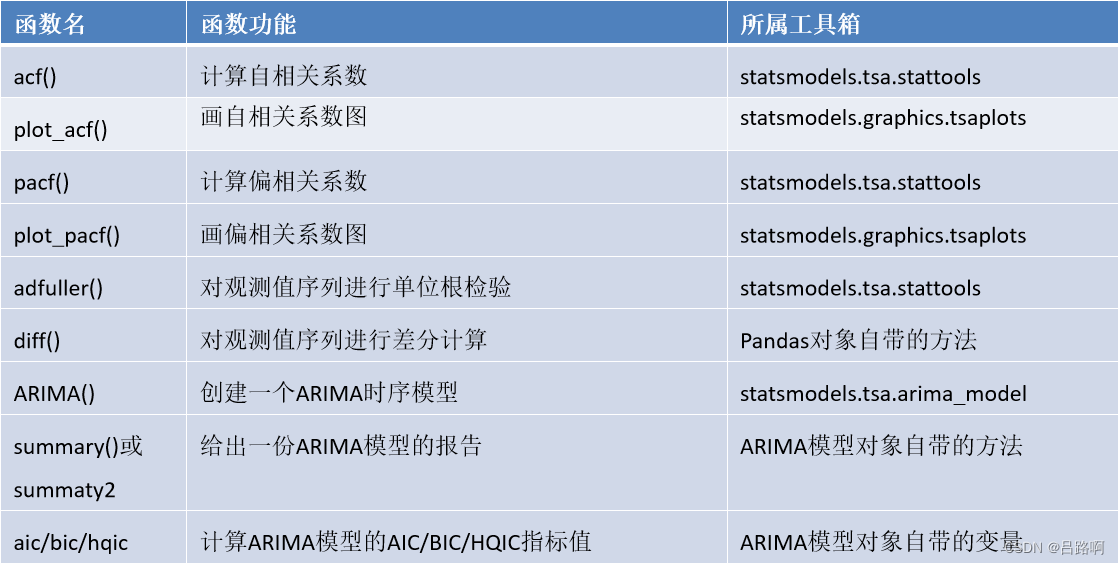

参考:https://book.tipdm.org/jc/220 第五章
参考:https://blog.csdn.net/weixin_33520805/article/details/113028670?spm=1001.2101.3001.6650.2&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-113028670-blog-88540034.pc_relevant_aa&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-113028670-blog-88540034.pc_relevant_aa&utm_relevant_index=5
版权归原作者 吕路啊 所有, 如有侵权,请联系我们删除。