孤立森林是 一种无监督算法的异常检测,可以快速检测数据集中的异常值。

孤立森林是一种简单但非常有效的算法,能够非常快速地发现数据集中的异常值。理解这个算法对于处理表格数据的数据科学家来说是必须的,所以在本文中将简要介绍算法背后的理论及其实现。
由于其算法非常的简单并且高效,所以 Scitkit Learn 已经将其进行了高效的实现,我们可以直接调用使用。但在直接进入示例之前,还是需要介绍其背后的理论,这样才可以深入的了解该算法的。
一些理论
1、什么是异常?
异常(异常值)可以描述为数据集中与其他数据或观察结果显著不同的数据点。发生这种情况的原因有几个:
- 异常值可能表示错误数据不正确或实验可能未正确运行。
- 异常值可能是由于随机变化或可能表明某些科学上有趣的东西。

2、为什么要进行异常检测?
我们之所以想要找出和深入研究异常,是因为这些数据点要么会浪费的时间和精力,要么可以让我们识别出有意义的东西。
在简单线性回归的情况下,错误的异常值会增加模型的方差,并进一步降低模型对数据的把握能力。异常值导致回归模型(尤其是线性模型)学习对异常值的偏差理解。
孤立森林如何工作
其他的方法一直在尝试构建正常数据的配置文件(分布、规律等),然后进一步将哪些不符合配置文件的数据点识别为异常。
而孤立森林的亮点在于它可以使用“孤立”规则来直接检测异常(一个数据点与其余数据的距离)。这意味着该算法可以像其他与距离相关的模型(例如 K-Nearest Neighbors)一样以线性时间复杂度运行。
该算法是通过以异常值最明显的特点为中心来进行工作:
- 只会有几个异常值
- 有异常值肯定与其他值不同
孤立森林通过引入(一组)二叉树来实现,该二叉树通过随机选择一个特征然后随机选择该特征的分割值来递归地生成分区。分区过程将一直持续,直到它将所有数据点与其余样本分开。
因为每棵树的实例中只选择一个特征。可以说决策树的最大深度实际上是一,所以孤立森林的基本估计器实际上是一个具有各种数据子集的极其随机的决策树(ExtraTrees)。
孤立森林中的一棵树的示例如下:
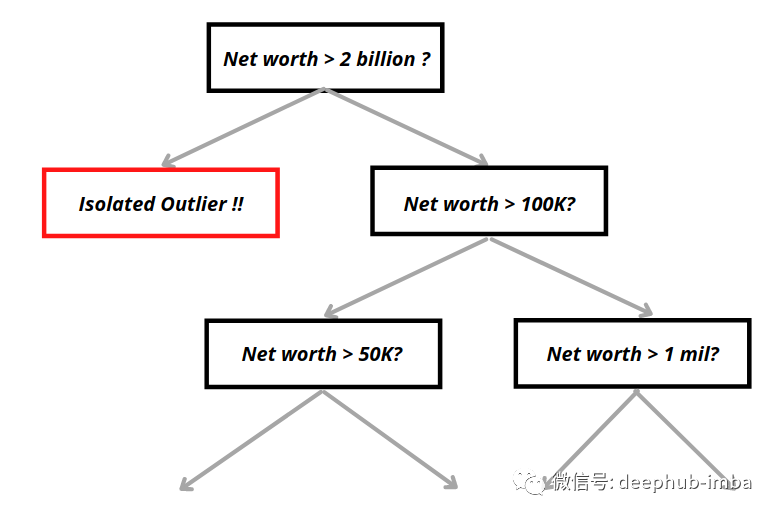
上图异常值的属性,可以观察到与正常样本相比异常值平均需要更少的分叉就能将它们隔离。每个数据点将在X轮之后根据它们被隔离的容易程度获得分数,有异常分数的数据点将被标记为异常。
通过随机选择属性q和分割值p(在属性q的最小最大值内)递归地分割每个数据实例,直到它们完全隔离。然后算法将提供一个排名,根据路径长度反映每个数据实例的异常程度。排名或分数称为异常分数,其计算方法如下:
- H(x):数据实例x完全隔离之前的步骤数。
- E[H(x)]:隔离树集合中H(x)的平均值。
这些度量是有意义的,但一个问题:树的最大可能步长为n阶,而平均步长仅为log n阶。这将导致步骤不能直接比较,所以需要引入一个由n变化的标准化常数 c(n),被称作路径长度归一化常数,公式如下:

其中 H (i) 是可以通过 ln (i) + 0.5772156649(欧拉常数)估计的谐波数。
异常分数的完整公式为:

因此,如果通过孤立森林运行整个数据集,就可以获得异常分数。使用异常分数 s,只要有异常分数非常接近 1 的实例,我们就可以推断存在在异常。或者说任何低于 0.5 的分数都将被识别为正常实例。
另外需要说明的是:在 sklearn 的实现中,异常分数与原始论文中定义的异常分数相反。它会减去常数 0.5。这是为了轻松识别异常(负分数与异常一起识别),具体可以参考sklearn文档
孤立森林示例
首先,我们快速导入一些有用包, 并使用 make_blob () 函数生成具有随机数据点的数据集。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
data, _ = make_blobs(n_samples=500, centers=1, cluster_std=2, center_box=(0, 0))
plt.scatter(data[:, 0], data[:, 1])
plt.show()

上图可以很容易地观察到一些异常值。这里我们使用二维用例是为快速证明算法有效性。该算法可以毫无问题地用于具有多维特征的数据集。
下面通过调用 IsolationForest() 来初始化一个孤立森林对象。
这里使用的超参数都是最默认的,也是原始论文推荐的。
树的数量控制集成的大小。路径长度通常会在 t = 100 之前收敛。除非另有说明,否则我们将在实验中使用 t = 100 作为默认值。
子集样本设置为 256 通常可以提供足够的细节来在广泛的数据中执行异常检测
N_estimators 代表树的数量,最大样本代表每轮使用的子集样本。
Max_samples = 'auto' 将子集大小设置为 min (256, num_samples)。
这里的contamination代表数据集中异常值的比例。默认情况下,异常分数阈值将遵循原始论文中的内容。但是,如果我们有任何先验知识,则可以手动设置数据中异常值的比例。本文中将其设置为 0.03。
拟合并预测整个数据集后会返回一个由 [-1 或 1] 组成的数组,其中 -1 代表异常,1 代表正常实例。
iforest = IsolationForest(n_estimators = 100, contamination = 0.03, max_samples ='auto)
prediction = iforest.fit_predict(data)
print(prediction[:20])
print("Number of outliers detected: {}".format(prediction[prediction < 0].sum()))
print("Number of normal samples detected: {}".format(prediction[prediction > 0].sum()))

然后我们将绘制隔检测到的异常值。
normal_data = data[np.where(prediction > 0)]
outliers = data[np.where(prediction < 0)]
plt.scatter(normal_data[:, 0], normal_data[:, 1])
plt.scatter(outliers[:, 0], outliers[:, 1])
plt.title("Random data points with outliers identified.")
plt.show()
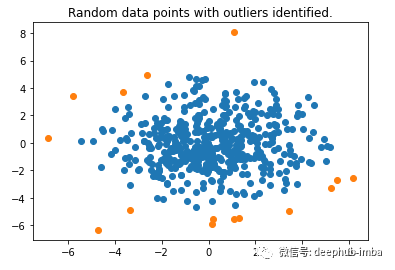
可以看到它工作得很好,可以识别边缘周围的数据点。
也可以调用decision_function()来计算每个数据点的异常分数。这样我们就可以了解哪些数据点比较异常。
score = iforest.decision_function(data)
data_scores = pd.DataFrame(list(zip(data[:, 0],data[:, 1],score)),columns = ['X','Y','Anomaly Score'])
display(data_scores.head())
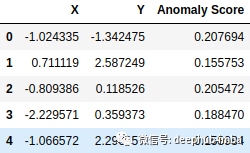
选择异常分数前 5 的异常值,然后再次绘制它。
top_5_outliers = data_scores.sort_values(by = ['Anomaly Score']).head()
plt.scatter(data[:, 0], data[:, 1])
plt.scatter(top_5_outliers['X'], top_5_outliers['Y'])
plt.title("Random data points with only 5 outliers identified.")
plt.show()

总结
孤立森林是一种完全不同的异常值检测模型,可以以极快的速度发现异常。它具有线性时间复杂度,这使其成为处理大量数据集的最佳方法之一。
它基于异常“很少且不同”这个概念,因此与正常点相比,异常点更容易被孤立。它的 Python 实现可以在 sklearn.ensemble.IsolationForest 找到。
论文地址:https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf?q=isolation-forest
Isolation Forest by Fei Tony Liu, Kai Ming Ting Gippsland School of Information Technology Monash University, Victoria, Australia.
作者:Yenwee Lim